ios 不被遮挡 阴影_理解微表面BRDF中的遮挡阴影函数（一）

学习几何函数的时候看到了毛神这篇【基于物理的渲染（PBR）白皮书】（五）几何函数相关总结，其中提到了2014年sig上《Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs》这篇文章对于遮挡阴影函数的发展起着非常重要的作用，因此小白我就去看了，完了之后看也没看懂，就打算一边看、一边翻译、一边找资料，肯定会有写的不对的地方，欢迎大家指正。当然如果只是简单了解的话强烈推荐大家直接去看毛神的那篇白皮书，因为这篇文章不会讲一些基础的东西，一些东西可能刚开始看的会很困惑，先看毛神的那篇总结心里会比较有数。

以下开始为正文，从原文第二章部分开始，中间其实说的挺啰嗦的，有基础的朋友其实可以直接跳到后面看总结。

表面辐射率的测量

辐射率是指从某个立体角到达的能量密度（ energy density）。当多个表面投影到一个相同的像素上时，这个像素上所测量到的总的辐射率

就是每个表面在像素上的投影面积的加权辐射率

的总和。

在计算机图形学中，BRDF建模了观察方向的辐射率，也就是说，抵达这个像素的平均能量。在观察方向每个表面的投影面积相当于一个与观察方向相关的权重因子，投影面积的总和

是一个重要的归一化系数（normalization coefficient）。除以这个总和以保证能量密度不变。

在接下来的章节里我们会看到，按照微表面理论，微表面同样也是这样被它们的投影面积加权的，而阴影遮挡函数（或者说几何衰减因子）是能量守恒所需的归一化系数。

微表面投影

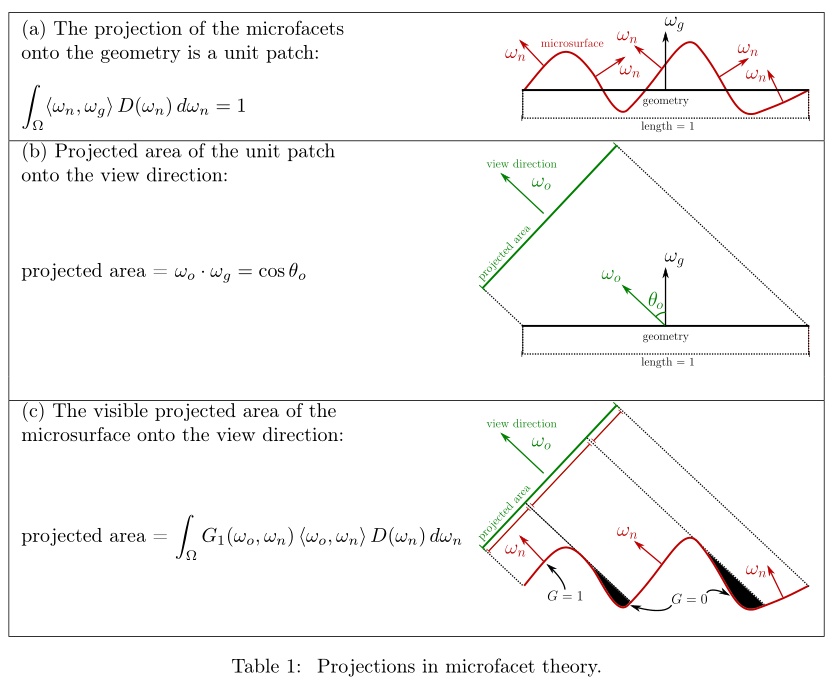
表格一展示了在微表面理论中不同类型的投影。

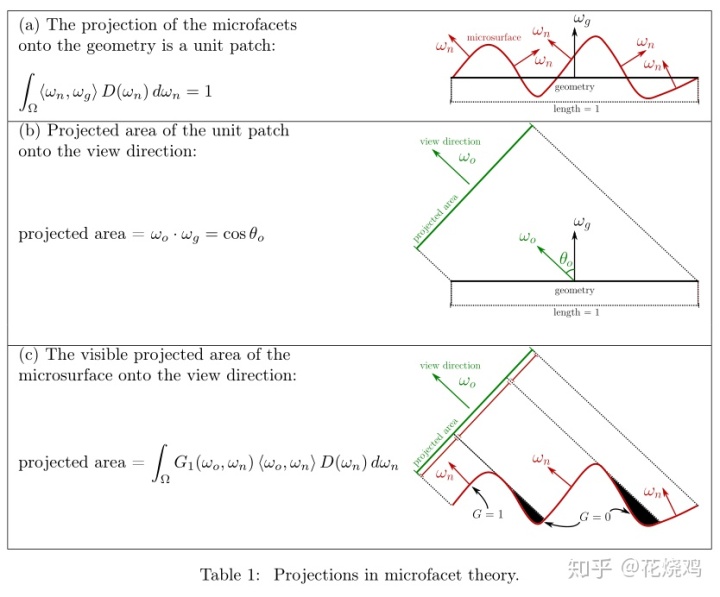
(a)投影到几何体上

微表面投影到几何体上的面积就是支持这些微表面的单位片段（ unit patch）的面积，通常来说都是1.因此，即便法线分布D不一定是球面归一化的（

），它们投影在几何体上面积也是归一化的。

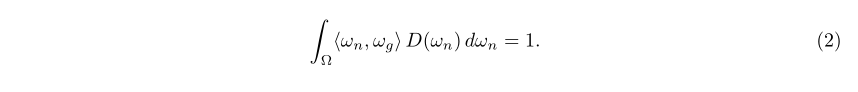
(b)单位片段的投影面积

由众多微表面所定义的那个单位片段是一个单位平面元素（unit planar element），它在观察方向的投影面积就是观察角度

的余弦值。

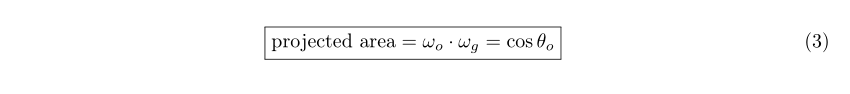
(c)微表面可见的投影面积

单位片段在观察角度的投影面积就是微表面可见的投影面积。它是每个微表面可见投影面积的总和。法线为

微表面的投影面积是与法线为

的微表面数量（由法线分布函数

给出）和几何投影项

成正比的。需要注意的是这个我们使用的是约束点乘（clamped dot product，译注：让结果不为负）因为背面剔除（ backface-culled ）的微表面不可见。同时，被其他微表面遮挡的微表面也对投影面积没有贡献，因此要从总和中移除。这是通过乘以一个范围在[0,1]之间的遮挡函数（ masking function）

并且给出在观察方向

可见的法线为

的微表面的比率完成的。被遮挡的法线为

的微表面因此就被丢弃掉了，最终微表面投影到观察方向上的面积就是：

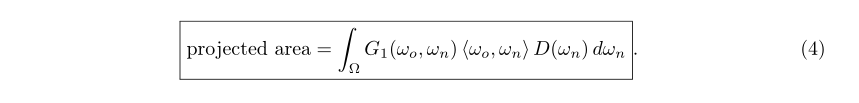
遮挡函数

在这一章中我们使用和投影面积有关的等式来介绍一个遮挡函数该有的约束。结合常见的——遮挡和法线分布是不相关的——这个假设，这个约束可以推导出Ashikhmin等人提出的准确遮挡函数

的积分形式。

遮挡函数的约束 表格1强调了微表面理论中的基本属性：等式（4）中的可见微表面的投影面积正是等式（3）中几何片段的投影面积。这种等价为遮挡函数加上了一个约束，可以用以下等式表示：

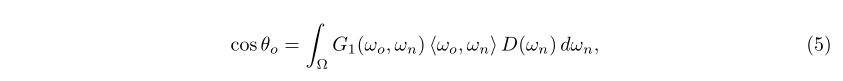
然而，这对于完全定义一个

是不够的。因为对于一个固定的观察角度

来说，它的遮挡函数是一个连续的2D函数（

是根据每个法线方向定义的）。

法线/遮挡独立 一个经典的微表面理论假说就是：遮挡函数

和没有被背面剔除的法线

是相互独立的。这个假说背后的直觉就是法线

是微表面的一个局部属性，然而可能的遮挡发生在表面的地方，因此它是微表面的一个非局部的属性。这就是为什么假设它们两个没有关系是合理的。同样，必须注意的是这种独立性仅在没有被背面剔除的法线上成立。实际上，被背面剔除的法线通常都被它们自己遮蔽了。在这种情况下，遮挡的概率就是一种局部的属性。这种法线和遮挡之间的独立性使我们能分离积分中的法线部分：

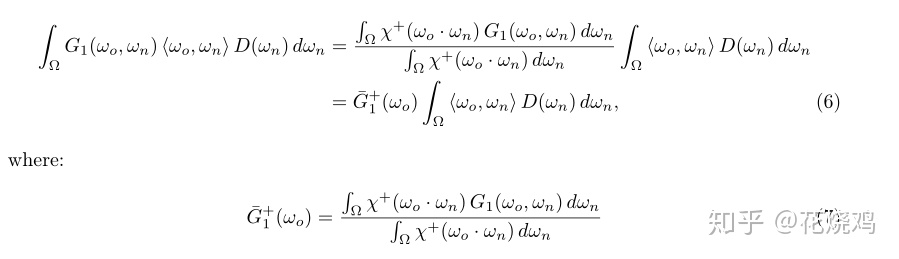
没有第二项的话就是观察方向的非剔除法线的平均遮挡函数。

遮挡函数的积分形式 通过结合等式（5）和（6），我们可以得到

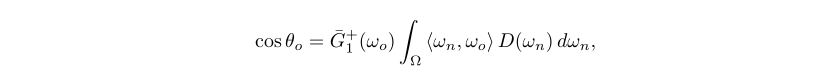
所以对于观察方向的可见法线的遮挡函数可以表示成：

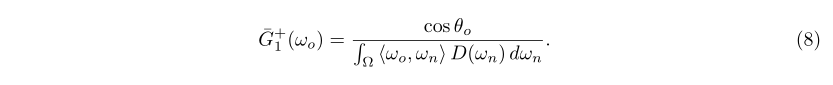
至此我们推导出了非背面剔除法线的平均遮挡函数，并且我们知道背面剔除法线的

，我们可以通过乘上一个海维赛德函数来定义所有法线的遮蔽项。

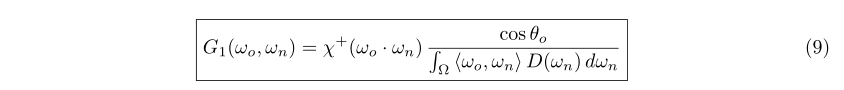
这是Ashikhmin等人在法线、掩蔽相互独立的假设下剔除的准确遮蔽函数的积分形式。它们使用积分表示来预计算遮蔽函数，并且将它存储在一个查阅表中，用来渲染。

Smith遮挡函数 通过将积分与从法向转换成斜率空间（原文附录里提供了具体的推导过程），我们可以将等式（9）重新改写成：

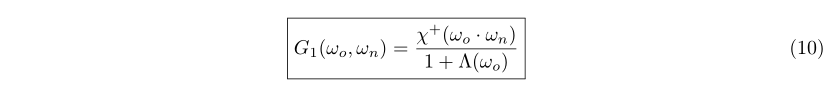
其中

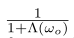
是Smith遮挡函数的一个一般形式，在第三章我们可以看到对于很多随机的表面这个函数也有闭合解。请注意，到目前为止我们所做的唯一假设就是遮挡和法线分布不相关，而且这个假说是微表面BRDF理论中早就提出来的。因此，在这种一般性的假设之下，Smith遮挡函数是准确的。

译注：从附录中可知：

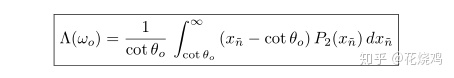
其中

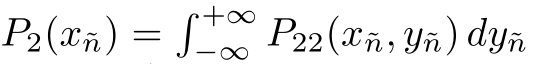
是一个一维的视角方向的斜率分布（和x轴平行）。

是斜率分布。它和法线分布的关系是：

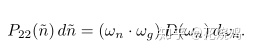
Smith的平均遮挡函数 Smith推导出遮挡函数在不同数量上面上的平均值，比如说高度或者法线不同的面。等式（10）给出的遮挡函数

是一个在各个微表面高度上平均的形式，并且是一定会被用在BRDF中的。事实上，因为高度这个属性和会影响BRDF的属性是不相关的，所以我们可以直接取平均。然而，法线不是这样子的：被背面剔除的法线没有被考虑。在BRDF模型中，只有外部观察者能看到的东西才重要，因为只有观察者能测量的辐射率才起作用。如果有什么东西存在在表面上却不能被看到，它不会被纳入BRDF模型中。在BRDF问题中我们实际上很关心一个问题：“多少没有被背面剔除的法线被遮挡了？”

既然法线平均在BRDF模型中没有用处，那所以为什么Smith推导了一个这种形式的遮挡函数呢？他实际上想回答的问题是：“多少法线被遮挡了？”第二个问题的答案对于研究表面固有属性是很重要，但是对BRDF不是。

所以这使我们得出一个重要的观察结论：既然我们只积分可见的辐射率，那我们应该保证这个定义域内的归一化而不是整个微表面。这就是第4节的内容。

总结：

一个经常被问及的问题就是“在这么多遮挡函数（或者几何衰减因子）里，我该用哪个？他们都是在物理上正确的么。”

典型的回答就是：“最好选择Smith遮挡函数，因为它取决于法线分布。”

在这一节中，通过以下想法的建立，我们证明了这个回答是正确的但是所援引的理由是错的：

• 在任何投影角度下，可见微表面的投影面积等价于宏观几何的投影面积。
• 遮挡函数被这种等价所约束
• 通常的微表面BRDF函数假设可见法线的朝向和遮挡的概率是无关的。
• 在这种假设之下，可以完全确定一个遮挡函数。它的准确形式可以被推导出来并且就是Smith方程的一般形式。

重要的点在于我们选择Smith遮挡函数并不是因为它是一个将法线分布参数化而做出上的物理上的近似。真正的选择Smith方程的原因是因为它的公式是在BRDF模型假设（法线分布和遮挡不相关）下的一个准确形式。事实上它在物理上看似合理并且根据法线分布参数化并不是我们选择它的直接理由，而是我们选择了它以后一些恰好符合了预期的副作用。

然而，如果我们将分析函数和实测数据进行比较，我们会发现这个预测模型并不准确。确实，Smith把他这个方程和真实世界的测量比较了一下然后就发现这不是一个好的近似，仅仅就是一个近似而已。但是近似并不存在于他的推导中，在他模型的框架里他的方程式准确的。相反，近似存在与统计模型对真实世界表面的描述中（比如高斯统计），和法线遮挡独立性的假设中。

译注：毛神的白皮书中有一段这样的话：
“ 几何函数的解析形式的确认依赖于法线分布函数。在微平面理论中，通过可见微平面的投影面积之和等于宏观表面的投影面积的恒等式，选定法线分布函数，并选定几何函数的模型，就可以唯一确认几何函数的准确形式。在选定几何函数的模型后（一般为Smith），几何函数的解析形式的确认则由对应的法线分布函数决定。”
应该可以说是对这一章的一个总结吧。之前不太理解什么叫“准确形式”什么叫“解析形式”，在读完这一章大概就有数了。准确形式是指在推导这个公式的时候没有用到近似，因此得出的结果是“准确”的，解析形式就是一般意义上的“给出解的具体函数 形式，从解的表达式中就可以算出任何对应值”。

Reference：

Heitz E. Understanding the masking-shadowing function in microfacet-based BRDFs[J]. 2014.