目录
第十三节课 : Ray tracing(光线追踪 1)
为什么要使用光线追踪?
为了使用光线追踪, 提出三个关于光线的假设
光线追踪的步骤
光线追踪 -- 产生眼睛光线
第一条光线的描述
第二条光线的描述
(Whitted-Style)递归的光线追踪
① 镜面反射(产生反射光)
② 镜面折射(产生折射光)
③ 每个交点都与光源连线, 判断是否为光源可见
④ 对每个交点进行阴影计算, 结果都要考虑进同一个像素的着色
⑤ 简单定义
射线表面交点
射线在球面上的交点
数学上, 交点p必须同时满足射线方程和球面方程
解出上述公式, 得到t的表达式
光线与隐式曲面的交点
t值有两个限制: 1.必须是实数 2.正数(光线是正方向的)
定论
光线与三角形曲面的交点
将光线在三角形的交点问题分为两个部分
Moller Trumbore 算法 (简称MT算法)
总结
简单光线追踪的执行问题
Bounding Volumes(包围盒)
盒子是3对平面(前后,上下和左右)的交集
在2D情况下轴对齐盒
在3D情况下的轴对齐盒
总结
第十三节课 : Ray tracing(光线追踪 1)
为什么要使用光线追踪?
光栅化不能很好地处理全局效应
-软阴影
-特别是当光线反弹不止一次时

光栅化速度快, 但是质量相对较低

光线追踪是准确的,符合物理. 但是非常慢
光栅化: 实时 , 光线追踪: 离线的
一核CPU需要10K小时,在生产中渲染一帧

为了使用光线追踪, 提出三个关于光线的假设 :
① 光以直线传播(尽管这是错误的)
② 如果光线交叉,不会相互碰撞(尽管这仍然是错误的)
③ 光线从光源传播到眼睛(但在光路可逆性作用下,物理学是不变的),因此可以假设眼睛发出感知光的线,经过各种反射最终到达光源.
光线追踪类似于 “人的眼睛发出感觉光线进入世界”
下图是以前错误的结论

光线追踪的步骤:
① 生成一个在摄像机面前的图, 这个图由很多像素组成, 从摄像机出发, 经过某个指定像素, 射向场景中的某个点.
② 从场景中某个点射向点光源一条射线, 通过是否有遮挡, 可以判断该点是否有阴影
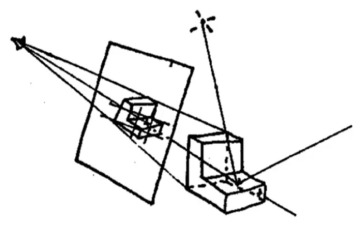
光线追踪 -- 产生眼睛光线
(假设为针孔摄像机, 没有体积)
第一条光线的描述如下:
① 眼睛光线从眼睛出发, 并且穿过像素
② 穿过像素后, 求眼睛光线与场景的最近交点.
③ 产生交点后, 就遮挡了这条眼睛光线后面可能会有的更多交点
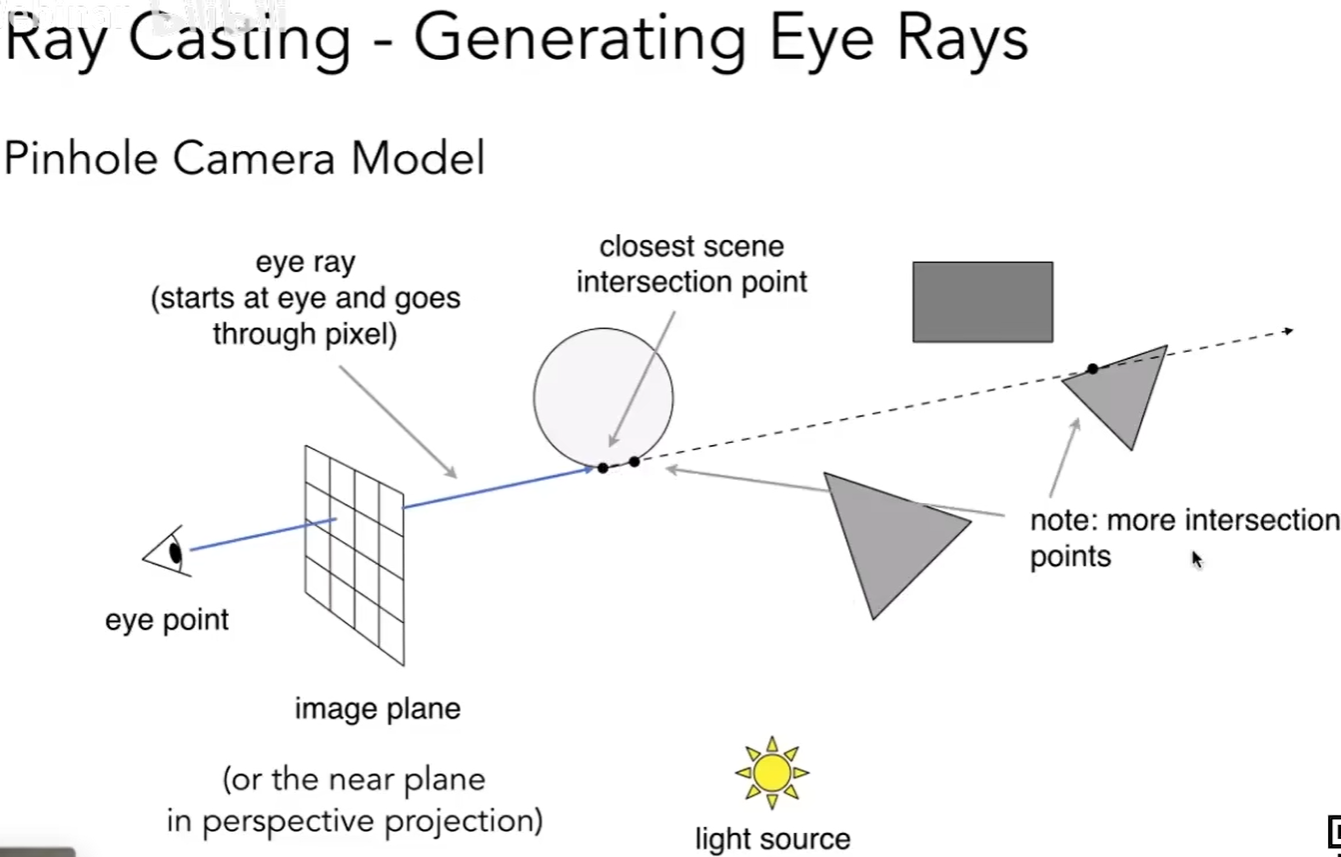
第二条光线描述如下:
① 连接交点与点光源, 检测是否有物体阻挡, 也就是检测交点是否为点光源所见.
② 根据该点的法线, 入射角度和出射角度执行阴影计算, 结果写入先前所经过像素的颜色.

递归的(Whitted-Style)光线追踪
Whitted-style假设反射都是完美反射
下面该球为玻璃球, 可折射可反射.
光线路径步骤如下:
① 镜面反射(产生反射光)

② 镜面折射(产生折射光)
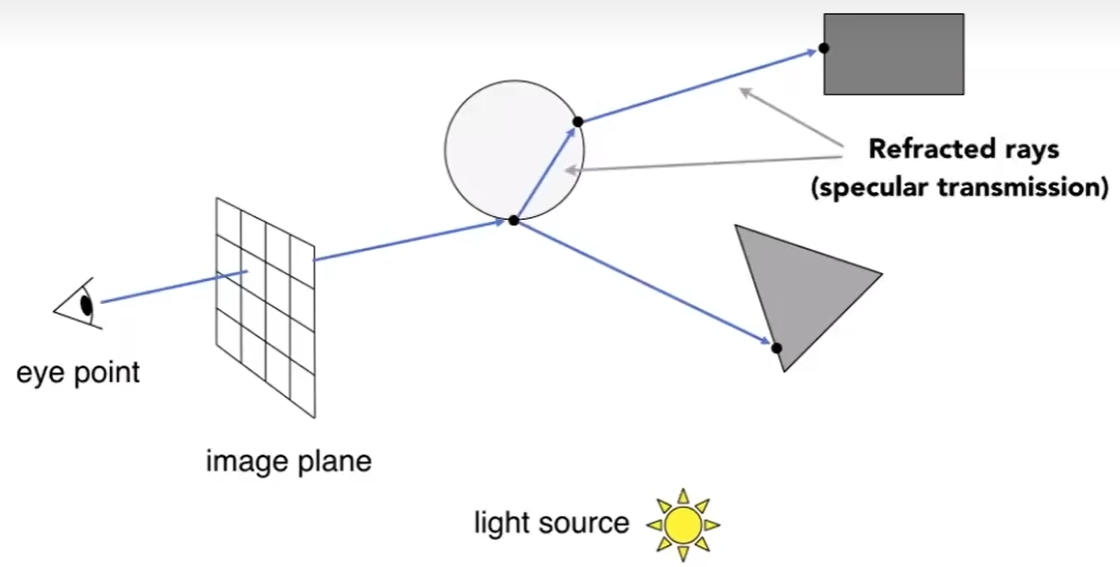
③ 每个交点都与光源连线, 判断是否为光源可见.

④ 对每个交点进行阴影计算, 结果都要考虑进同一个像素的着色.
考虑能量的损耗, 入射和出射角度, 光源可见性, 材质等等.

⑤ 简单定义:
Primary ray : 眼睛光线最开始接触场景的射线
Secondary rays : 经过反射,折射等等变化后的射线
Shadow ray : 交点与点光源连线的射线, 判断光源可见性

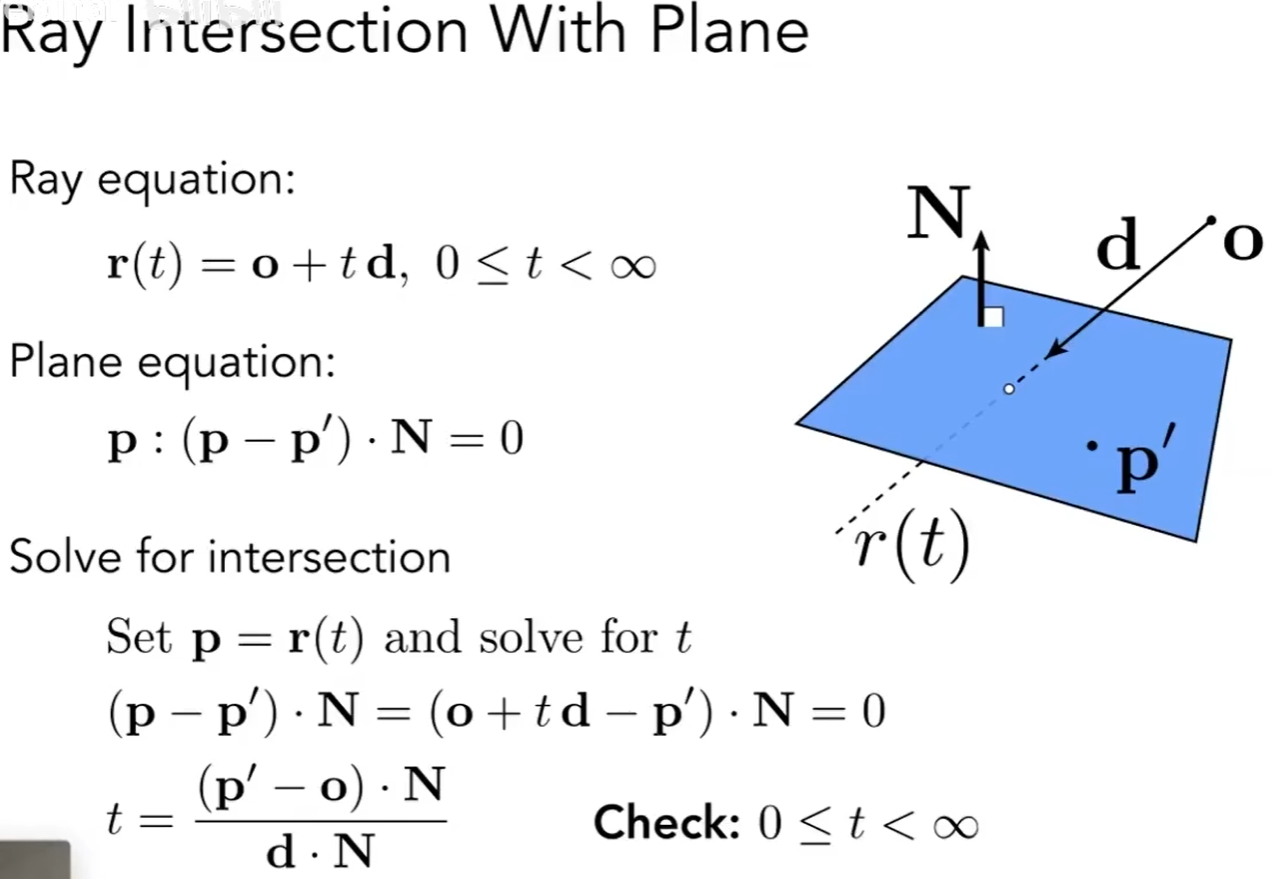
射线表面交点Ray-Surface Intersection
定义一个起点, 和一个方向, 代表射线
o :光线的起点 d :光线方向(单位向量) 由于光是射线, 所以t是时间 (0<= t <=无穷大)

射线在球面上的交点Ray Intersection With Sphere
数学上, 交点p必须同时满足射线方程和球面方程
最后得出下图中最下面的公式

解出上述公式, 得到t的表达式
根据(b的平方 - 4ac)>0得到两个交点, 则选择最近的一个; 或是=0, 则得到唯一交点; <0无意义.

光线与隐式曲面的交点Ray Intersection With Implicit Surface
假设光线与隐式曲面会有交点p的情况下, 所以p=o+td, 将光线方程代入隐式曲面方程得出新方程, 进而算出t.
t值有两个限制: 1.必须是实数 2.正数(光线是正方向的)

定论:
给定一个点在封闭的2D图形或者3D几何, 发出一条射线判断它的交点是奇数还是偶数. 若为奇数则在里面, 为偶数则在外面
光线与三角形曲面的交点
只需要求光线与每个三角形面的交点, 然后算出最小的t值. 则得出离点光源最近的点.
但是非常慢, 后面会讲加快方法.
给定一个三角形面, 一个光线, 要么产生一个交点, 要么没有交点.

将光线在三角形的交点问题分为两个部分 :
1.计算出光线在平面的交点
2. 判断该交点是否在三角形内

1.1 定义平面的方程式:
给定一个点p’和法线N, p是假设的随便一个点
(p-p’)点乘N若为0, 则p在平面内.否则不在.
p:(p-p’)点乘N=0 , 符合这个表达式的集合p就是拥有法线N的平面

1.2 计算平面上的交点, 根据光线方程和平面方程, 解出t值.
2.判断该点是否在三角形内, 这里不再解释, 因为在光栅化章节已经做过.
是否能直接判断交点是否在三角形内?
答案是可以.
引入一个算法: Moller Trumbore 算法 (简称MT算法)
看下图
等式左边o+tD是光线方程.
等式右边(1-b1-b2)p0+b1p1+b2p2是三角形的重心坐标方程
最后根据MT算法, 得出t,b1,b2的值.
数值限制: 0<= t <=无穷大 / b1>0 / b2>0

以上为简单的光线-场景的相交, 总结为:
1.详尽地测试与每个对象(三角形,像素)的光线相交
2.找到距离最短的交点(最小t)
简单光线追踪的执行问题:
相关像素数量*相关三角形面(*折射次数) : 太多的计算量, 导致运行速度太慢了
下面的场景三角形数太多了, 使用简单光线追踪根本不行.为了加快速度, 引入了Bounding Volumes(包围盒)

Bounding Volumes(包围盒)
计算交点的快速方法:用一个简单的盒完全包住该复杂的对象中
如果它没有击中包围盒,它就不会击中对象
所以首先测试包围盒,然后测试对象是否命中

盒子是3对平面(前后,上下和左右)的交集
我们经常使用这个Axis-Aligned Bounding Box(AABB)(轴对齐包围盒)
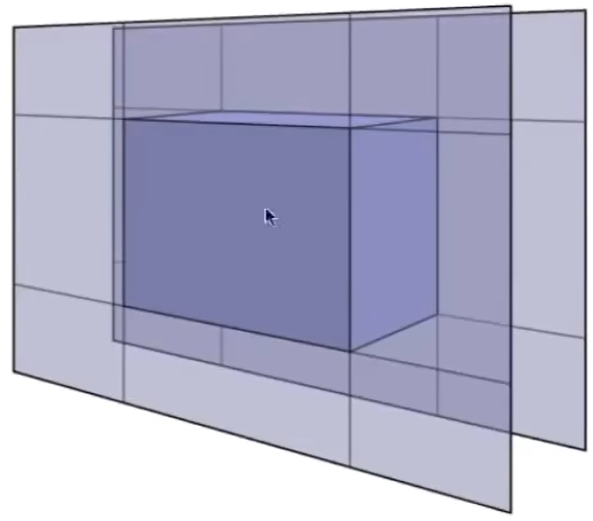

在2D情况下轴对齐盒;3d也是一样的,不过是多了一个变量
1.计算光线与平面的交集,共两个平面(x0~x1 / y0~y1), 并取它们各自tmin/tmax间的交集
2.光线与x0~x1的交集(左图), 光线与y0~y1的交集(中图)
3.因为这个Box是由两个平面的交集而成的, 所以求出上述两个交集的交集后, 就得到实际光线进入包围盒的进入和离开时间(右图)

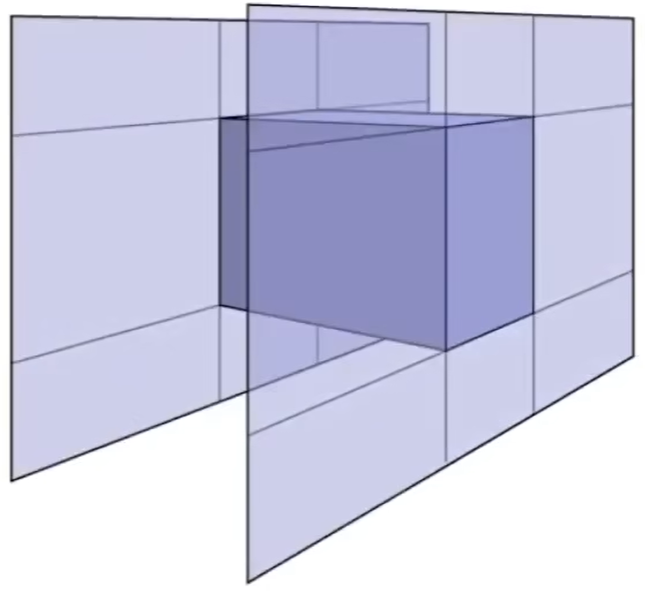
在3D情况下的轴对齐盒
轴对齐盒 = 3对无限大的对齐平面
关键思想:
① 只有当光线进入所有的平面时,光线才会进入盒子
② 只要光线离开任何一对平面,光线就会离开盒子
- 对于每一对平面, 计算tmin和tmax
- 对于3D轴对齐盒来说(一共有三对平面,所以有三个tmin和tmax)
t_enter(光线进入时间) = max {tmin}, 因为关键思想1
t_exit(光线离开时间) = min {tmax}, 因为关键思想2
- 如果t_enter < t_exit, 就知道这个光线在盒子里呆了一会(有交点).
因为光线不是一个直线, 而是一条射线, 所以它的 t_enter 和 t_exit 可能为任何值, 显然上述方法并未考虑t_enter和t_exit为负值的情况.
在这里, 应该检查tmin/tmax的值.
① 当t_exit < 0, 包围盒在光线起点背后, 不会有交点.
② 当t_exit >=0 且 t_enter < 0, 这个时候光线的起点就在包围盒里, 所以不管它的方向如何, 都必然与包围盒有交点.
总结:
当且仅当 t_enter < t_exit && t_exit >= 0, 光线与AABB轴对齐包围盒有交点
一般情况下, 计算时间t的公式

以下情况的细节 : 节省时间 t 计算量
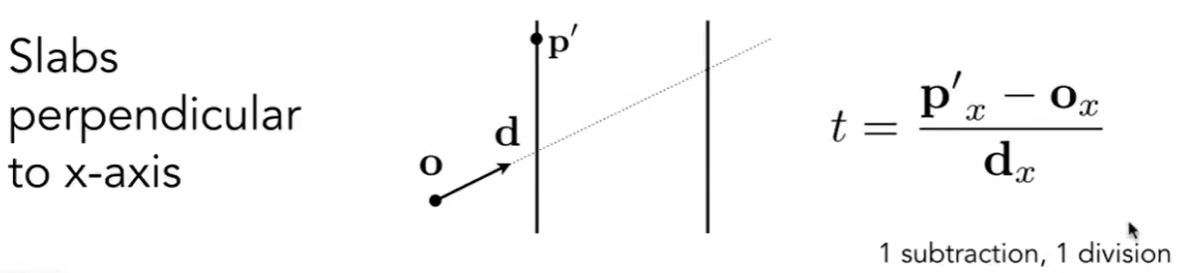
当某个对齐平面垂直于某条x,y,z轴时, 则
t= P’x - Ox/dx
t= P’y - Oy/dy
t= P’z - Oz/dz
例如下面例子, t= P’x - Ox/dx 可以理解为:
在P’x-Ox的路程下, 以dx的速度到达的tmin或tmax时间.
最后
以上就是疯狂牛排最近收集整理的关于Games101-课程13笔记第十三节课 : Ray tracing(光线追踪 1)的全部内容,更多相关Games101-课程13笔记第十三节课内容请搜索靠谱客的其他文章。








发表评论 取消回复