Game101课程笔记_lecture02_线性代数(图形学)
- 1 图形学需要的基础
- 2 线性代数
- 1 向量概念
- 2 vector normalization向量规范化
- 3 向量加法
- 4 向量的点乘 Dot product
- 5 向量的叉乘 Cross product
- 6 正交坐标系
- 2 矩阵
- 1 概念
- 2 矩阵的乘积
- 3 矩阵相乘的特性
- 4 矩阵向量相乘
- 5 矩阵的转置
- 6 单位矩阵
- 7 向量的乘积的矩阵形式
- 3 视频
1 图形学需要的基础
- 数学:线性代数,微积分,统计学
- 物理:光学,力学
- 其他:信号处理,数值分析
- 一点美学
2 线性代数
1 向量概念
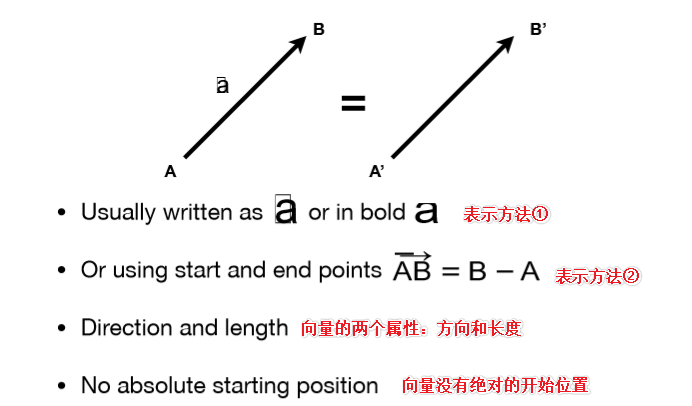
2 vector normalization向量规范化

3 向量加法
向量的加法可以从两个角度去理解:
- 从几何的角度去理解:平行四边形法则和三角形法则
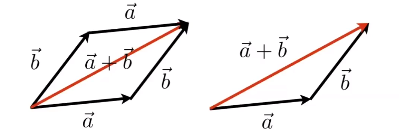
- 坐标系中相应的坐标相加
将向量表示成坐标的形式是非常有助于计算向量的长度的;
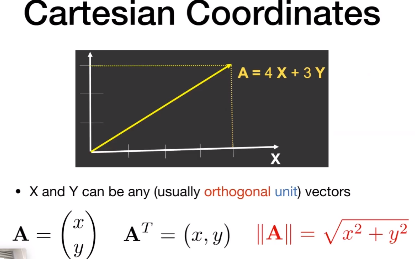
4 向量的点乘 Dot product
两个向量的点乘是一个数;
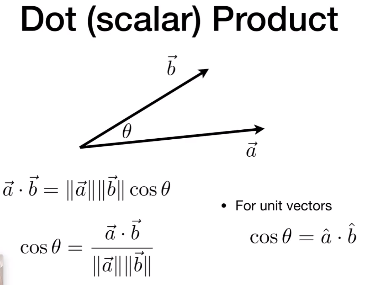
可以快速计算两个向量之间的夹角;
向量点乘的基本属性:
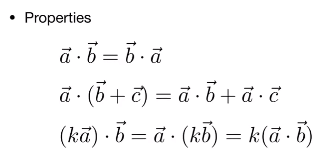
在直角坐标系中的计算公式如下:

向量点乘在图形学中的用法:
- 快速找到两个向量之间的夹角;比如在
- 一个向量投影到另外一个向量上什么样子的
- 可以计算两个向量方向接近程度:根据点乘的结果来判断是接近和远离;比如在高光渲染的时候就要用这个知识
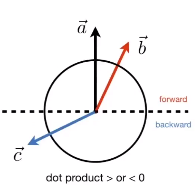
- 向量点乘还可以给出一个前与后的信息:如果落在了上半圆就是接近,如果落在了下半圆就是远离。根据点乘的符号来判断,如果是正的,结果等于1就是相同,如果是-1是相向;

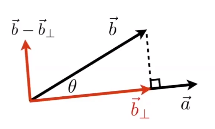
投影-可以将一个向量分解成两个向量,一个向量平行于第一个向量,另外一个向量垂直于第一个向量;
5 向量的叉乘 Cross product
向量叉乘的结果是一个向量!方向用右手螺旋定则确定(或者左手)
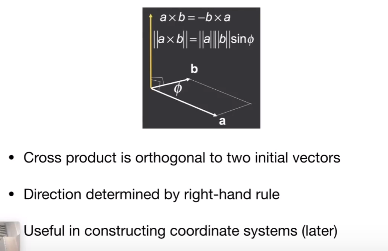
右手螺旋定则:
OpenGL中使用的是左手坐标系!


叉乘在图形学中的意义:
- 判断左和右
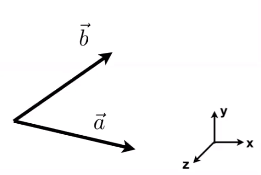
如下图:判断b在a的左边还是右边
用a叉乘b,得到的结果是正的,说明b在a的左侧
用b叉乘a,得到的结果是负的,说明b在a的右侧
- 判断里和外
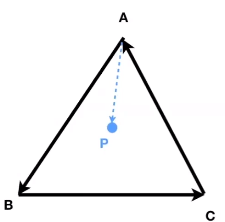
判断P在三角形ABC的内部?
ABXAP,结果是正的,说明P在AB的左侧
BCXBP,结果是正的,说明P在AB的左侧
CAXPC,结果是正的,说明P在CA的左侧
所以P在三角形ABC的内部,
绕的顺序是AB-BC-CA,绕向逆时针和顺时针,也就是三个叉乘结果要嘛都是正的,要嘛都是负的
这个是三角形光栅化的基础,要知道三角形覆盖了哪些像素,判断像素是否在三角形内部;
6 正交坐标系

2 矩阵
1 概念
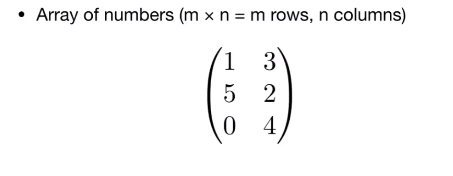
2 矩阵的乘积

有个简单的记忆方法:
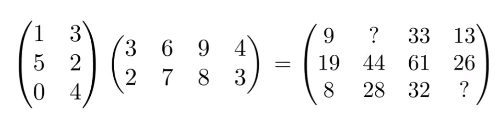
26是结果的二行四列:
找第一个矩阵的第二行(5,2),第二个矩阵的第四列(4,3),把两个向量求个点积就可以了。
再测试一个,61是二行三列
第三行(5,2)和第三列(9,8)求点击就是61;
也就是需要算第几行第几列的数值,直接子在输入矩阵中找第几行第几列就可以了!
3 矩阵相乘的特性
没有交换律

4 矩阵向量相乘
始终任务矩阵在左边,向量在右边
将向量看成是mx1的矩阵
点的变换就是基于这个知识点
5 矩阵的转置

6 单位矩阵
矩阵的逆
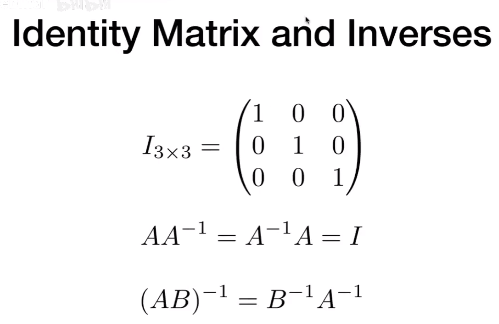
7 向量的乘积的矩阵形式
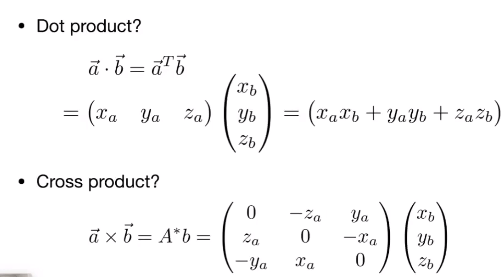
这个性质在推旋转的时候很有用的
3 视频
https://www.bilibili.com/video/av90798049?p=2
最后
以上就是标致鱼最近收集整理的关于Game101课程笔记_lecture02_线性代数(图形学)1 图形学需要的基础2 线性代数2 矩阵3 视频的全部内容,更多相关Game101课程笔记_lecture02_线性代数(图形学)1内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复