本文为强化学习笔记,主要参考以下内容:
- Reinforcement Learning: An Introduction
- 代码全部来自 GitHub
- 习题答案参考 Github
目录
- TD Prediction
- Advantages of TD Prediction Methods
- Optimality of TD(0)
- Sarsa: On-policy TD Control
- Q-learning: Off-policy TD Control
- Expected Sarsa
- Maximization Bias and Double Learning
- Games, Afterstates, and Other Special Cases
TD learning is a combination of Monte Carlo ideas and dynamic programming (DP) ideas.
- Like Monte Carlo methods, TD methods can learn directly from raw experience without a model of the environment’s dynamics.
- Like DP, TD methods update estimates based in part on other learned estimates, without waiting for a final outcome (they bootstrap).
- For the control problem (finding an optimal policy), DP, TD, and Monte Carlo methods all use some variation of generalized policy iteration (GPI). The differences in the methods are primarily differences in their approaches to the prediction problem.
The special cases of TD methods introduced in the present chapter should rightly be called o n e one one- s t e p step step, t a b u l a r tabular tabular, m o d e l model model- f r e e free free TD methods.
- In the next two chapters we extend them to n n n-step forms (a link to Monte Carlo methods) and forms that include a model of the environment (a link to planning and dynamic programming).
- Then, in the second part of the book we extend them to various forms of f u n c t i o n function function a p p r o x i m a t i o n approximation approximation rather than tables (a link to deep learning and artificial neural networks).
TD Prediction
TD VS Monte Carlo methods
- Both TD and Monte Carlo methods use experience to solve the prediction problem.
- Roughly speaking, Monte Carlo methods wait until the return following the visit is known, then use that return as a target for
V
(
S
t
)
V (S_t)
V(St). A simple every-visit Monte Carlo method suitable for nonstationary environments is
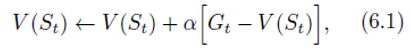 where
G
t
G_t
Gt is the actual return following time
t
t
t, and
α
alpha
α is a constant step-size parameter. Let us call this method
c
o
n
s
t
a
n
t
constant
constant-
α
alpha
α MC.
where
G
t
G_t
Gt is the actual return following time
t
t
t, and
α
alpha
α is a constant step-size parameter. Let us call this method
c
o
n
s
t
a
n
t
constant
constant-
α
alpha
α MC.
( α = 1 k alpha=frac{1}{k} α=k1 if V ( S t ) ← a v e r a g e ( R e t u r n s ( S t ) ) V(S_t)leftarrow average(Returns(S_t)) V(St)←average(Returns(St))) - TD methods need to wait only until the next time step. At time
t
+
1
t + 1
t+1 they immediately form a target and make a useful update using the observed reward
R
t
+
1
R_{t+1}
Rt+1 and the estimate
V
(
S
t
+
1
)
V (S_{t+1})
V(St+1). The simplest TD method makes the update
 immediately on transition to
S
t
+
1
S_{t+1}
St+1 and receiving
R
t
+
1
R_{t+1}
Rt+1. In effect, the target for the TD update is
R
t
+
1
+
γ
V
(
S
t
+
1
)
R_{t+1}+gamma V (S_{t+1})
Rt+1+γV(St+1). (a
b
o
o
t
s
t
r
a
p
p
i
n
g
bootstrapping
bootstrapping method)
immediately on transition to
S
t
+
1
S_{t+1}
St+1 and receiving
R
t
+
1
R_{t+1}
Rt+1. In effect, the target for the TD update is
R
t
+
1
+
γ
V
(
S
t
+
1
)
R_{t+1}+gamma V (S_{t+1})
Rt+1+γV(St+1). (a
b
o
o
t
s
t
r
a
p
p
i
n
g
bootstrapping
bootstrapping method)
- Roughly speaking, Monte Carlo methods wait until the return following the visit is known, then use that return as a target for
V
(
S
t
)
V (S_t)
V(St). A simple every-visit Monte Carlo method suitable for nonstationary environments is
TD VS Monte Carlo VS DP methods
- We know that

- Roughly speaking, Monte Carlo methods use an estimate of (6.3) as a target. The Monte Carlo target is an estimate because the expected value in (6.3) is not known; a sample return is used in place of the real expected return
- DP methods use an estimate of (6.4) as a target. The DP target is an estimate because v π ( S t + 1 ) v_pi(S_{t+1}) vπ(St+1) is not known and the current estimate, V ( S t + 1 ) V (S_{t+1}) V(St+1), is used instead.
- The TD target is an estimate for both reasons:
- it samples the expected values in (6.4) and it uses the current estimate V V V instead of the true v π v_pi vπ.
- Thus, TD methods combine the sampling of Monte Carlo with the bootstrapping of DP.
s a m p l e sample sample u p d a t e s updates updates VS e x p e c t e d expected expected u p d a t e s updates updates
- S a m p l e Sample Sample updates (TD, MC) differ from the e x p e c t e d expected expected updates (DP) methods in that they are based on a single sample successor rather than on a complete distribution of all possible successors.
- This TD method is called T D ( 0 ) TD(0) TD(0), or one-step TD, because it is a special case of the T D ( λ ) TD(lambda) TD(λ) and n n n-step TD methods developed in Chapter 12 and Chapter 7.

T D TD TD e r r o r error error

- Notice that δ t delta_t δt is the error in V ( S t ) V (S_t) V(St), available at time t + 1 t + 1 t+1.
- Also note that if the array
V
V
V does not change during the episode (as it does not in Monte Carlo methods), then the Monte Carlo error can be written as a sum of TD errors:
 This identity is not exact if
V
V
V is updated during the episode (as it is in TD(0)), but if the step size is small then it may still hold approximately.
This identity is not exact if
V
V
V is updated during the episode (as it is in TD(0)), but if the step size is small then it may still hold approximately.
- Generalizations of this identity play an important role in the theory and algorithms of temporal-difference learning.
Exercise 6.1
If V V V changes during the episode, then (6.6) only holds approximately; what would the difference be between the two sides? Let V t V_t Vt denote the array of state values used at time t t t in the TD error (6.5) and in the TD update (6.2). Redo the derivation above to determine the additional amount that must be added to the sum of TD errors in order to equal the Monte Carlo error.
ANSWER
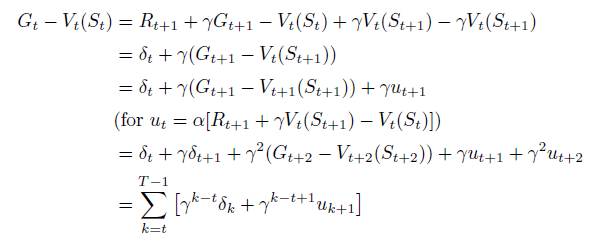
T D TD TD m e t h o d s methods methods VS M C MC MC m e t h o d s methods methods
Example 6.1: Driving Home
- Each day as you drive home from work, you try to predict how long it will take to get home. The sequence of states, times, and predictions is as follows:

- The rewards in this example are the elapsed times on each leg of the journey. We are not discounting (
γ
=
1
gamma = 1
γ=1), and thus the return for each state is the actual time to go from that state. The value of each state is the expected time to go. The second column of numbers gives the current estimated value for each state encountered.

Here, α = 1 alpha=1 α=1 in the T D TD TD method
Exercise 6.2
- This is an exercise to help develop your intuition about why TD methods are often more efficient than Monte Carlo methods. Consider the driving home example and how it is addressed by TD and Monte Carlo methods. Can you imagine a scenario in which a TD update would be better on average than a Monte Carlo update?
- Give an example scenario—a description of past experience and a current state—in which you would expect the TD update to be better. Here’s a hint: Suppose you have lots of experience driving home from work. Then you move to a new building and a new parking lot (but you still enter the highway at the same place). Now you are starting to learn predictions for the new building. Can you see why TD updates are likely to be much better, at least initially, in this case? Might the same sort of thing happen in the original scenario?
ANSWER
- The example scenario is very effcient for TD because states of the highway part are not changed, and we can still have a solid belief of its state value. Utilizing TD will accelerate our adjustment of our new states. Each updated state will then accelerate the one prior to it.
- Monte Carlo, on the other hand, has to go to the end and bring average improvement of all states, especially those high way parts, which do not need too much adjustment at all but will still be fluctuated by the Monte Carlo method.
- Another situation where TD is much more effcient is when we are very diffcult to make to the terminal state.
Advantages of TD Prediction Methods
- TD methods update their estimates based in part on other estimates. They learn a guess from a guess—they b o o t s t r a p bootstrap bootstrap. Is this a good thing to do?
- What advantages do TD methods have over DP methods?
The most obvious advantage of TD methods over Monte Carlo methods is that they are naturally implemented in an online, fully incremental (完全递增的) fashion.
- With Monte Carlo methods one must wait until the end of an episode, whereas with TD methods one need wait only one time step.
Surprisingly often this turns out to be a critical consideration.
- Some applications have very long episodes, so that delaying all learning until the end of the episode is too slow.
- Other applications are continuing tasks and have no episodes at all.
- Finally, some Monte Carlo methods must ignore or discount episodes on which experimental actions are taken, which can greatly slow learning.
- TD methods are much less susceptible to these problems because they learn from each transition regardless of what subsequent actions are taken.
But are TD methods sound?
- Happily, the answer is yes.
- For any fixed policy π pi π, TD(0) has been proved to converge to v π v_pi vπ, in the mean for a constant step-size parameter if it is sufficiently small, and with probability 1 if the step-size parameter decreases according to the usual stochastic approximation conditions (2.7).
- Most convergence proofs apply only to the table-based case of the algorithm presented above (6.2), but some also apply to the case of general linear function approximation. These results are discussed in a more general setting in Section 9.4.
If both TD and Monte Carlo methods converge asymptotically to the correct predictions, then a natural next question is “Which gets there first?”
- At the current time this is an open question in the sense that no one has been able to prove mathematically that one method converges faster than the other.
- In practice, however, TD methods have usually been found to converge faster than constant- α alpha α MC methods on stochastic tasks.
Tips:
- Sufficiently small α alpha α is the convergence requirement for both TD and Monte Carlo. Thus, one could say small α alpha α in TD and Monte Carlo is always better than large ones in the long run and is reaching lowest error it can reach in the limit.
- On the other hand, one could expect a changing α alpha α or changing weight for different states will be handy, and it will be covered in much later chapters.
Optimality of TD(0)
TD(0) 的最优性
b a t c h boldsymbol {batch} batch u p d a t i n g boldsymbol {updating} updating
- Suppose there is available only a finite amount of experience, say 10 episodes or 100 time steps. In this case, a common approach with incremental learning methods is to present the experience repeatedly until the method converges upon an answer.
- Given an approximate value function,
V
V
V , the increments specified by (6.2) are computed for every time step
t
t
t at which a nonterminal state is visited, but the value function is changed only once, by the sum of all the increments.
 Then all the available experience is processed again with the new value function to produce a new overall increment, and so on, until the value function converges. We call this
b
a
t
c
h
batch
batch
u
p
d
a
t
i
n
g
updating
updating because updates are made only after processing each complete batch of training data.
Then all the available experience is processed again with the new value function to produce a new overall increment, and so on, until the value function converges. We call this
b
a
t
c
h
batch
batch
u
p
d
a
t
i
n
g
updating
updating because updates are made only after processing each complete batch of training data.
- Given an approximate value function,
V
V
V , the increments specified by (6.2) are computed for every time step
t
t
t at which a nonterminal state is visited, but the value function is changed only once, by the sum of all the increments.
- Under batch updating, TD(0) converges deterministically to a single answer independent of the step-size parameter, α alpha α, as long as α alpha α is chosen to be sufficiently small.
- The constant-
α
alpha
α MC method also converges deterministically under the same conditions, but to a different answer.
- Understanding these two answers will help us understand the difference between the two methods. Before trying to understand the two answers in general, for all possible tasks, we first look at a few examples.
Example 6.3: Random walk under batch updating
- Understanding these two answers will help us understand the difference between the two methods. Before trying to understand the two answers in general, for all possible tasks, we first look at a few examples.
Example 6.4: You are the Predictor
- Place yourself now in the role of the predictor of returns for an unknown Markov reward process. Suppose you observe the following eight episodes:
 This means that the first episode started in state
A
A
A, transitioned to
B
B
B with a reward of 0, and then terminated from
B
B
B with a reward of 0. The other seven episodes were even shorter, starting from
B
B
B and terminating immediately.
This means that the first episode started in state
A
A
A, transitioned to
B
B
B with a reward of 0, and then terminated from
B
B
B with a reward of 0. The other seven episodes were even shorter, starting from
B
B
B and terminating immediately. - Given this batch of data, what would you say are the optimal predictions, the best values for the estimates
V
(
A
)
V (A)
V(A) and
V
(
B
)
V (B)
V(B)?
- Everyone would probably agree that the optimal value for V ( B ) V (B) V(B) is 3 4 frac{3}{4} 43, because six out of the eight times in state B B B the process terminated immediately with a return of 1, and the other two times in B B B the process terminated immediately with a return of 0.
- But what is the optimal value for the estimate
V
(
A
)
V (A)
V(A) given this data? Here there are two reasonable answers.
- One is to observe that 100% of the times the process was in state
A
A
A it traversed immediately to
B
B
B (with a reward of 0); and because we have already decided that
B
B
B has value
3
4
frac{3}{4}
43, therefore
A
A
A must have value
3
4
frac{3}{4}
43 as well. This is also the answer that batch TD(0) gives.

- The other reasonable answer is simply to observe that we have seen A A A once and the return that followed it was 0; we therefore estimate V ( A ) V (A) V(A) as 0. This is the answer that batch Monte Carlo methods give. Notice that it is also the answer that gives minimum squared error on the training data. In fact, it gives zero error on the data.
- But still we expect the first answer to be better. If the process is Markov, we expect that the first answer will produce lower error on future data, even though the Monte Carlo answer is better on the existing data.
- One is to observe that 100% of the times the process was in state
A
A
A it traversed immediately to
B
B
B (with a reward of 0); and because we have already decided that
B
B
B has value
3
4
frac{3}{4}
43, therefore
A
A
A must have value
3
4
frac{3}{4}
43 as well. This is also the answer that batch TD(0) gives.
Example 6.4 illustrates a general difference between the estimates found by batch TD(0) and batch Monte Carlo methods.
- Batch Monte Carlo methods always find the estimates that minimize mean-squared error on the training set.
- Batch TD(0) always finds the estimates that would be exactly correct for the maximum-likelihood model of the Markov process.
- In general, the m a x i m u m maximum maximum- l i k e l i h o o d likelihood likelihood e s t i m a t e estimate estimate of a parameter is the parameter value whose probability of generating the data is greatest.
- In this case, the maximum-likelihood estimate is the model of the Markov process formed in the obvious way from the observed episodes: the estimated transition probability from i i i to j j j is the fraction of observed transitions from i i i that went to j j j, and the associated expected reward is the average of the rewards observed on those transitions.
- Given this model, we can compute the estimate of the value function that would be exactly correct if the model were exactly correct. This is called the c e r t a i n t y certainty certainty- e q u i v a l e n c e equivalence equivalence e s t i m a t e estimate estimate (确定性等价估计) because it is equivalent to assuming that the estimate of the underlying process was known with certainty rather than being approximated. In general, batch TD(0) converges to the certainty-equivalence estimate.
This helps explain why TD methods converge more quickly than Monte Carlo methods.
- In batch form, TD(0) is faster than Monte Carlo methods because it computes the true certainty-equivalence estimate.
- The relationship to the certainty-equivalence estimate may also explain in part the speed advantage of nonbatch TD(0). Although the nonbatch methods do not achieve either the certainty-equivalence or the minimum squared-error estimates, they can be understood as moving roughly in these directions. Nonbatch TD(0) may be faster than constant- α alpha α MC because it is moving toward a better estimate, even though it is not getting all the way there.
- Finally, it is worth noting that although the certainty-equivalence estimate is in some sense an optimal solution, it is almost never feasible to compute it directly. If n = ∣ S ∣ n = |mathcal S| n=∣S∣ is the number of states, then just forming the maximum-likelihood estimate of the process may require on the order of n 2 n^2 n2 memory, and computing the corresponding value function requires on the order of n 3 n^3 n3 computational steps if done conventionally.
- In these terms it is indeed striking that TD methods can approximate the same solution using memory no more than order n n n and repeated computations over the training set. On tasks with large state spaces, TD methods may be the only feasible way of approximating the certainty-equivalence solution.
Sarsa: On-policy TD Control
- We turn now to the use of TD prediction methods for the control problem. As usual, we follow the pattern of generalized policy iteration (GPI), only this time using TD methods for the evaluation or prediction part.
- As with Monte Carlo methods, we face the need to trade off exploration and exploitation, and again approaches fall into two main classes: on-policy and off-policy. In this section we present an on-policy TD control method.
- The first step is to learn an action-value function rather than a state-value function. In particular, for an on-policy method we must estimate q π ( s , a ) q_pi(s, a) qπ(s,a). This can be done using essentially the same TD method described above for learning v π v_pi vπ.
- In the previous section we considered transitions from state to state and learned the values of states. Now we consider transitions from state–action pair to state–action pair, and learn the values of state–action pairs.
 Formally these cases are identical:
Formally these cases are identical:
- they are both Markov chains with a reward process. The theorems assuring the convergence of state values under TD(0) also apply to the corresponding algorithm for action values:
 This update is done after every transition from a nonterminal state
S
t
S_t
St. If
S
t
+
1
S_{t+1}
St+1 is terminal, then
Q
(
S
t
+
1
,
A
t
+
1
)
Q(S_{t+1},A_{t+1})
Q(St+1,At+1) is defined as zero.
This update is done after every transition from a nonterminal state
S
t
S_t
St. If
S
t
+
1
S_{t+1}
St+1 is terminal, then
Q
(
S
t
+
1
,
A
t
+
1
)
Q(S_{t+1},A_{t+1})
Q(St+1,At+1) is defined as zero.
- they are both Markov chains with a reward process. The theorems assuring the convergence of state values under TD(0) also apply to the corresponding algorithm for action values:
This rule uses every element of the quintuple (五元组) of events, ( S t , A t , R t + 1 , S t + 1 , A t + 1 ) (S_t,A_t,R_{t+1}, S_{t+1},A_{t+1}) (St,At,Rt+1,St+1,At+1), that make up a transition from one state–action pair to the next. This quintuple gives rise to the name S a r s a Sarsa Sarsa for the algorithm.

The convergence properties of the Sarsa algorithm depend on the nature of the policy’s dependence on Q Q Q.
- For example, one could use ε varepsilon ε-greedy or ε varepsilon ε-soft policies. Sarsa converges with probability 1 to an optimal policy and action-value function as long as all state–action pairs are visited an infinite number of times and the policy converges in the limit to the greedy policy (which can be arranged, for example, with ε varepsilon ε-greedy policies by setting ε = 1 t varepsilon= frac{1}{t} ε=t1).
Exercise 6.9: Windy Gridworld
Q-learning: Off-policy TD Control
- One of the early breakthroughs in reinforcement learning was the development of an off-policy TD control algorithm known as
Q
Q
Q-
l
e
a
r
n
i
n
g
learning
learning, defined by
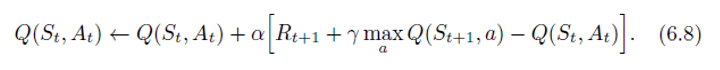
- In this case, the learned action-value function, Q Q Q, directly approximates q ∗ q_* q∗, the optimal action-value function, independent of the policy being followed.
- This dramatically simplifies the analysis of the algorithm and enabled early convergence proofs. The policy still has an effect in that it determines which state–action pairs are visited and updated. However, all that is required for correct convergence is that all pairs continue to be updated. As we observed in Chapter 5, this is a minimal requirement in the sense that any method guaranteed to find optimal behavior in the general case must require it. Under this assumption and a variant of the usual stochastic approximation conditions on the sequence of step-size parameters, Q Q Q has been shown to converge with probability 1 to q ∗ q_* q∗.

Exercise 6.11
Why is Q-learning considered an off-policy control method?
- The reason is that Q-learning tries to evaluate value function for greedy policy while following policy
π
pi
π. (behavior policy:
π
pi
π; target policy: greedy policy)
- In other words, it estimates the return (total discounted future reward) for state-action pairs assuming a greedy policy were followed despite the fact that it’s not following a greedy policy.
- The reason that SARSA is on-policy is that it updates its Q-values using the Q-value of the next state s s s and the current policy’s action a a a. It estimates the return for state-action pairs assuming the current policy continues to be followed.
Exercise 6.12
Suppose action selection is greedy. Is Q-learning then exactly the same algorithm as Sarsa? Will they make exactly the same action selections and weight updates?
- Sarsa:

- Q-learning:
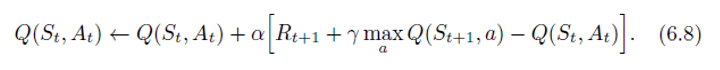
ANSWER
- They seem to be the same method in general. But it will be different in occasional situation.
- Consider S = S ′ S = S' S=S′ during some steps. During update, SARSA will use the previous greedy choice A ′ A' A′ made from S ′ S' S′, and advance to Q ( S ′ , A ′ ) Q(S',A') Q(S′,A′). But Q-learning will use the updated Q to re-choose greedy A ∗ A^* A∗. Because A ′ A' A′ may not be the same action as the new greedy choice A ∗ A^* A∗ that will maximize Q ( S ′ , A ∗ ) Q(S',A^*) Q(S′,A∗), these two methods are different.
Expected Sarsa
期望 Sarsa
- Consider the learning algorithm that is just like Q-learning except that instead of the maximum over next state–action pairs it uses the expected value, taking into account how likely each action is under the current policy. That is, consider the algorithm with the update rule
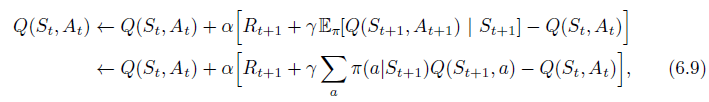 but that otherwise follows the schema of Q-learning. Given the next state,
S
t
+
1
S_{t+1}
St+1, this algorithm moves deterministically in the same direction as Sarsa moves in expectation, and accordingly it is called
E
x
p
e
c
t
e
d
Expected
Expected
S
a
r
s
a
Sarsa
Sarsa. Its backup diagram is shown in Figure 6.4.
but that otherwise follows the schema of Q-learning. Given the next state,
S
t
+
1
S_{t+1}
St+1, this algorithm moves deterministically in the same direction as Sarsa moves in expectation, and accordingly it is called
E
x
p
e
c
t
e
d
Expected
Expected
S
a
r
s
a
Sarsa
Sarsa. Its backup diagram is shown in Figure 6.4.

We indicate taking the maximum of these “next action” nodes with an arc across them.
- Expected Sarsa is more complex computationally than Sarsa but, in return, it eliminates the variance due to the random selection of A t + 1 A_{t+1} At+1. Given the same amount of experience we might expect it to perform slightly better than Sarsa, and indeed it generally does.
In (6.9), Expected Sarsa was used on-policy, but in general it might use a policy different from the target policy π pi π to generate behavior, in which case it becomes an off-policy algorithm.
- For example, suppose π pi π is the greedy policy while behavior is more exploratory; then Expected Sarsa is exactly Q-learning. In this sense Expected Sarsa subsumes and generalizes Q-learning while reliably improving over Sarsa.
- Except for the small additional computational cost, Expected Sarsa may completely dominate both of the other more-well-known TD control algorithms.
Maximization Bias and Double Learning
最大化偏差 与 双学习
All the control algorithms that we have discussed so far involve maximization in the construction of their target policies. For example,
- In Q-learning the target policy is the greedy policy given the current action values, which is defined with a max.
- In Sarsa the policy is often ε varepsilon ε-greedy, which also involves a maximization operation.
In these algorithms, a maximum over estimated values is used implicitly as an estimate of the maximum value, which can lead to a significant(显著的) positive bias.
- To see why, consider a single state s s s where there are many actions a a a whose true values, q ( s , a ) q(s, a) q(s,a), are all zero but whose estimated values, Q ( s , a ) Q(s, a) Q(s,a), are uncertain and thus distributed some above and some below zero. The maximum of the true values is zero, but the maximum of the estimates is positive, a positive bias. We call this m a x i m i z a t i o n maximization maximization b i a s bias bias.
Example 6.7: Maximization Bias Example
The small MDP shown inset in Figure 6.5 provides a simple example of how maximization bias can harm the performance of TD control algorithms.
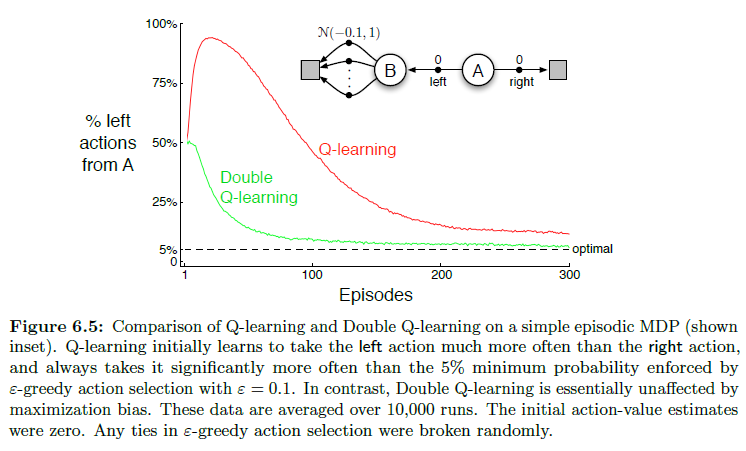
- The MDP has two non-terminal states A A A and B B B. Episodes always start in A A A with a choice between two actions, left and right. The right action transitions immediately to the terminal state with a reward and return of zero. The left action transitions to B B B, also with a reward of zero, from which there are many possible actions all of which cause immediate termination with a reward drawn from a normal distribution with mean −0.1 and variance 1.0. Thus, the expected return for any trajectory starting with left is −0.1, and thus taking left in state A A A is always a mistake.
- Nevertheless, our control methods may favor left because of maximization bias making B B B appear to have a positive value. Figure 6.5 shows that Q-learning with ε varepsilon ε-greedy action selection initially learns to strongly favor the left action on this example. Even at asymptote, Q-learning takes the left action about 5% more often than is optimal at our parameter settings ( ε = 0.1 , α = 0.1 varepsilon = 0.1, alpha = 0.1 ε=0.1,α=0.1, and γ = 1 gamma = 1 γ=1)
Are there algorithms that avoid maximization bias?
- To start, consider a bandit case in which we have noisy estimates of the value of each of many actions, obtained as sample averages of the rewards received on all the plays with each action. As we discussed above, there will be a positive maximization bias if we use the maximum of the estimates as an estimate of the maximum of the true values.
- One way to view the problem is that it is due to using the same samples (plays) both to determine the maximizing action and to estimate its value.
- Suppose we divided the plays in two sets and used them to learn two independent estimates, call them Q 1 ( a ) Q_1(a) Q1(a) and Q 2 ( a ) Q_2(a) Q2(a), each an estimate of the true value q ( a ) q(a) q(a), for all a ∈ A ain mathcal A a∈A. We could then use one estimate, say Q 1 Q_1 Q1, to determine the maximizing action A ∗ = a r g m a x a Q 1 ( a ) A^* = argmax_a Q_1(a) A∗=argmaxaQ1(a), and the other, Q 2 Q_2 Q2, to provide the estimate of its value, Q 2 ( A ∗ ) = Q 2 ( a r g m a x a Q 1 ( a ) ) Q_2(A^*) = Q_2(argmax_a Q_1(a)) Q2(A∗)=Q2(argmaxaQ1(a)). This estimate will then be unbiased in the sense that E [ Q 2 ( A ∗ ) ] = q ( A ∗ ) mathbb E[Q_2(A^*)] = q(A^*) E[Q2(A∗)]=q(A∗). We can also repeat the process with the role of the two estimates reversed to yield a second unbiased estimate Q 1 ( a r g m a x a Q 2 ( a ) ) Q_1(argmax_a Q_2(a)) Q1(argmaxaQ2(a)). This is the idea of d o u b l e double double l e a r n i n g learning learning.
- Note that although we learn two estimates, only one estimate is updated on each play; double learning doubles the memory requirements, but does not increase the amount of computation per step.
- The idea of double learning extends naturally to algorithms for full MDPs.
- For example, the double learning algorithm analogous to Q-learning, called Double Q-learning, divides the time steps in two, perhaps by flipping a coin on each step.
- If the coin comes up heads, the update is

- If the coin comes up tails, then the same update is done with Q 1 Q_1 Q1 and Q 2 Q_2 Q2 switched, so that Q 2 Q_2 Q2 is updated.
- The two approximate value functions are treated completely symmetrically. The behavior policy can use both action-value estimates. For example, an ε varepsilon ε-greedy policy for Double Q-learning could be based on the average (or sum) of the two action-value estimates.

Of course there are also double versions of Sarsa and Expected Sarsa.
Exercise 6.13
What are the update equations for Double Expected Sarsa with an
ε
varepsilon
ε-greedy target policy?
ANSWER
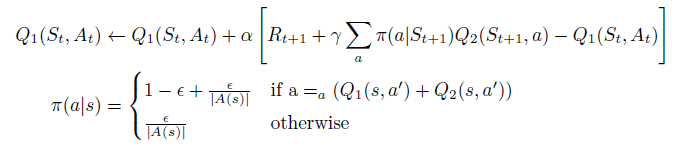
Games, Afterstates, and Other Special Cases
Afterstates: 后位状态
In this book we try to present a uniform approach to a wide class of tasks, but of course there are always exceptional tasks that are better treated in a specialized way.
- For example, our general approach involves learning an action-value function, but in Chapter 1 we presented a TD method for learning to play tic-tac-toe that learned something much more like a state-value function.
- If we look closely at that example, it becomes apparent that the function learned there is neither an action-value function nor a state-value function in the usual sense. A conventional state-value function evaluates states in which the agent has the option of selecting an action, but the state-value function used in tic-tac-toe evaluates board positions a f t e r after after the agent has made its move. Let us call these a f t e r s t a t e s afterstates afterstates, and value functions over these, a f t e r s t a t e afterstate afterstate v a l u e value value f u n c t i o n s functions functions.
Afterstates are useful when we have knowledge of an initial part of the environment’s dynamics but not necessarily of the full dynamics.
- For example, in games we typically know the immediate effects of our moves. We know for each possible chess move what the resulting position will be, but not how our opponent will reply. Afterstate value functions are a natural way to take advantage of this kind of knowledge and thereby produce a more efficient learning method.
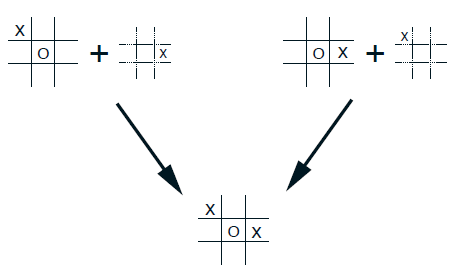
The reason it is more efficient to design algorithms in terms of afterstates is apparent from the tic-tac-toe example.
- A conventional action-value function would map from positions and moves to an estimate of the value. But many position—move pairs produce the same resulting position, as in the example below: In such cases the position–move pairs are different but produce the same “ a f t e r p o s i t i o n afterposition afterposition,” and thus must have the same value. A conventional action-value function would have to separately assess both pairs, whereas an afterstate value function would immediately assess both equally. Any learning about the position–move pair on the left would immediately transfer to the pair on the right.
- Afterstates arise in many tasks, not just games. For example, in queuing tasks there are actions such as assigning customers to servers, rejecting customers, or discarding information. In such cases the actions are in fact defined in terms of their immediate effects, which are completely known.
- It is impossible to describe all the possible kinds of specialized problems and corresponding specialized learning algorithms. However, the principles developed in this book should apply widely.
- For example, afterstate methods are still aptly described in terms of generalized policy iteration, with a policy and (afterstate) value function interacting in essentially the same way. In many cases one will still face the choice between on-policy and off-policy methods for managing the need for persistent exploration.
Exercise 6.14
Describe how the task of Jack’s Car Rental (Example 4.2) could be reformulated in terms of afterstates. Why, in terms of this specific task, would such a reformulation be likely to speed convergence?
ANSWER
We can focus the after-states about parking numbers at each day’s morning. It will be the whole result of yesterday’s actions. It will decrease the computation because we have many different ways of arranging cars but we will end up next morning the same number of cars at each locations.
最后
以上就是落后冰棍最近收集整理的关于RL(Chapter 6): Temporal-Difference Learning (TD learning) (时序差分学习)TD PredictionAdvantages of TD Prediction MethodsOptimality of TD(0)Sarsa: On-policy TD ControlQ-learning: Off-policy TD ControlExpected SarsaMaximization Bias and Double LearningGames,的全部内容,更多相关RL(Chapter内容请搜索靠谱客的其他文章。








发表评论 取消回复