leetcode 剑指 Offer 51. 数组中的逆序对

剑指 Offer 51. 数组中的逆序对
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

限制：

0 <= 数组长度 <= 50000

以下内容部分来自威威大佬：

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solution/bao-li-jie-fa-fen-zhi-si-xiang-shu-zhuang-shu-zu-b/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

我们进行一次归并排序，并在归并过程中计算逆序数，换句话说 逆序对是归并排序的副产物。
说明：理解这个算法需要对「归并排序」比较熟悉。掌握如果编写递归函数，每一次都一分为二拆分数组的子区间，然后在方法栈弹出的时候，一步一步合并两个有序数组，最后完成排序工作。

而计算逆序数就发生在排序的过程中，利用了「排序」以后数组的有序性。

利用「归并排序」计算逆序对，是非常经典的做法；
关键在于「合并两个有序数组」的步骤，利用数组的部分有序性，一下子计算出一个数之前或者之后元素的逆序的个数；
前面「分」的时候什么都不做，「合」的过程中计算「逆序对」的个数；
「排序」的工作是必要的，正是因为「排序」才能在下一轮利用顺序关系加快逆序数的计算，也能避免重复计算；
在代码实现上，只需要在「归并排序」代码的基础上，加上「逆序对」个数的计算，计算公式需要自己在草稿纸上推导。

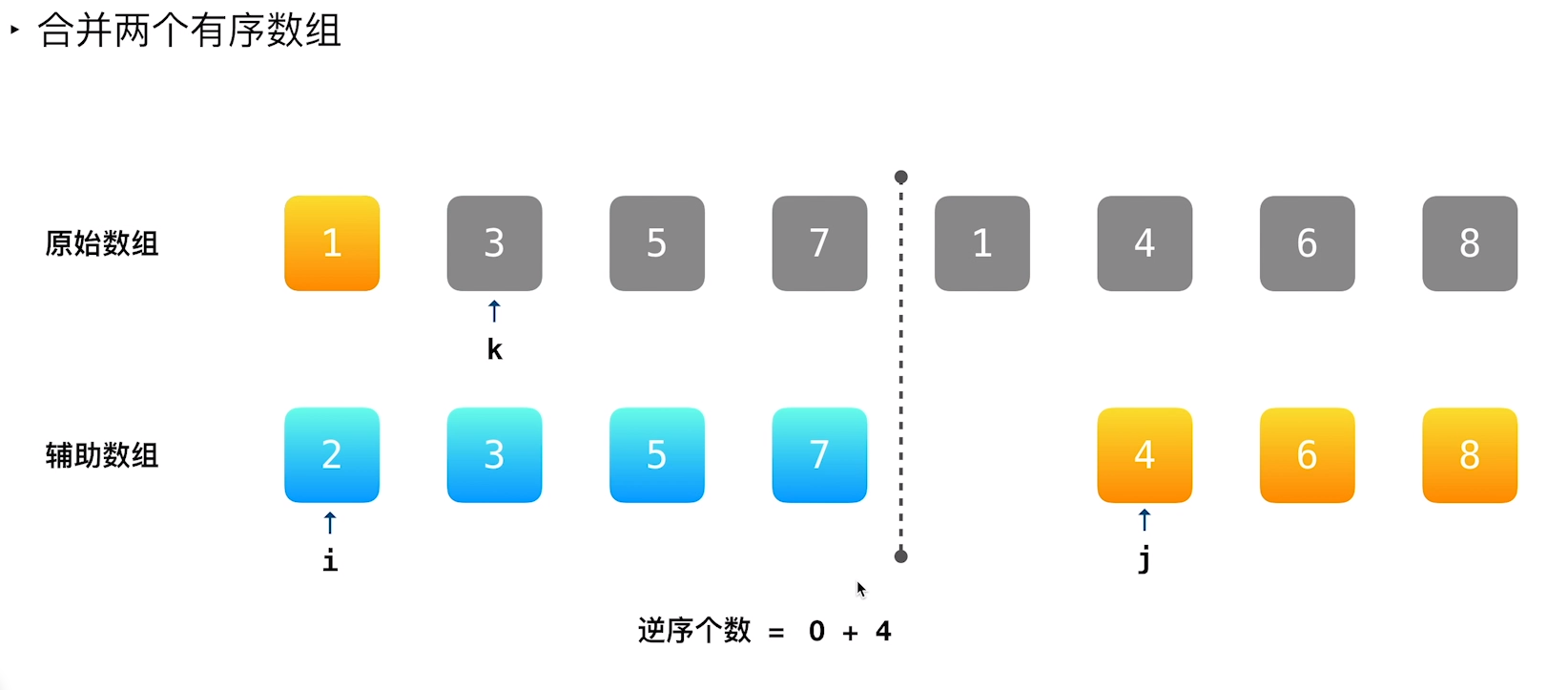
归并排序主要在归并的部分，部分代码如下：

def mergeTwo(nums1, nums2):
    res = []
    i = j = 0
    while i < len(nums1) and j < len(nums2):
        if nums1[i] < nums[j]:
            res.append(nums[i])
            i += 1
        else:
            res.append(nums[j])
            j += 1
    while i < len(nums1) :
        res.append(num[i])
        i += 1
    while j < len(nums1) :
        res.append(num[j])
        j += 1
    return res


作者：fe-lucifer
链接：https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solution/jian-dan-yi-dong-gui-bing-pai-xu-python-by-azl3979/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

由于是在并的过程中计算逆序的数量，所以一下几个点需要注意：

• 整个过程中使用的区间都是闭区间
• 在归并的比较部分，我们由于是要并成为一个递增的串，所以计算逆序的时候，应该右半部分的值在相同的情况下优先合并到临时的数组内
• 计算逆序数量的时候，我们都是通过左边部分剩余个数就是当前右边被抽走排序的值的逆序个数，这里左半部分的剩余个数为[mid - i - 1],其中mid是左边界，i 是指针， 两者之间的数的个数就是剩余的数量。
• 最后在拆分的时候，如果区间内部只有一个值，就直接返回，不需要排序。

class Solution:
    def reversePairs(self, nums: List[int]) -> int:
        self.cnt = 0

        def merge(nums, left, mid, right, temp):#这里是闭区间
            i, j = left, mid+1#i 指针左边， j 指针右边
            while i <= mid and j <= right:
                if nums[i] <= nums[j]:#这里注意是小于等于，因为我们优先合并右边的区间就算逆序
                    temp.append(nums[i])
                    i += 1
                else:
                    temp.append(nums[j])
                    self.cnt += (mid - i + 1)
                    j += 1
            while i <= mid:#右边合并完毕
                temp.append(nums[i])
                i += 1
            while j <= right:#左边合并完毕
                temp.append(nums[j])
                j += 1
            
            for i in range(len(temp)):#辅助数组赋值回原数组
                nums[left+i] = temp[i]
            temp.clear()#清除当前的辅助列表

        def mergeSort(nums, left, right, temp):
            if left >= right: return 
            mid = left + (right - left) // 2
            mergeSort(nums, left, mid, temp)
            mergeSort(nums, mid+1, right, temp)
            merge(nums, left, mid, right, temp)
        mergeSort(nums, 0, len(nums)-1, [])
        # print(nums)
        return self.cnt

最后

以上就是自信纸鹤为你收集整理的leetcode 剑指 Offer 51. 数组中的逆序对的全部内容，希望文章能够帮你解决leetcode 剑指 Offer 51. 数组中的逆序对所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。