Generative Modeling by Estimating Gradients of the Data Distribution论文阅读摘要引文基于分数的生成建模/Score-based generative modeling基于分数的生成建模的挑战噪声条件分数网络/NCSN:学习和推理实验相关工作结论

论文链接：Generative Modeling by Estimating Gradients of the Data Distribution

摘要

本论文引入了一种新的生成模型，该模型使用分数匹配估计的数据分布梯度通过朗之万动力学生成样本。由于当数据驻留在低维流形上时，梯度可能定义不清且难以估计，用不同水平的高斯噪声扰动数据，并联合估计相应的分数，即在所有噪声水平下扰动数据分布的梯度向量场。对于采样，提出了一种退火的朗之万动力学，在该动力学中，随着采样过程越来越接近数据流形，使用了相应于逐步降低噪声水平的梯度。本论文框架允许灵活的模型架构，在训练期间不需要采样或使用对抗方法，并提供了一个学习目标，可以用于原则性模型比较。本论文模型产生的样本可与MNIST、CelebA和CIFAR-10数据集上的GANs相媲美，在CIFAR-10上获得了SOTA的inception分数，8.87。此外，结果证明本文模型可通过图像修复实验能学习有效的表示。

引文

生成模型在机器学习中有很多应用。举几个例子，它们被用于生成高保真图像，合成真实的语音和音乐片段，提高半监督学习的性能，检测对抗例子和其他异常数据，模仿学习，以及探索强化学习中有前景的状态。最近的进展主要由两种方法驱动:基于似然的方法和生成对抗网络(GAN)。前者使用对数似然(或一个合适的替代项)作为训练目标，而后者使用对抗训练来最小化模型和数据分布之间的$f$散度或积分概率度量。

尽管基于似然的模型和GANs已经取得了巨大的成功，但它们都有一些内在的局限性。例如，基于似然的模型要么必须使用专门的架构来构建规范化的概率模型(如自回归模型、流模型)，要么使用替代损失(如在VAE中使用的ELBO，在基于能量的模型中使用的对比散度)进行训练。GANs避免了基于似然模型的一些局限性，但由于对抗训练过程，它们的训练可能不稳定。此外，GAN目标不适合评价和比较不同的GAN模型。虽然生成建模存在其他目标，如噪声对比估计和最小概率流，但这些方法通常只适用于低维数据。

本文探索了一种基于对数数据密度(Stein)分数(即输入数据点的对数密度函数的梯度)的估计和采样来生成建模的新原理。这是一个向量场，指向对数数据密度增长最大的方向；使用经过分数匹配训练的神经网络从数据中学习这个向量场。然后使用Langevin Dynamics生成样本，其近似工作方式是将随机初始样本沿着分数的(估计的)矢量场逐渐移动到高密度区域。然而，这种方法有两个主要挑战。首先，如果数据主要分布在低维流形上–就像许多现实世界的数据集经常假定的那样–分数在环境空间中是未定义的，并且分数匹配将无法提供一致的分数估计器。其次，在远离流形的低数据密度区域，训练数据的稀缺阻碍了分数估计的准确性，并减慢了朗之万动力学采样的混合。由于朗之万动力学通常会在数据分布的低密度区域进行初始化，因此这些区域的不准确分数估计会对采样过程产生负面影响。此外，混合可能很困难，因为需要穿越低密度区域来在分布模式之间转换。

为了应对这两个挑战，本文建议用不同幅度的随机高斯噪声来扰动数据。添加随机噪可确保生成的分布不会塌陷到低维流形。较大的噪声水平将在原始(未受干扰的)数据分布的低密度区域产生样本，从而改进得分估计。至关重要的是，本文训练了一个以噪声水平为条件的单一得分网络，并估计了所有噪声幅度的得分。然后，提出退火朗之万动力学，其中最初使用对应于最高噪声水平的分数，并逐渐降低噪声水平，直到它足够小，无法与原始数据分布区分。采样策略的灵感来自模拟退火法，它启发式地改进了多模态场景的优化。

本文方法有几个可取的特性。首先，训练目标对于分数网络几乎所有参数化都是可处理的，而不需要特殊的约束或架构；并且可以在训练过程中不使用对抗训练、MCMC采样或其他近似方法进行优化。目标也可用于定量比较同一数据集上的不同模型。实验证明了本文方法对MNIST, CelebA和CIFAR-10的有效性。生成的样本看起来可与现有基于似然的模型和GANs生成的样本相媲美。在CIFAR-10上，本文模型在无条件生成模型中达到了新SOTA的inception分数，8.87；并实现了具有竞争力的FID得分25.32。同时，本文模型通过图像修复实验数据能学习到有意义的表征。

基于分数的生成建模/Score-based generative modeling

假设数据集来自未知数据分布$p_{data}(x)$，由样本 { x i ∈ R D } i = 1 N lbrace x_i in R^D rbrace^N_{i=1} {xi​∈RD}i=1N​；定义概率密度$p(x)$的得分为${\nabla }_x\log p(x)$。分数网络$S_{\theta }:R^D\to R^D$是由$\theta$参数化的神经网络，其被训练去估计$p_{data}(x)$的得分。生成模型的目标是使用数据集学习一个模型，进而可以从$p_{data}(x)$分布中生成新的样本。基于分数的生成建模框架有两个组成部分:分数匹配(score matching)和朗格万动力学(Langevin dynamics)。

用于分数估计的分数匹配/Score matching for score estimation

分数匹配最初设计用于“基于来自未知数据分布样本数据”学习非规范化的统计模型。遵循Sliced Score Matching: A Scalable Approach to Density and Score Estimation，本文将其重新用于分数估计。通过分数匹配，可以直接训练分数网络$S_{\theta }(x)$来估计${\nabla }_x\log p_{data}(x)$，而不需要先训练模型来估计$p_{data}(x)$。与典型的分数匹配方法不同，本文选择不使用基于能量模型的梯度作为分数网络，以避免高阶梯度带来的额外计算。目标是最小化$\frac{1}{2}{E}_{p_{data}}[||S_{\theta }(x)-{\nabla }_x\log p_{data}(x)|{|}_2^2]$，可被证明等价于下面的常数
$$E_{p_{data}(x)}[tr({\nabla }_x{S}_{\theta }(x))+\frac{1}{2}||S_{\theta }(x)|{|}_2^2],\text{\hspace{1em}(1)}$$
其中${\nabla }_x{S}_{\theta }(x)$表示$S_{\theta }(x)$的雅可比矩阵。如Sliced Score Matching论文中所述，在某些规律性条件下，公式3的最小值(记为$S_{{\theta }^{\ast }}(x)$)几乎肯定满足$S_{{\theta }^{\ast }}(x)={\nabla }_x\log p_{data}(x)$。实际上，可以使用数据样本快速估计公式1中$p_{data}(x)$的期望。然而，由于$tr({\nabla }_x{S}_{\theta }(x))$的计算，分数匹配无法扩展到深层网络和高维数据。下面将讨论两种流行的大规模分数匹配方法。

Denoising score matching

去噪分数匹配是分数匹配的一种变体，完全规避计算$tr({\nabla }_x{S}_{\theta }(x))$。它先使用预先指定的噪声扰动数据$x$得到分布$q_{\sigma }(\tilde{x}|x)$，然后使用分数匹配估计受扰动数据分布的得分$q_{\sigma }(\tilde{x})\triangleq \int q_{\sigma }(\tilde{x}|x)p_{data}(x)dx$。目标被证明等价于以下内容：
$$\frac{1}{2}{E}_{q_{\sigma }(\tilde{x}|x)p_{data}(x)}[||S_{\theta }(\tilde{x})-{\nabla }_{\tilde{x}}\log q_{\sigma }(\tilde{x}|x)|{|}_2^2].\text{\hspace{1em}(2)}$$
如Denoising score matching论文中所述，最小化公式2的最优分数网络(记为$S_{{\theta }^{\ast }}(x)$)几乎肯定满足$S_{{\theta }^{\ast }}(x)={\nabla }_x\log q_{\sigma }(x)$。然而，只有当噪声足够小时，$S_{{\theta }^{\ast }}(x)={\nabla }_x\log q_{\sigma }(x)\approx {\nabla }_x\log p_{data}(x)$才成立。

Sliced score matching

切片分数匹配使用随机投影来近似分数匹配中的$tr({\nabla }_x{S}_{\theta }(x))$。优化目标是
$$E_{p_v}{E}_{p_{data}}[v^T{\nabla }_x{S}_{\theta }(x)v+\frac{1}{2}||S_{\theta }(x)|{|}_2^2],\text{\hspace{1em}(3)}$$
其中$p_v$是随机向量的一个简单分布，例如，多元标准正态分布。Sliced score matching论文中表明，$v^T{\nabla }_x{S}_{\theta }(x)v$可以通过前向模式自动微分有效地计算。与估计扰动数据分数的去噪分数匹配不同，切片分数匹配为原始未受干扰数据分布提供分数估计，但由于前向模式自微分，需要进行大约四倍计算量。

朗之万动力学采样/Sampling with Langevin dynamics

朗之万动力学仅使用得分函数${\nabla }_x\log p(x)$从概率密度$p(x)$生成样本。给定一个固定步长$ϵ>0$，初始值${\tilde{x}}_0\sim \pi (x)$，其中$\pi$是先验分布，Langevin方法递归地计算以下内容
$${\tilde{x}}_t={\tilde{x}}_{t-1}+\frac{ϵ}{2}{\nabla }_x\log p({\tilde{x}}_{t-1})+\sqrt{ϵ}{z}_t\text{\hspace{1em}(4)}$$
其中$z_t\sim N(0,1)$。当$ϵ\to 0,T\to \infty$时，${\tilde{x}}_T$的分布等于$p(x)$；此时在一些规律性条件下，${\tilde{x}}_T$成为$p(x)$的精确样本。当当$ϵ>0,T<\infty$时，需要一个Metropolis-Hastings更新来纠正公式4的误差，但在实践中通常可以忽略。本工作假设当$ϵ$较小且$T$很大时，此误差可以忽略不计。

注意，从公式4中采样只需要分数函数${\nabla }_x\log p(x)$。因此，为了从$p_{data}(x)$中获取样本，可以首先训练分数网络，使$S_{\theta }(x)\approx {\nabla }_x\log p_{data}(x)$，然后基于$S_{\theta }(x)$用朗之万动力学近似获取样本。这是本文基于分数的生成建模框架的关键思想。

基于分数的生成建模的挑战

流形假设/manifold hypothesis

流形假设指出，现实世界中的数据往往集中在嵌入高维空间(又称环境空间)的低维流形上。这一假设在许多数据集上都是经验成立的，并已成为多种学习的基础。在流形假设下，基于分数的生成模型将面临两个关键困难。首先，由于分数${\nabla }_x\log p_{data}(x)$是在环境空间中取的梯度，当$x$被限制在低维流形时，它是未定义的。其次，分数匹配目标公式1仅当数据分布的支持是整个空间时才提供一致的分数估计器，当数据驻留在低维流形上时，将不一致。

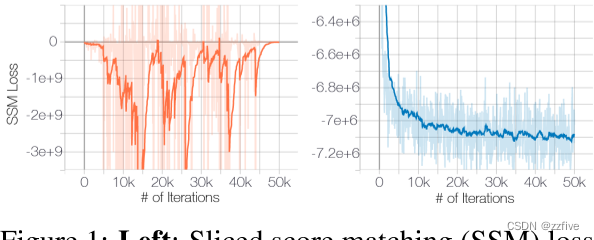
流形假设对分数估计的负面影响从图1可以清楚地看出，训练ResNet（详见附录 B.1）来估计CIFAR-10上的数据分数。为了快速训练和直观地估计数据分数，使用切片分数匹配目标(公式3)。如图1(左)所示，在原始CIFAR-10图像上进行训练时，切片分数匹配损失首先减小，然后不规则波动。相比之下，如果用一个小的高斯噪声扰动数据（使得扰动数据分布对$R^D$完全支持），损失曲线将收敛，如图1(右)。注意，对于像素值在[0, 1]范围内的图像，施加的高斯噪声$N(0,0.0001)$非常小，人眼几乎无法区分。

低数据密度区域

低密度区域的数据稀缺会给分数匹配的分数估计和朗日万动态的MCMC采样带来困难。

分数匹配的不准确分数估计

在低数据密度区域，由于缺乏数据样本，分数匹配可能没有足够的证据来准确估计分数函数。为了了解这一点，回顾前文提到的分数匹配中最小化分数估计平方误差的期望，即$\frac{1}{2}{E}_{p_{data}}[||S_{\theta }(x)-{\nabla }_x\log p_{data}(x)|{|}_2^2]$。实际上，关于数据分布的期望总是由独立同分布的样本 { x i } i = 1 N ∼ i . i . d p d a t a ( x ) lbrace x_i rbrace^N_{i=1} overset{i.i.d}sim p_{data}(x) {xi​}i=1N​∼i.i.dpdata​(x)估计的。考虑任务使$p_{data}(R)\approx 0$的区域$R\in R^D$。大多数情况下 { x i } i = 1 N ∩ R = ∅ lbrace x_i rbrace^N_{i=1} cap R = emptyset {xi​}i=1N​∩R=∅，分数匹配将没有足够的数据样本来准确估计出对于$x\in R$的${\nabla }_x\log p_{data}(x)$。为了证明这种负面影响，在图2中提供了一个实验的结果(详见附录B.1)，其中使用切片分数匹配来估计混合高斯$p_{data}=\frac{1}{5}N((-5,-5),I)+\frac{4}{5}N((5,5),I)$的得分。如图2所示，只有在$p_{data}$的模态附近，即数据密度较高的情况下，分数估计才可靠。

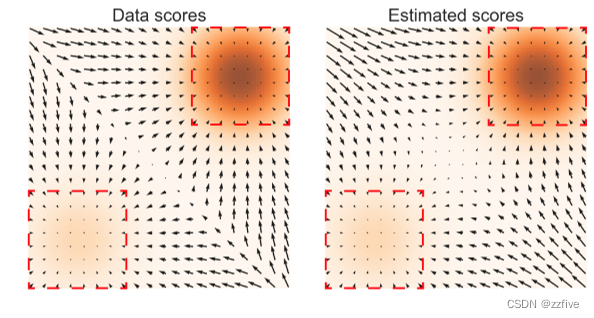
图2 左：${\nabla }_x\log p_{data}(x)$；右：$S_{\theta }(x)$。数据密度$p_{data}(x)$使用橙色颜色图进行编码：较深的颜色意味着更高的密度；红色矩形突出显示${\nabla }_x\log p_{data}(x)\approx S_{\theta }(x)$的区域。

朗之万动力学的缓慢混合

当两种数据分布模式由低密度区域分离时，朗之万动力学无法在合理的时间内正确恢复这两种模式的相对权重，因此可能无法收敛到真实分布。对这一点的分析很大程度上受到A connection between score matching and denoising autoencoders的启发，其在分数匹配的密度估计的背景下分析了相同的现象。

考虑一个混合分布$p_{data}(x)=\pi p_1(x)+(1-\pi )p_2(x)$，其中$p_1(x)$和$p_2(x)$是具有不相交支持的归一化分布，$\pi \in (0,1)$。在$p_1(x)$的支持下，${\nabla }_x\log p_{data}(x)={\nabla }_x(\log \pi +\log p_1(x))={\nabla }_x\log p_1(x)$，在$p_2(x)$的支持下，${\nabla }_x\log p_{data}(x)={\nabla }_x(\log (1-\pi )+\log p_2(x))={\nabla }_x\log p_2(x)$。在这两种情况下，分数${\nabla }_x\log p_{data}(x)$不依赖于$\pi$。由于朗之万动力学使用${\nabla }_x\log p_{data}(x)$从$p_{data}(x)$中采样，因此得到的样本不依赖于$\pi$。实际上，当不同的模式有近似不相交的支持时，该分析也成立——它们可能共享相同的支持，但是由小数据密度的区域连接。在这种情况下，朗之万动力学理论上可以产生正确的样本，但可能需要非常小的步长和非常大量的步骤来混合。

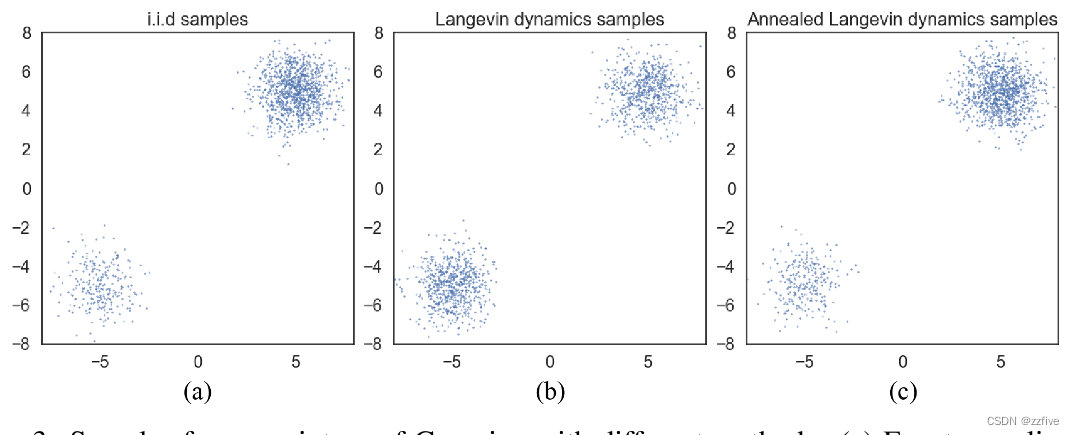
为了验证该分析，本文测试了前文中使用的相同高斯混合的Langevin动态采样，并得到图3中的结果。当使用Langevin动态采样时，使用Ground Truth的分数。将图3(b)与(a)进行比较，很明显朗之万动力学的样本在两种模式之间具有不正确的相对密度，正如分析所预测的那样。

噪声条件分数网络/NCSN:学习和推理

本文观察到，使用随机高斯噪声扰动数据使数据分布更适合基于分数的生成建模。首先，由于高斯噪声分布的支持是整个空间，使得受扰动数据不限于低维流形，避免了流形假设的困难并使分数估计明确定义。其次，大高斯噪声具有在原始未受干扰的数据分布中填充低密度区域的效果；因此，分数匹配可能会得到更多的训练信号来提高分数估计。此外，通过使用多个噪声水平，可以获得收敛到真实数据分布的噪声扰动分布序列。可以通过本着模拟退火的精神利用这些中间分布和退火重要性抽样来提高朗之万动力学在多峰分布上的混合速率。

基于这种直觉，通过以下方法改进基于分数的生成建模：1)使用不同级别的噪声扰动数据；2)通过训练单一条件分数网络，同时估计出与所有噪声级别相对应的分数。经过训练后，在使用朗之万动力学生成样本时，首先使用大噪声对应的分数，然后逐步将噪声水平退火。这有助于平稳地将大噪声水平的好处转移到低噪声水平，在低噪声水平下，扰动数据几乎无法与原始数据区分开来。下文详细阐述本文方法的细节，包括分数网络的体系结构、训练目标和朗格万动力学的退火计划。

噪声条件分数网络/NCSN

设置 { σ i } i = 1 L lbrace sigma_i rbrace^L_{i=1} {σi​}i=1L​为满足$\frac{{\sigma }_1}{{\sigma }_2}=\cdot \cdot \cdot =\frac{{\sigma }_{L-1}}{{\sigma }_L}>0$的正等比级数序列。设置$q_{\sigma }(x)\triangleq \int p_{data}(t)N(x|t,{\sigma }^{2}I)dt$表示扰动数据分布。本文选择噪声水平 { σ i } i = 1 L lbrace sigma_i rbrace^L_{i=1} {σi​}i=1L​例如${\sigma }_1$足够大，以减轻前文中讨论的困难，而${\sigma }_L$足够小，以减少对数据的影响。目标是训练一个条件分数网络来联合估计所有扰动数据分布的分数，即 ∀ σ ∈ { σ i } i = 1 L : S θ ( x , σ ) ≈ ∇ x log ⁡ q σ ( x ) ∀ σ ∈ lbraceσ_i rbrace^L_{i=1}: S_θ(x,σ) ≈ ∇_x log q_σ(x) ∀σ∈{σi​}i=1L​:Sθ​(x,σ)≈∇x​logqσ​(x)。注意当$x\in R^D$时，$S_{\theta }(x,\sigma )\in R^D$，称$S_{\theta }(x,\sigma )$为噪声条件分数网络(NCSN)。

与基于似然的生成模型和GANs类似，模型体系结构的设计对于生成高质量的样本起着重要作用。本工作主要关注对图像生成有用的体系结构，而将其他领域的体系结构设计留作以后的工作。由于噪声条件分数网络$S_{\theta }(x,\sigma )$的输出与输入图像$x$具有相同的形状，从成功的图像密集预测模型架构(例如，语义分割)中获得灵感。在实验中，本文提出的模型$S_{\theta }(x,\sigma )$结合了U-Net的架构设计和dilated/atrous卷积，这两者在语义分割中都被证明非常成功。此外，在分数网络中采用了实例归一化，灵感来自于它在一些图像生成任务中的优越性能；并且使用条件实例归一化的修改版本来提供对${\sigma }_i$的条件。关于模型架构的更多细节可以在附录A中找到。

通过分数匹配学习NCSN

切片分数匹配和去噪分数匹配都可以训练NCSN。本文采用去噪分数匹配，因为它略快，自然适合估计受噪声干扰数据分布的分数的任务。然而，在此强调，用经验的切片分数匹配训练的NCSN可以与用去噪分数匹配训练的NCSN一样好。选择噪声分布为$q_{\sigma }(\tilde{x}|x)=N(\tilde{x}|x,{\sigma }^{2}I)$，因此${\nabla }_{\tilde{x}}\log q_{\sigma }(\tilde{x}|x)=-\frac{(\tilde{x}-x)}{{\sigma }^2}$。给定一个$\sigma$，去噪分数匹配目标(公式2)如下
$$l(\theta ;\sigma )\triangleq \frac{1}{2}{E}_{p_{data}(x)}{E}_{\tilde{x}\sim N(x,{\sigma }^{2}I)}[||S_{\theta }(\tilde{x},\sigma )+\frac{\tilde{x}-x}{{\sigma }^2}|{|}_2^2].\text{\hspace{1em}(5)}$$

然后，对所有 σ ∈ { σ i } i = 1 L σ∈lbraceσ_irbrace^L_{i=1} σ∈{σi​}i=1L​，将公式5合并得到一个统一的目标：
L ( θ ; { σ i } i = 1 L ) ≜ 1 L ∑ i = 1 L λ ( σ i ) l ( θ ; σ i ) , (6) L(theta;lbraceσ_irbrace^L_{i=1}) triangleq frac{1}{L}sum^L_{i=1}lambda(sigma_i)l(theta;sigma_i), tag{6} L(θ;{σi​}i=1L​)≜L1​i=1∑L​λ(σi​)l(θ;σi​),(6)
其中$\lambda ({\sigma }_i)>0$是依赖于${\sigma }_i$的一个系数函数。假设$S_{\theta }(x,\sigma )$有足够的能力，对于所有$i\in 1,2，\cdot \cdot \cdot ，L$，当且仅当$S_{{\theta }^{\ast }}(x,{\sigma }_i)={\nabla }_x\log q_{{\sigma }_i}(x)$，能使公式6最小化，因为公式6是$L$个去噪分数匹配目标的锥形组合。

$\lambda (\cdot )$可以有很多可能的选择。理想情况下，希望$\lambda ({\sigma }_i)l(\theta ;{\sigma }_i)$对于所有 { σ i } i = 1 L lbraceσ_irbrace^L_{i=1} {σi​}i=1L​大致具有相同的数量级。根据经验，观察到当分数网络训练到最优状态时，大约有$||S_{\theta }(x,\sigma )|{|}_2\propto 1/\sigma$。这启发本文选择$\lambda (\sigma )={\sigma }^2$。因为在这个选择下，有$\lambda (\sigma )l(\theta ;\sigma )={\sigma }^{2}l(\theta ;\sigma )=\frac{1}{2}E[||\sigma S_{\theta }(\tilde{x},\sigma )+\frac{\tilde{x}-x}{\sigma }|{|}_2^2]$。因为$\frac{\tilde{x}-x}{\sigma }\sim N(0,I),||\sigma S_{\theta }(x,\sigma )||\propto 1$，很容易得出$\lambda ({\sigma }_i)l(\theta ;{\sigma }_i)$的大小不依赖于$\sigma$。

在此强调目标公式6不需要对抗训练，没有代理损失，并且在训练期间没有从分数网络中采样（如与对比散度不同）。此外，它不需要$S_{\theta }(x,\sigma )$具有特殊的架构，易于处理。此外，当$\lambda (\cdot )$和 { σ i } i = 1 L lbraceσ_irbrace^L_{i=1} {σi​}i=1L​固定时，可用于定量比较不同的NCSN。

基于退火朗之万动力学的NCSN推理

在训练了NCSN:$S_{\theta }(x,\sigma )$之后，提出了一种采样方法——退火朗之万动力学(算法1)去生成的样本，受模拟退火和退火重要性采样的启发。如算法1所示，开始退火的Langevin动力学采样，通过从某些固定的先验分布初始化样本进行，如均匀噪声。然后，运行朗之万动力学从步长为${\alpha }_1$的$q_{{\sigma }_1}(x)$中采样。接下来，运行朗之万动力学从$q_{{\sigma }_2}(x)$中采样，从先前模拟的最终样本开始，并使用减小的步长${\alpha }_2$。以这种方式继续，使用$q_{{\sigma }_{i-1}}(x)$的Langevin动力学的最终样本作为$q_{{\sigma }_i}(x)$的 Langevin 动态的初始样本，并以${\alpha }_i=ϵ\cdot {\sigma }_i^2/{\sigma }_L^2$逐步调整步长${\alpha }_i$。最后，运行朗之万动力学从$q_{{\sigma }_L}(x)$中采样，当${\sigma }_L\approx 0$时接近 $p_{data}(x)$。

由于分布 { q σ i } i = 1 L lbrace q_{σ_i} rbrace^L_{i=1} {qσi​​}i=1L​都受到高斯噪声的干扰，因此它们支持跨越整个空间并且它们的分数是明确定义的，避免了流形假设的困难。当${\sigma }_1$足够大时，$q_{{\sigma }_1}(x)$的低密度区域变小，模态变得不那么孤立。如前所述，这可以使分数估计更准确，并且朗之万动力学的混合更快。因此，可以假设朗之万动力学为 $q_{{\sigma }_1}(x)$产生良好的样本。这些样本可能来自$q_{{\sigma }_1}(x)$的高密度区域，这意味着它们也可能位于$q_{{\sigma }_2}(x)$的高密度区域，因为$q_{{\sigma }_1}(x)$和$q_{{\sigma }_2}(x)$彼此之间只有轻微差异。由于分数估计和朗之万动力学在高密度区域表现更好，因此来自$q_{{\sigma }_1}(x)$的样本将作为$q_{{\sigma }_2}(x)$的Langevin动力学的良好初始样本。类似地，$q_{{\sigma }_{i-1}}(x)$为$q_{{\sigma }_i}(x)$提供了良好的初始样本，最后从$q_{{\sigma }_L}(x)$中获得高质量样本。

根据算法1中的${\sigma }_i$，可以有多种可能的调整${\alpha }_i$的方法。本文的选择是${\alpha }_i\propto {\sigma }_i^2$，其目的是确定朗之万动力学中信噪比$\frac{{\alpha }_i{S}_{\theta }(x,{\sigma }_i)}{2{\sqrt{\alpha }}_{i}z}$的大小。注意，$E[||\frac{{\alpha }_i{S}_{\theta }(x,{\sigma }_i)}{2{\sqrt{\alpha }}_{i}z}|{|}_2^2]\approx E[\frac{{\alpha }_i||S_{\theta }(x,{\sigma }_i)|{|}_2^2}{4}]\propto \frac{1}{4}E[||{\sigma }_i{S}_{\theta }(x,{\sigma }_i)|{|}_2^2]$。回想一下，根据经验发现当分数网络接近最优时，$||S_{\theta }(x,\sigma )|{|}_2\propto 1/\sigma$，在这种情况下，$E[||{\sigma }_i{S}_{\theta }(x,{\sigma }_i)|{|}_2^2]\propto 1$。因此，$||\frac{{\alpha }_i{S}_{\theta }(x,{\sigma }_i)}{2{\sqrt{\alpha }}_{i}z}|{|}_2\propto \frac{1}{4}E[||{\sigma }_i{S}_{\theta }(x,{\sigma }_i)|{|}_2^2]\propto \frac{1}{4}$，不依赖${\sigma }_i$。

为了证明退火朗之万动力学的有效性，提供了一个示例，其目标是仅使用分数从具有两种具有良好分离模式的高斯混合中采样。将算法1应用于前文中使用的高斯混合样本。在实验中，选择 { q σ i } i = 1 L lbrace q_{σ_i} rbrace^L_{i=1} {qσi​​}i=1L​作为几何级数序列，其中$L=10,{\sigma }_1=10,{\sigma }_{10}=0.1$。结果如图3所示，对比图中b、c，退火朗格万动力学正确地恢复了两种模态之间的相对权重，而标准朗格万动力学则失败了。

实验

NCSN能够在几个常用的图像数据集上生成高质量的图像样本。此外，NCSN可通过图像修复实验学习到合理的图像表征。

设置

使用MNIST、CelebA和CIFAR-10数据集进行实验。对于CelebA，图像首先被中心裁剪为140 × 140，然后调整为32 × 32。所有的图像都被重新缩放，使像素值在[0，1]。选择$L=10$个不同的标准差，使 { q σ i } i = 1 L lbrace q_{σ_i} rbrace^L_{i=1} {qσi​​}i=1L​是一个几何数列，${\sigma }_1=1，{\sigma }_{10}=0.01$。注意，对于图像数据，$\sigma =0.01$的高斯噪声几乎无法被人眼区分。当使用退火朗日万动力学进行图像生成时，选择$T=100,ϵ=2\times 10^{-5}$，并使用均匀噪声作为初始样本。结果表明，$T$的选择具有鲁棒性，$ϵ$在$5\times 10^{-6}\to 5\times 10^{-5}$之间一般适用。在附录A和B中提供了关于模型架构和设置的更多细节。

图片生成

图5展示了MNIST、CelebA和CIFAR-10退火Langevin动力学的生成样本。从样本中可以看出，生成的图像与现代基于似然的模型和GANs的图像具有更高或相当的质量。为了直观地了解退火朗之万动力学的过程，在图4中提供了中间样本，其中每一行显示了样本如何从纯随机噪声演变为高质量图像。本文的方法的更多样本可以在附录C中找到，展示了附录C.2中训练数据集中生成的图像的最近邻居，以证明NCSN不是简单地记忆训练图像。为了表明联合学习多个噪声水平的条件分数网络并使用退火朗格万动力学的重要性，将其与只考虑一个噪声水平 { σ 1 = 0.01 } lbrace σ_1 = 0.01rbrace {σ1​=0.01}并使用原生朗之万动力学抽样方法的基线方法进行比较。尽管这个小的附加噪声有助于规避流形假设的困难(如图1所示，如果不添加噪声将完全失败)，但它还不足以提供低数据密度区域的分数信息。因此，该基线无法生成合理的图像，如附录C.1中的样本所示。

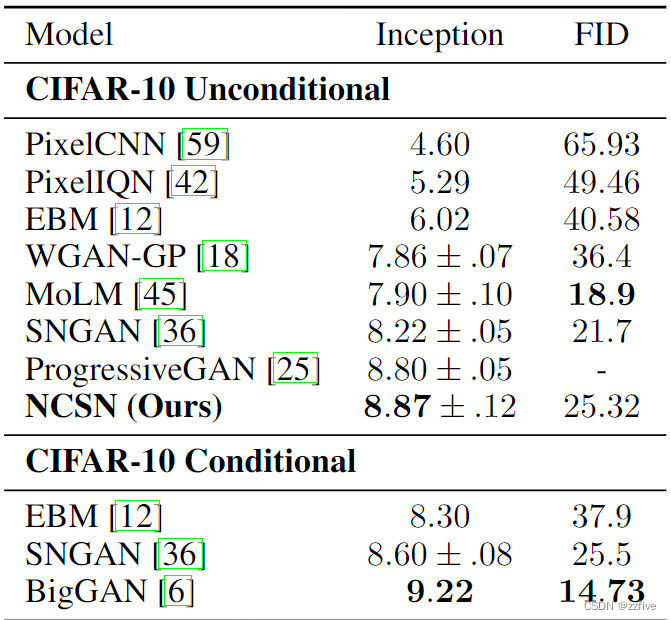
对于定量评估，在表1中报告了CIFAR-10上的inception和FID分数。作为无条件模型，实现了8.87的SOTA的inception分数，甚至优于有类别条件生成模型的大多数报告值。在CIFAR-10上的FID分数25.32也可与顶级现有模型相媲美，例如SNGAN。省略了MNIST和CelebA的分数，因为这两个数据集的分数没有被广泛报道，不同的预处理(例如CelebA的中心裁剪大小)可能导致数字不能直接比较。

图像修复

图6证明了本文的分数网络学习了可泛化和语义有意义的图像表示，使其能够产生不同的图像修复。请注意，之前的一些模型，如PixelCNN，只能以光栅扫描顺序估算图像。相比之下，本文方法可以通过对退火朗之万动力学过程的简单修改自然地处理任意形状遮挡的图像(详见附录B.3)。在附录 C.5 中提供了更多图像修复结果。

相关工作

本文方法与学习马尔可夫链的转换算子来生成样本的方法有一些相似之处。例如，生成随机网络(GSN)使用去噪自编码器训练一个平衡分布与数据分布匹配的马尔可夫链。类似地，本文方法训练Langevin动力学中使用的分数函数从数据分布中采样。然而，GSN通常从非常接近训练数据点的链开始，因此要求链在不同模式之间快速转换。相比之下，退火朗之万动力学是从非结构化噪声初始化的。非平衡热力学(NET)使用规定的扩散过程将数据缓慢转换为随机噪声，然后通过训练逆扩散来学习反转此过程。然而，NET不是很可扩展，因为它需要扩散过程有非常小的步骤，并且需要在训练时以数千个步骤模拟链。

以前的方法，如融合训练(IT)和变分行走(VW)也采用了不同的噪声水平/温度来训练马尔可夫链的过渡算子。IT和VW(以及NET)通过最大化适当边际似然的证据下限来训练他们的模型。在实践中，它们往往会产生模糊图像样本，类似于变分自动编码器。相比之下，本文目标是基于分数匹配而不是可能性，可以生成与GAN相当的图像。

有几个结构差异进一步将本文方法与上面讨论的以前的方法区分开来。首先，在训练期间不需要从马尔可夫链中采样。相比之下，GSNs的回溯过程需要链的多次运行来生成“负样本”；
包括NET、IT和VW在内的其他方法也需要为每个输入模拟马尔可夫链来计算训练损失。这种差异使得本文方法对于训练深度模型更有效和可扩展。其次，本文训练和采样方法相互解耦。对于分数估计，可以使用切片和去噪分数匹配。对于采样，任何基于分数的方法都适用，包括朗之万动力学和(可能)哈密顿蒙特卡罗。本文框架允许分数估计器和（基于梯度的）采样方法的任意组合，而大多数以前的方法将模型与特定马尔可夫链联系起来。最后，本文方法可以通过使用基于能量的模型的梯度作为分数模型来训练基于能量的模型 (EBM)。相比之下，尚不清楚以前学习马尔可夫链转换算子的方法如何直接用于训练EBMs。

分数匹配最初是为学习EBMs而提出的。然而，许多现有的基于分数匹配的方法要么不可扩展，要么无法产生与VAE或GANs相当质量的样本。为了在训练基于深度能量的模型方面获得更好的性能，最近的一些工作采用了对比散度，并建议用朗之万动力学对训练和测试进行采样。然而，与本文方法不同，对比散度在训练期间使用Langevin动力学的计算代价高昂的过程作为内环。在之前的工作中还研究了将退火与去噪分数匹配相结合的想法。针对训练去噪自编码器的噪声提出了不同的退火时间表。然而，这些工作是学习表示以提高分类性能，而不是生成建模。去噪分数匹配方法也可以使用Stein无偏风险估计器的技术从贝叶斯最小二乘的角度推导出来。

结论

本文提出了基于分数的生成建模框架，首先通过分数匹配估计数据密度梯度，然后通过Langevin动力学生成样本。分析了该方法的naïve应用程序所面临的几个挑战，并建议通过训练噪声条件分数网络(NCSN)和使用退火的朗格万动力学采样来解决它们。本文方法不需要对抗性训练，训练过程中不需要MCMC采样，也不需要特殊的模型架构。实验表明，提出的方法可以生成高质量的图像，以前只能由基于最佳似然的模型和GANs生成。在CIFAR-10上实现了最新SOTA的inception分数，以及与SNGANs相当的FID分数。

最后

以上就是还单身火为你收集整理的Generative Modeling by Estimating Gradients of the Data Distribution论文阅读摘要引文基于分数的生成建模/Score-based generative modeling基于分数的生成建模的挑战噪声条件分数网络/NCSN:学习和推理实验相关工作结论的全部内容，希望文章能够帮你解决Generative Modeling by Estimating Gradients of the Data Distribution论文阅读摘要引文基于分数的生成建模/Score-based generative modeling基于分数的生成建模的挑战噪声条件分数网络/NCSN:学习和推理实验相关工作结论所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。