概述
在介绍两种搜索之前，先复习下图的两种存储方式
图的存储
邻接矩阵
设图G(V,E)的顶点为0,1...n-1，那么可以令二维数组G[N][N]的两维分别表示图的顶点编号，即如果G[i][j]为1，说明顶点i和顶点j之间有边；如果G[i][j]为0，则说明顶点i和顶点j之间不存在边，而这个二维数组G则被称为邻接矩阵。另外如果存在边权，则可以令G[i][j]存放边权，对不存在的边可以设边权为0，-1或者一个很大的数。
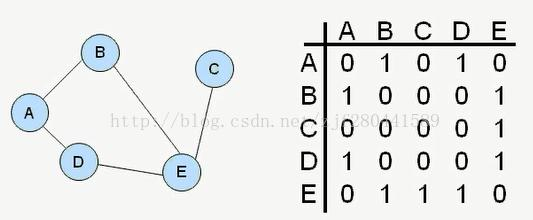
邻接表
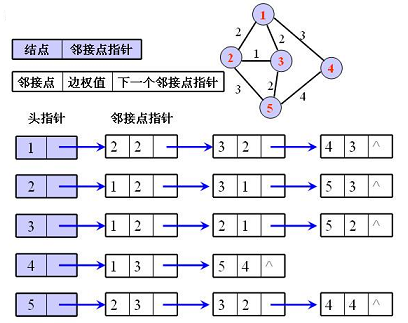
设图G(V,E)的顶点为0,1...n-1，每个顶点都可能有若干条出边，如果把相同的顶点的所有出边放在一个列表中，那么N个顶点就会有N个列表(没有出边，则对应空表)。这N个列表就被称为图G的
邻接表，记为Adj[N]，其中Adj[i]存放顶点i的所有出边组成的列表，如下图就是一个使用链表实现的邻接表：
如果不熟悉链表的同学可以使用vector数组(可变的二维数组)来代替链表，比如使用vector实现的邻接表定义如下：
vector<int> adj[N]adj[1].push_back(3)
深度搜索(DFS)
深度搜索在之前的树的章节也讨论过，其是一种不撞南墙不回头的思想，但是树是连通的，图可能不连通。如下给出深度搜索的伪代码，其适应于邻接表和邻接矩阵：
DFS(u){ //访问顶点u
vis[u]=true; //设置结点u已经被访问过
for(从u出发能到达的所有节点v){
if vis[v]==false //如果v未被访问
DFS(v); //递归访问v
}
}
DFSTrave(G){
for(G的所有顶点u){
if vis[u]==false //如果u未被访问
DFS(u); //访问u所在的连通块
}
}int g[M][M],n; //g=邻接矩阵 n=顶点
bool vis[M]; //记录结点是否被访问过
DFS(int u){ //访问顶点u
vis[u]=true; //设置结点u已经被访问过
for(int v=0;v<n;v++){//从u出发能到达的所有节点v
if(g[u][v] && vis[v]==false) //如果v未被访问(这里无边用0表示)
DFS(v); //递归访问v
}
}
DFSTrave(int g[M][M],int n){
for(int u=0;u<n;u++){
if(vis[u]==false) //如果u未被访问
DFS(u); //访问u所在的连通块
}
}vector<int> adj[M]; //保存邻接结点
int n; // n=顶点
bool vis[M]; //记录结点是否被访问过
void DFS(int u){ //访问顶点u
vis[u]=true; //设置结点u已经被访问过
for(int i=0;i<adj[u].size();i++){//从u出发能到达的所有节点v
int v=adj[u][i];
if(vis[v]==false) //如果v未被访问(这里无边用0表示)
DFS(v); //递归访问v
}
}
void DFSTrave(int g[M][M],int n){
for(int u=0;u<n;u++){
if(vis[u]==false) //如果u未被访问
DFS(u); //访问u所在的连通块
}
}广度搜索(BFS)
广度搜索在之前的树的章节也讨论过，其是一种兔子先吃窝边草的策略。BFS遍历的基本思想是建立一个队列，并把初始顶点加入队列，此后每次都是取出队首顶点进行访问，并把从该顶点可出发可到达的未曾加入过队列(而不是未访问)的顶点全部加入队列，直到队列为空。如下给出广度搜索的伪代码，其适应于邻接表和邻接矩阵：
DFS(u){
queue q; //定义队列q
将结点u加入队列
inq[u]=true; //设置结点u加入过队列
while(q非空){
取出q的队首元素u进行访问
for(从u出发能到达的所有节点v){
if inq[v]==false {//如果v未被访问
将结点v加入队列
inq[v]=true;//设置结点v加入过队列
}
}
}
void BFSTrave(G){
for(G的所有顶点u){
if inq[u]==false //如果u未曾加入过队列
DFS(u); //访问u所在的连通块
}
}
邻接矩阵的实现：
const int M=100;
int g[M][M],n; //g=邻接矩阵 n=顶点
bool inq[M]; //记录结点是否加入过队列
void BFS(int u){ //遍历u所在的连通块
queue<int> q; //定义队列q
q.push(u);//将结点u加入队列
inq[u]=true; //设置结点u加入过队列
while(!q.empty()){
int u=q.front(); //取出q的队首元素u进行访问
q.pop();
for(int v=0;v<n;v++){
if(g[u][v] && inq[v]==false){ //如果v未被访问
q.push(v);//将结点v加入队列
inq[v]=true;//设置结点v加入过队列
}
}
}
}
void BFSTrave(int g[M][M],int n){
for(int u=0;u<n;u++){
if(inq[u]==false) //如果u未被访问
BFS(u); //访问u所在的连通块
}
}
邻接表实现：
vector<int> adj[M]; //保存邻接结点
int n; // n=顶点
bool vis[M]; //记录结点是否被访问过
void BFS(int u){ //遍历u所在的连通块
queue<int> q; //定义队列q
q.push(u);//将结点u加入队列
inq[u]=true; //设置结点u加入过队列
while(!q.empty()){
int u=q.front(); //取出q的队首元素u进行访问
q.pop();
for(int i=0;i<adj[u].size();i++){
int v=adj[u][i];
if(inq[v]==false){ //如果v未被访问
q.push(v);//将结点v加入队列
inq[v]=true;//设置结点v加入过队列
}
}
}
}
void BFSTrave(int g[M][M],int n){
for(int u=0;u<n;u++){
if(inq[u]==false) //如果u未被访问
BFS(u); //访问u所在的连通块
}
}
为了便于讲解，这里的v都是简单的顶点编号。若题目给出的是一个二维坐标，且每一步只能向相邻的方向移动一步(上下左右方向)，此时可以把v修改成其它的类型比如包含坐标x,y以及当前步数step的结构体Node。
struct Node{
int x,y,step;
};int dir[4][2]={{ -1, 0}, {1, 0}, {0, -1}, {0, 1}}; //定义上下左右的方向
for(i=0;i<4;i++){ //遍历相邻的位置
int nx=cur.x+dir[i][0];
int ny=cur.y+dir[i][1];
}最后
以上就是虚幻铅笔为你收集整理的夕拾算法进阶篇：29)深度搜索和广度搜索(图论)的全部内容，希望文章能够帮你解决夕拾算法进阶篇：29)深度搜索和广度搜索(图论)所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复