概述
正态分布：
正态分布的数学期望值或期望值
μ
mu
μ 等于位置参数，决定了分布的位置；其方差
σ
2
sigma^2
σ2 的开平方或标准差
σ
sigma
σ 等于尺度参数，决定了分布的幅度。
常考虑一组数据具有近似于正态分布的概率分布。
若其假设正确，则
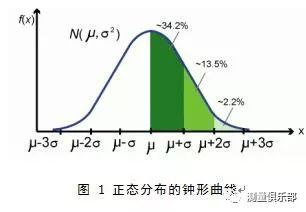
约68.3%数值分布在距离平均值有1个标准差
σ
sigma
σ 之内的范围
约95.4%数值分布在距离平均值有2个标准差
σ
sigma
σ 之内的范围
约99.7%数值分布在距离平均值有3个标准差
σ
sigma
σ 之内的范围
剩下千分之3称之为小概率事件，实际使用通常忽略不计
Normal Distribution 称为正态分布，也称为高斯分布，Truncated Normal Distribution一般翻译为截断正态分布，也有称为截尾正态分布。
截断正态分布是截断分布(Truncated Distribution)的一种，那么截断分布是什么？截断分布是指，限制变量xx 取值范围(scope)的一种分布。例如，限制x取值在0到50之间，即{0<x<50}。因此，根据限制条件的不同，截断分布可以分为：
2.1 限制取值上限，例如，负无穷<x<50
2.2 限制取值下限，例如，0<x<正无穷
2.3 上限下限取值都限制，例如，0<x<50
正态分布则可视为不进行任何截断的截断正态分布，也即自变量的取值为负无穷到正无穷；
最后
以上就是专一哑铃为你收集整理的截断分布与正态分布联系的全部内容，希望文章能够帮你解决截断分布与正态分布联系所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复