在上一篇,我们介绍了时间序列统计建模的几个基本概念:平稳性、自相关和白噪声。时间序列数据的建模是在平稳性的基础上进行的。然而,即使平稳的时间序列依然有潜在无限多的参数(各阶自相关函数),我们需要的是更加简约的(也就是参数个数有限的)平稳时间序列模型,ARIMA模型就是这样一种简约的模型。白噪声是用来建立ARIMA的基本模块。



####AR模型的模拟——stats::arima.simlibrary(tidyverse)library(tsibble)library(cowplot)library(feasts)####ACF函数(自制)gg_acf ACF ACF%>% ggplot(aes(x=lag,y=acf))+ geom_ribbon(aes(ymin=-2/sqrt(T),ymax=2/sqrt(T)), fill=col,alpha=0.4)+ geom_segment(aes(x=lag,xend=lag,y=0,yend=acf),color=col)+ geom_point(shape=21,color=col,fill=col)+ theme_bw() }set.seed(1234)ar1_simar1_sim_tbl%as_tsibble()p1%ggplot(aes(x=index,y=value))+geom_line()+theme_bw()p2%ACF(lag_max=50)%>% gg_acf(col='red',T=100)cowplot::plot_grid(p1,p2,nrow=1)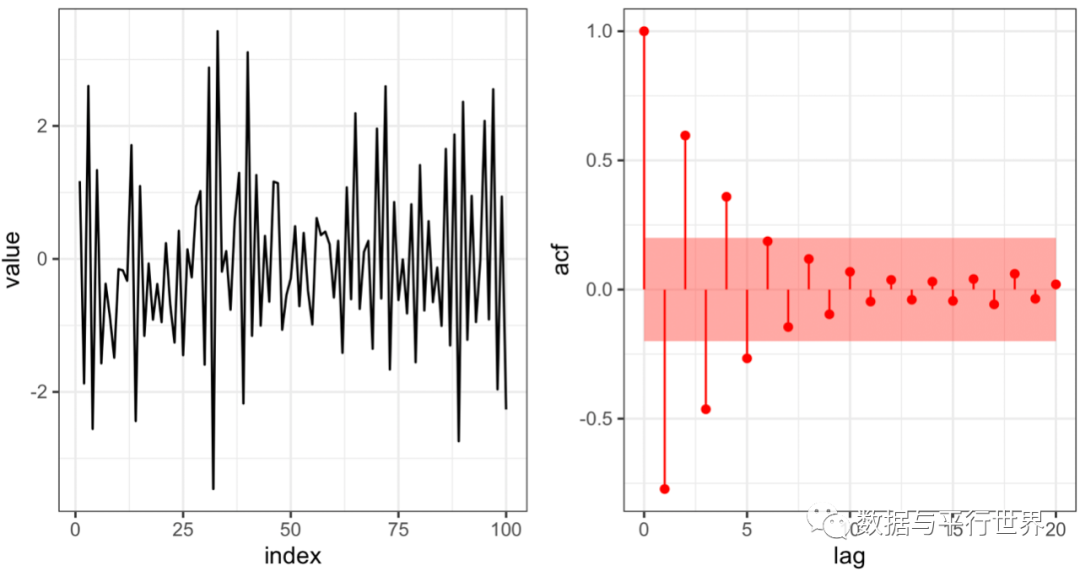 图1
图1

library(plotly) set.seed(1234) p1 for(i in 1:20){ rw p1%add_lines(x=0:(length(rw)-1),y=as.numeric(rw)) }p1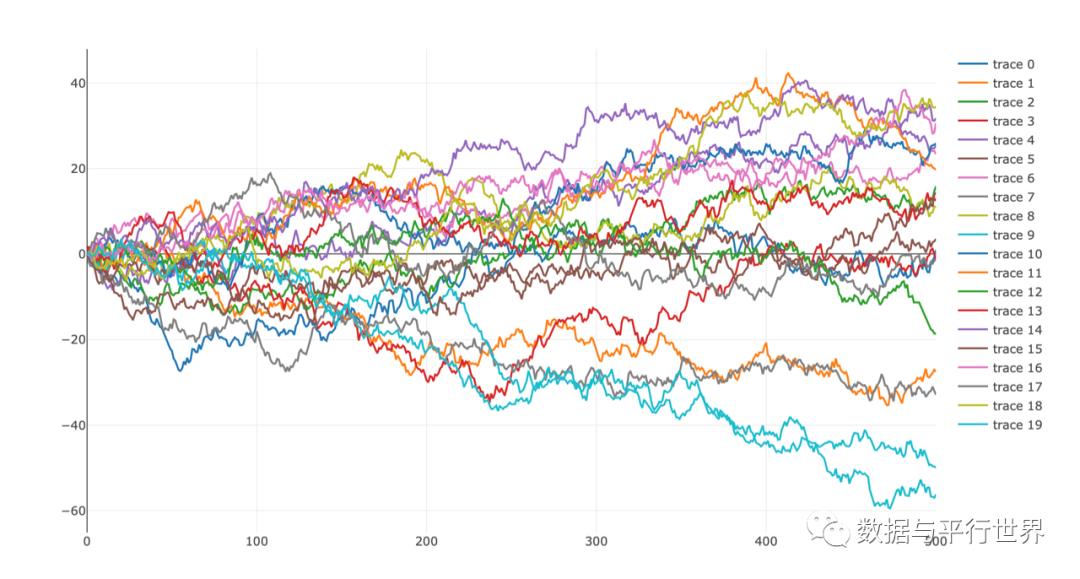 图2
图2


ar2_simar2_sim_tbl%as_tsibble()p1%ggplot(aes(x=index,y=value))+geom_line()+theme_bw()p2%ACF(lag_max=20)%>% gg_acf(col='red',T=100)cowplot::plot_grid(p1,p2,nrow=1)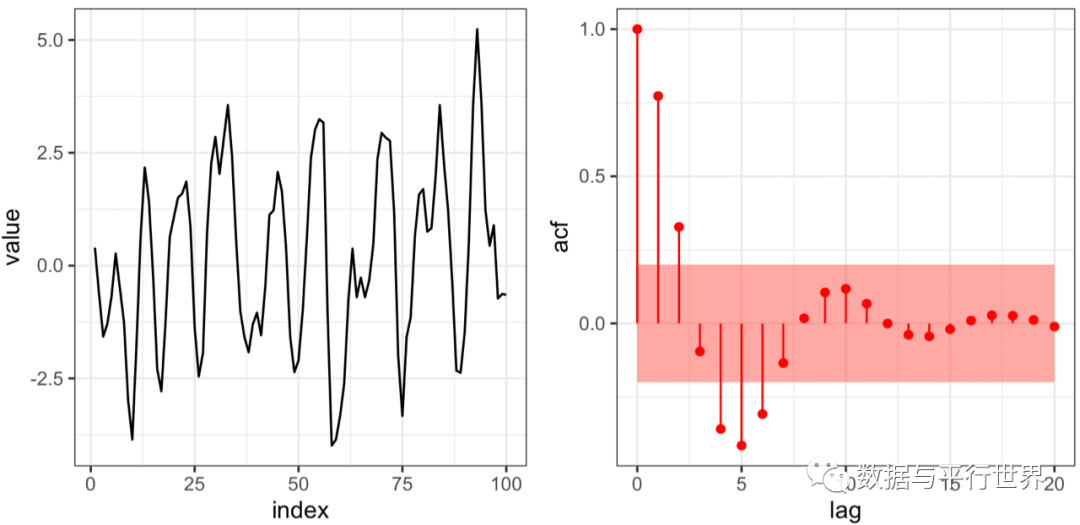 图3
图3

对一个AR(p)模型,滞后为p的PACF应不为零,而对所有j>p的PACF应接近于0。这个性质叫做AR(p)模型的偏自相关函数截尾性。可以利用这一点,帮助确定AR(p)的阶数。
2.4.2 AR模型的建立和筛选
建立AR模型
可以使用极大似然估计或者条件最小二乘估计得到AR模型的参数。估计的数学细节不做讨论。R有多个函数可用于 估计AR模型,特别的,fable包提供了函数AR(),用于估计AR模型。
筛选AR模型
在建立AR(p)模型的时候,我们并不知道真实的阶数p是多少,那么该如何确定一个恰当的阶数p?这需要在模型的复杂度和简洁性之间进行选择。增加滞后项p的个数,可以使残差平方和减少,提升拟合的优度,然而这也会导致过拟合,降低预测的效果。时间序列模型筛选的标准和其他统计模型或机器学习模型的筛选思路是一致的:在保证一定复杂度的前提下,使模型尽可能的简洁。
根据AR(p)模型偏自相关函数的截尾性质,我们可以通过偏自相关图像来判断AR模型的阶数。然而在实际运用中,由于数据并不一定“完美”地符合理论模型,偏自相关图像的截尾性可能表现相当复杂的情况。因此,这一性质可以作为一种经验法则识别AR模型,要筛选出最简洁的模型,信息准则还是更可靠的方法。
信息准则基于似然函数,对模型的参数个数(复杂度)进行惩罚,根据惩罚函数的不同有多种具体的形式。我们常用的信息准则包括赤池信息量AIC和贝叶斯信息准则BIC。
(1)赤池信息量
AIC=-2/T*ln(似然函数)+2*(参数个数)/T
其中,T是样本容量(样本的大小)。AIC的第一项表示了模型的拟合优度(拟合的好坏程度),第二项是罚函数,对过多的参数加以惩罚。
(2)贝叶斯信息准则
将AIC公式第二项中的2替换为ln(T),可以得到贝叶斯信息准则BIC
AIC对每个参数的惩罚为2,BIC对参数的惩罚为ln(T)。所以与AIC相比,在样本容量较大时,BIC倾向于选择一个低阶的AR模型。
例:采用TSstudio包中的数据集Coffee_Prices,这个数据集提供了两种咖啡豆的价格序列。我们选择其中的Robusta(罗布斯塔)的数据建立AR模型。首先,选取原数据集的一个子集并转化为tsibble格式,再对Robusta的价格序列计算差分(考虑到Robusta的价格序列可能并不平稳)。
接下来,通过观察Robusta的价格序列(value)与差分序列(value_diff)的自相关图(图-4),可见value的自相关图呈现缓慢衰减,可以判断是不平稳的,因此选择差分序列进行建模。观察差分序列value_diff的偏自相关图(图-5),一阶滞后的偏自相关是显著不为0的,作为练习,使用AR()函数对p=1到10的情况拟合AR模型。
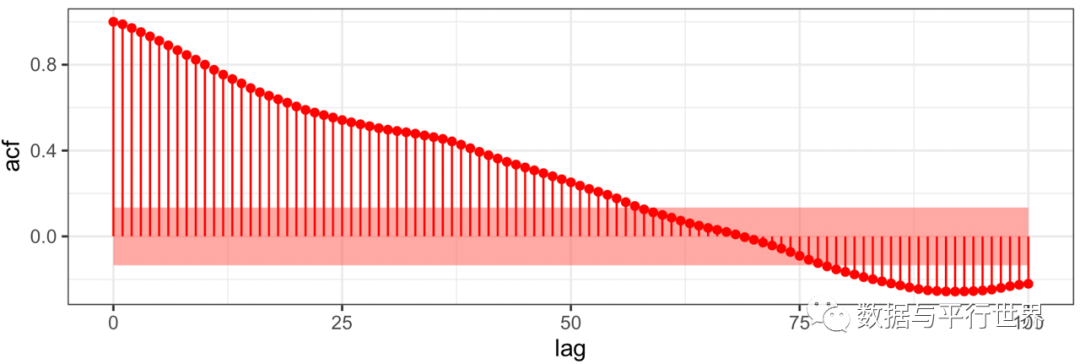 图4
图4
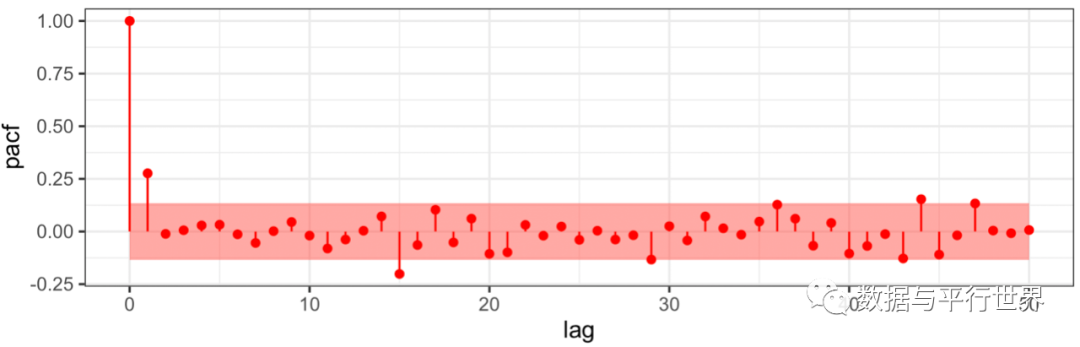 图5
图5
函数AR的用法如下:
AR(formula, ic = c("aicc", "aic", "bic"), ...)其中,formula是进行模型的指定,可以这样来完成:order(p = 0:15, fixed = list())。p参数指定模型的阶数,如果同时指定多个阶数,AR()会根据信息准则的最小值进行筛选(信息准则分别为AIC、AICc和BIC,默认是AIC)。fixed参数用来指定具体的模型系数,如fixed = list(ar1 = 0.3, ar3 = 0)。我们对拟合的模型分别用AIC和BIC准则进行了筛选。代码和运行结果如下:
library(fable)library(TSstudio)coffee_prices% filter(key=="Robusta")%>% mutate(value_diff=difference(value))###价格序列的自相关 coffee_prices%>%ACF(lag_max=100)%>% gg_acf(col='red',T=nrow(coffee_prices))###差分序列的偏自相关coffee_prices%>%select(-value)%>%ACF(type="partial",lag_max=50)%>% gg_acf(col='red',T=nrow(coffee_prices)-1)+ ylab("pacf") ###拟合,分别根据aic和bic选择模型 fit_ar1%model(AR(value_diff~order(1:10),ic="aic"))fit_ar2%model(AR(value_diff~order(1:10),ic="bic"))report(fit_ar1)##Series: value_diff ##Model: AR(1) ##Coefficients:## ar1## 0.2778##sigma^2 estimated as 0.007137##AIC = -16.57 AICc = -16.55 BIC = -13.18report(fit_ar2)##Series: value_diff ##Model: AR(1) ##Coefficients:## ar1## 0.2778##sigma^2 estimated as 0.007137##AIC = -16.57 AICc = -16.55 BIC = -13.18由结果可知,AIC和BIC准则都选择了AR(1)模型。
模型检验
如果拟合的模型是充分的,其残差序列应该是白噪声(即不存在自相关),为了防止模型的不充分性,需要对拟合模型的残差序列进行白噪声检验。使用feasts包的函数gg_tsresiduals()可以对拟合模型的残差序列进行可视化,包括残差的时间序列图,残差序列的自相关图和残差的直方图(以便和正态分布进行比较)(图-6)。使用fable包函数residuals()提取拟合模型的残差序列,并使用函数ljung_box()进行白噪声检验:
###残差的图形gg_tsresiduals(fit_ar1)###残差的白噪声检验fit_resljung_box(fit_res[,3])##lb_stat lb_pvalue ##3.930085e-05 9.949981e-01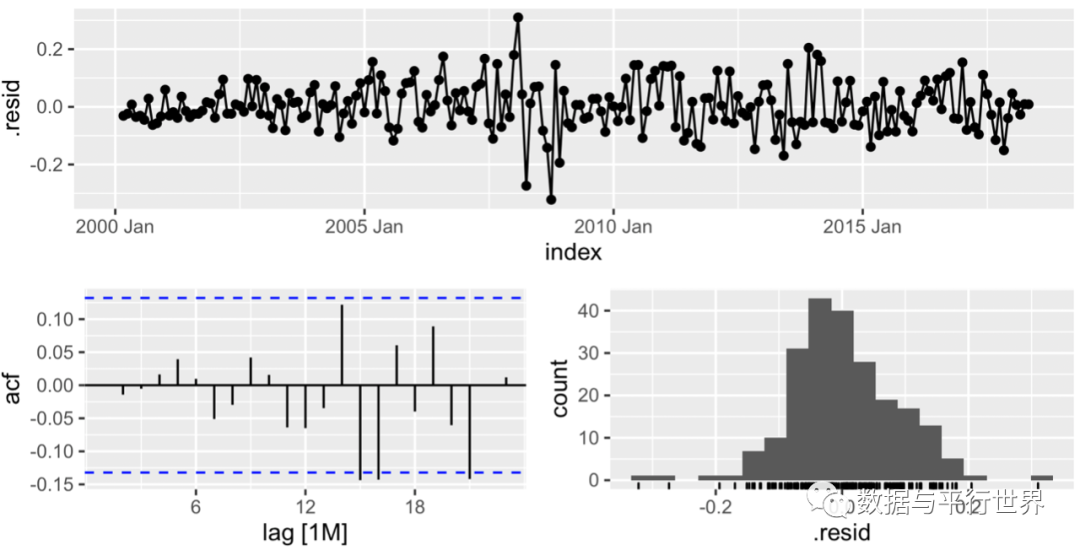 图6
图6
从检验结果可知,拟合模型fit_ar1的残差序列是一个白噪声。
如果残差序列的ACF中显示出显著的相关性,应该考虑对模型加以扩展。
说明:
(1)R中提供了很多时间序列拟合和检验的方法。我们这个系列文章主要采用tidyverst的tsibble包、feasts包和fable包提供的方法。需要注意的是,tidyverst的主要目标是时间序列预测,而且还在开发之中,功能还不够全面。很多其他R工具或许会给出更全面的结果,比如说作为tidyverst前身forecast包。然而,forecast并不支持tidyverse语法。
(2)关于AR模型的检验。对于拟合的AR(k)模型,除了检验残差序列符合白噪声之外,还应该检验模型系数的显著性,如果某个系数不显著,可以在拟合模型中去掉该系数对应的项,这样可以简化拟合模型。具体做法可以参考[2]
(3)这篇公式有点多,没找到更好的展示方法,只好做了截图。阅读体验不太好,抱歉了各位。
参考:
[1]、汉密尔顿,《时间序列分析》,中国人民大学出版社,2015.
[2]、蔡瑞胸,《金融数据分析导论》,机械工业出版社,2016.
最后
以上就是愤怒水杯最近收集整理的关于时间序列的截尾和拖尾_R时间序列分析(8)ARIMA(上)的全部内容,更多相关时间序列内容请搜索靠谱客的其他文章。








发表评论 取消回复