二叉搜索树的广度优先遍历

在上一节中，我们学习了二叉树的而前序遍历，中序遍历，以及后续遍历。但是我们发现，上述三种遍历方式都使用到了递归，因此无论哪种遍历都是一直往深处遍历到不能遍历为止。那么，有没有什么方法能够将每一层的节点遍历完然后在遍历下一层的节点呢？能够解决这种问题呢，因此，接下来我们就要开始讨论二叉树的广度优先遍历。

对于广度遍历，我们需要额外引进一个辅助工具，那就是我们熟悉的数据结构中的一种：队列。

让我们先看一下具体是怎么操作的吧。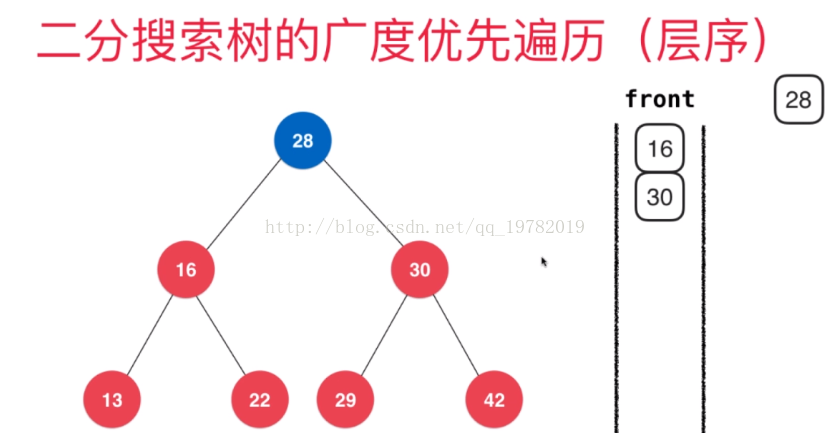

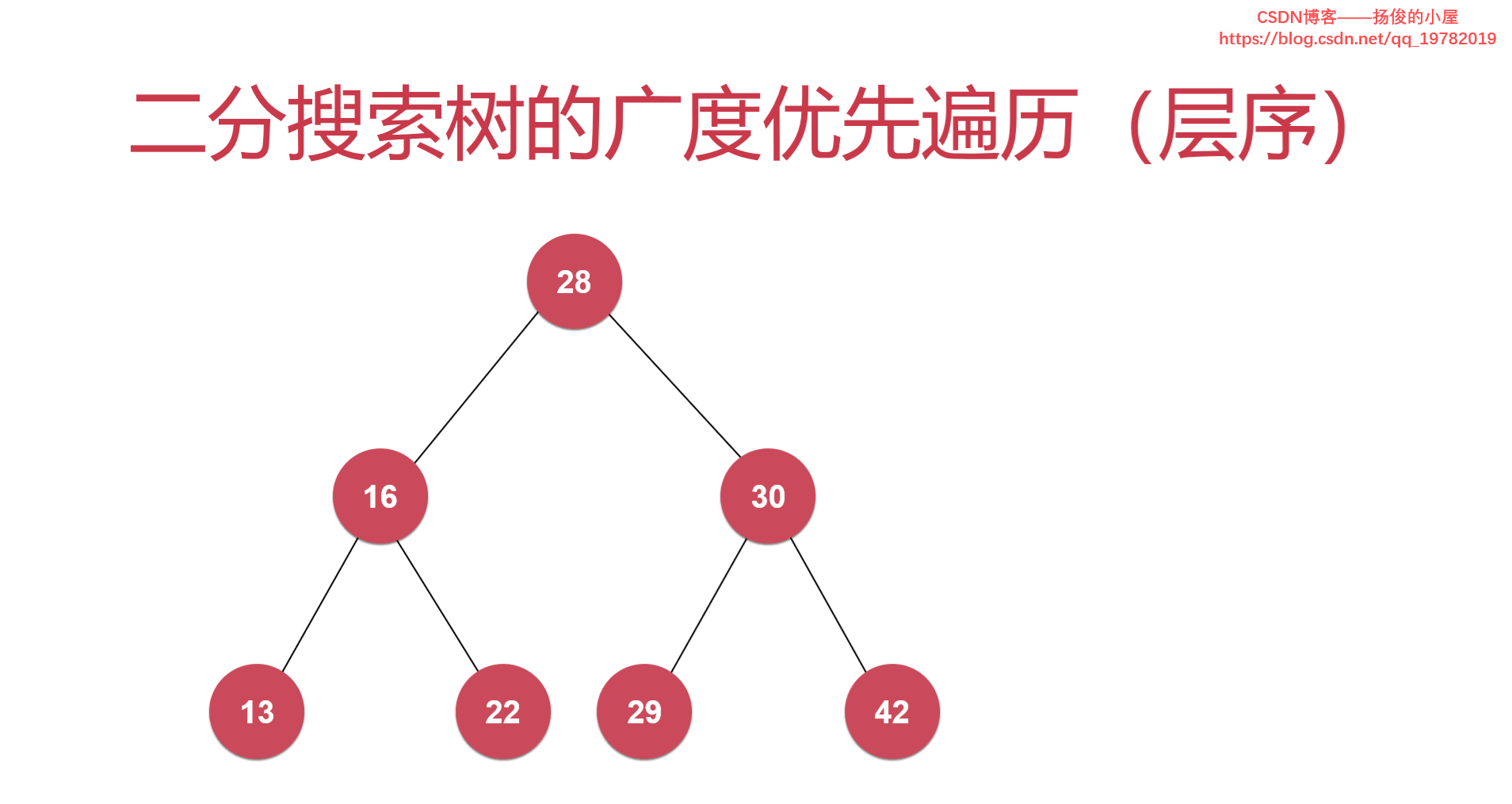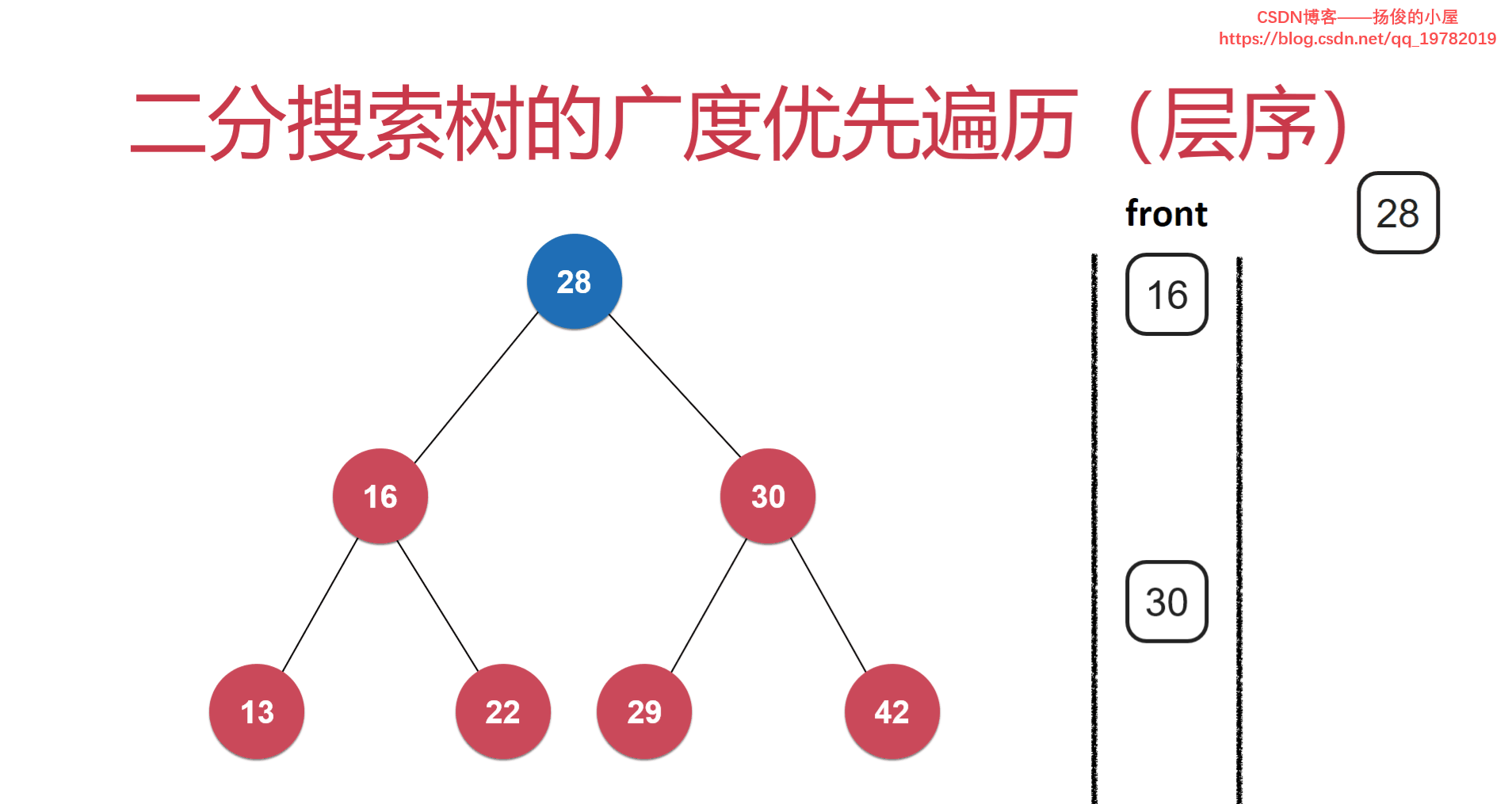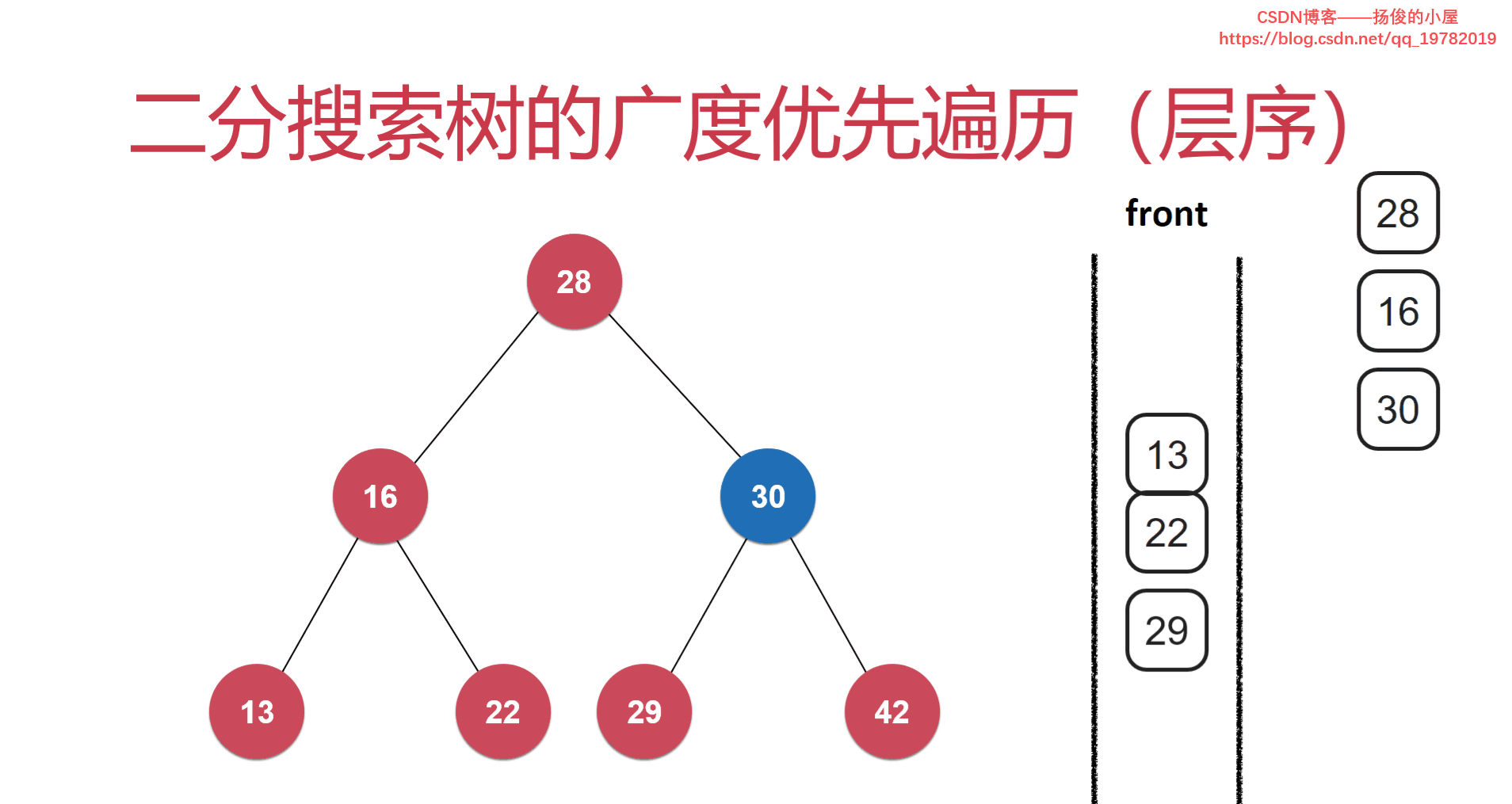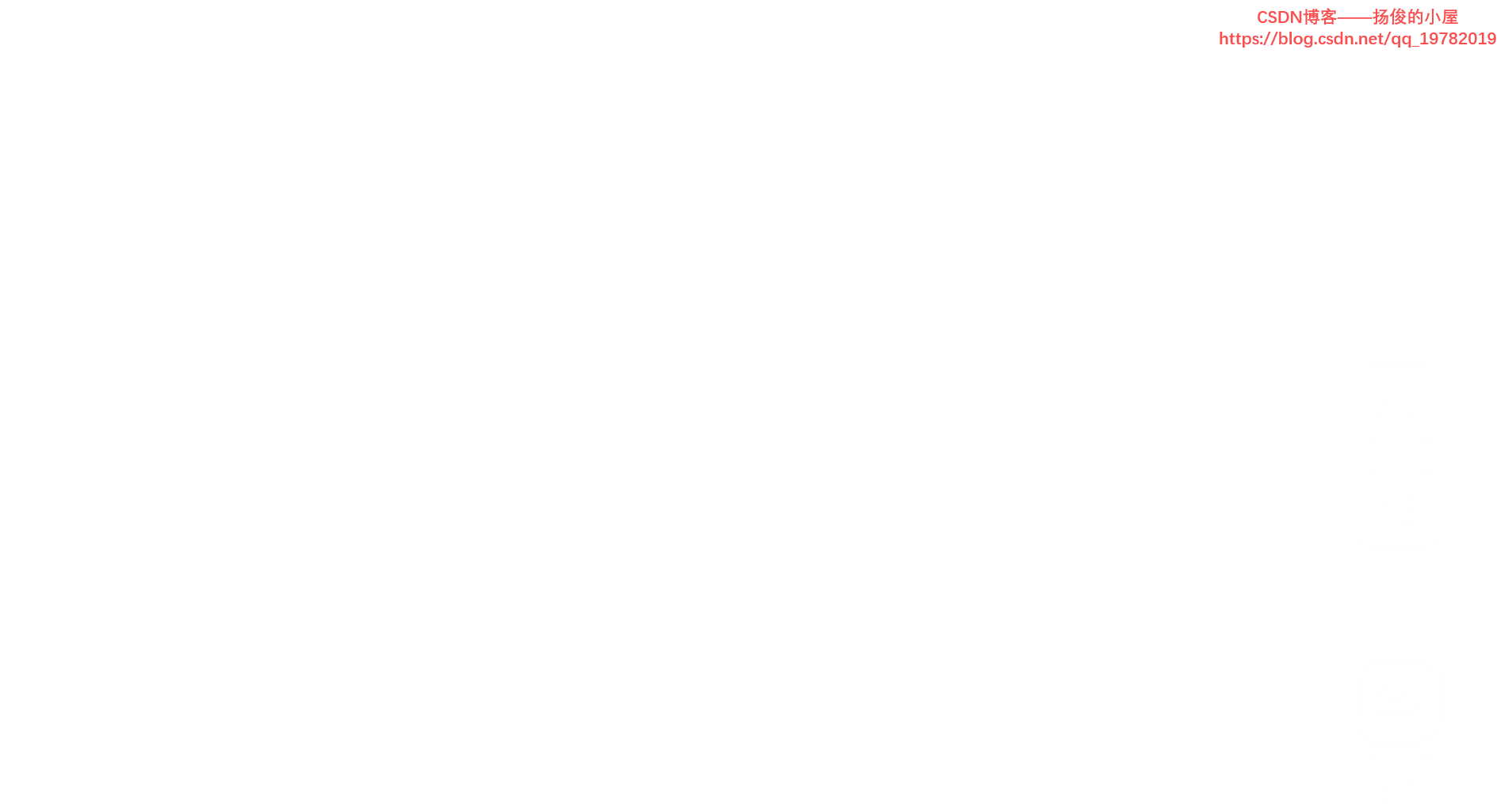
首先，我们new一个队列出来，队列的特点想必大家都已经了解了：先进先出。所以，我们可以先把整棵树的根节点第一个加入队列。然后通过队列的front方法把队列的首元素的地址返回出来（此处的根节点地址）并赋值给一个专门记录需要被遍历的节点的地址node，然后在去访问该节点（node）的元素。当node指向的节点被访问后，我们在去看一下node节点有没有孩子节点啊？如果有的话，就把他的左右孩子节点都给加入队列，这样位于此处（此时队列的首元素）就能安心的离开这个队列了。如果每一个节点排到队列的队首被访问后，都把自己的孩子节点全部加入队列后，在安心的离开队列的话，这样遍历的顺序就是按照层序遍历来的。

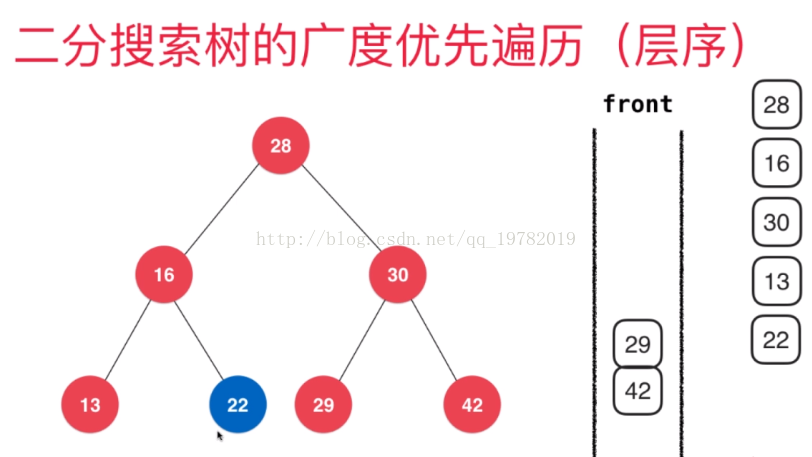
上图中，我们发现出队的顺序都是按照层序遍历出队的。28节点带了他的两个子节点16和30入队，16带了他的两个子节点13,22入队,30带了他的两个子节点29,42.......。依此循环，可以保证二叉树是一层一层被遍历的。

以下是相应程序遍历的部分代码：

void leverorder(){
        queue<node*> duilie;
        if(root!=NULL){//必须存在二叉树才能够进行层序遍历
            duilie.push(root);
            while (!duilie.empty()){
                    node*node=duilie.front();
                    cout<<node->key<<' ';
                    if(node->left!=NULL){
                        duilie.push(node->left);
                    }
                    if(node->right!=NULL){
                        duilie.push(node->right);
                    }
                    duilie.pop();


            }
        }
    }

让我们来看一下结果：

a.insert(3,4);
    a.insert(2,4);
    a.insert(9,4);
    a.insert(1,4);
    a.insert(5,4);
    a.inorder();
    cout<<endl;
    a.leverorder();

输出结果如下图所示：

1 2 3 5 9
3 2 9 1 5

如果您想访问完整的二叉树源代码，请点击此处。

最后

以上就是不安短靴为你收集整理的二叉搜索树的广度优先遍历的全部内容，希望文章能够帮你解决二叉搜索树的广度优先遍历所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。