跳台阶及其一系列的动态规划问题

90 阅读 0 评论 60 点赞

我是靠谱客的博主多情皮皮虾，最近开发中收集的这篇文章主要介绍跳台阶及其一系列的动态规划问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目1：变态跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

解法1：(逆向求解）

跳n阶，可以从n-1阶，n-2阶, n-3阶…0阶的基础上跳一次到达n阶，就是将n-1阶到0阶的各个跳法并求和。

int jumpFloorII(int number)
	{
		int sum = 0;
		if (number <= 1)
		{
			return 1;
		}
		else
		{
			while (number--)
			{
				sum += jumpFloorII(number);
			}
			return sum;
		}
	}

解法2：(顺向求解)

跳1阶，剩下n-1阶, 剩下跳法是f(n-1)
跳2阶，剩下n-2阶，剩下跳法是f(n-2)
…
跳n阶，剩下n-n阶，剩下跳法是f(0)

f(n) = f(n - 1) + f(n - 2) + …f(0)
f(n - 1) = f(n - 2) + f(n - 3) + …f(0)
…
动态方程：f(n) = 2 * f(n - 1);

int jumpFloorII(int number)
	{
		int fn = 1,fn_1;
		if (number <= 0)
		{
			return 0;
		}
		for (int i = 2; i <= number; i++)
		{
			fn_1 = fn;
			fn = 2 * fn_1;
		}
		return fn;
	}

解法3:(在解法2的基础之上用数学归纳法列举一下）

初值:f(1) = 1;
f(2) = 2* f(1) = 2
f(3) = 2* f(2) = 4
f(4) = 2* f(3) = 8
…
终极表达式:f(n) = 2^(n-1)

int jumpFloorII(int number)
{
	return 1 << (number - 1);
}

题目2：跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果)。这是牛客网的题目要求，这里我做以调整，有number阶台阶，青蛙最多可以跳max_step阶，其他不变。

有题目1的引导：我们可以直接写出动态转移方程：
f(n) = f(n - 1) +f(n - 2) +f(n - 3) …+f(n -max_step)
因为青蛙的max_step是不确定的，所以这个题就不能使用逆向求解来解决，不能使用归纳法取列举各个状态的情况。

int jumpFloor(int number,int max_step)//在原题目的基础上加了一个参数max_step---表示青蛙跳台阶的最大步数
{
	int i, sum = 0;
	if (number <= 1)
	{
		return 1;
	}
	for (i = max_step; i > 0; i--)
	{
		number--;
		if (number < 0)
		{
			break;
		}
		sum += jumpFloor(number);
	}
	return sum;
}

题目3：矩形覆盖

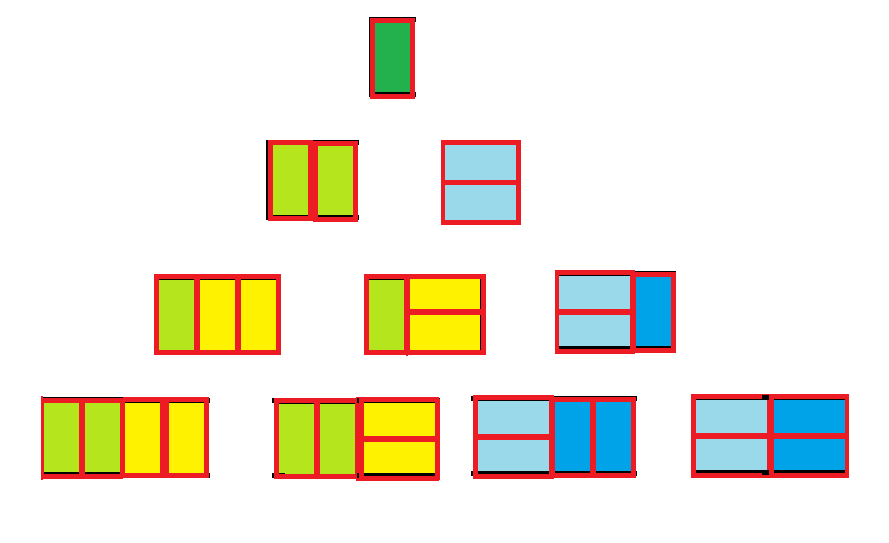
我们可以用2* 1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2* 1的小矩形无重叠地覆盖一个2* n的大矩形，总共有多少种方法？

根据图片可以看出：
n = 1 的时候，只能横着覆盖，一种
n = 2 的时候，可以横着和竖着覆盖，两种
n = 3 的时候
第三级横着覆盖，用了一级，剩下 n = 2，有两种覆盖方法
第三季竖着覆盖，用了两级，剩下 n = 1，有一种覆盖方法
总共有 3 种
n = 4 的时候
第 4 级横着覆盖，用了一级，剩下 n = 3，有三种覆盖方法
第 4 级竖着覆盖，用了两级，剩下 n = 2，有两种覆盖方法
总共有 5 种方法
n = n 的时候
第 n 级横着覆盖，用了一级，剩下 n = n - 1，所以关注第 n - 1 种有几种覆盖方法
第 n 级竖着覆盖，用了两级，剩下 n = n - 2，所以关注第 n - 2 种有几种覆盖方法
总和为n-1和n-2两种情况的总和
所以可以得出动态转移方程：f(n) = f(n - 1) + f(n- 2)
这又是一个斐波那契数列的变种题。。。。

class Solution {
public:
	int rectCover(int number)
	{
		int fn = 1, fn_1 = 1, fn_2 = 1;
		if (number <= 0)
		{
			return 0;
		}
		if (number == 1)
		{
			return 1;
		}
		for (int i = 2; i <= number; i++)
		{
			fn_2 = fn_1;
			fn_1 = fn;
			fn = fn_1 + fn_2;
		}
		return fn;
	}
};