数据结构 | 后缀表达式【深入剖析堆栈原理】❓初见：什么是后缀表达式????磨砺：怎样将中缀表达式转换为后缀表达式【⭐⭐⭐⭐⭐】✒闭隐：如何对后缀表达式进行求值？【⭐⭐⭐】????观镜：结果测试????开战：实战演练【LeetCode习题深入】????归思：总结与提炼

84 阅读 0 评论 56 点赞

我是靠谱客的博主标致草莓，最近开发中收集的这篇文章主要介绍数据结构 | 后缀表达式【深入剖析堆栈原理】❓初见：什么是后缀表达式????磨砺：怎样将中缀表达式转换为后缀表达式【⭐⭐⭐⭐⭐】✒闭隐：如何对后缀表达式进行求值？【⭐⭐⭐】????观镜：结果测试????开战：实战演练【LeetCode习题深入】????归思：总结与提炼，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

在这里插入图片描述

Hello，大家好，国庆的第二天，带来的是数据结构中堆栈部分的后缀表达式，这也是一块有关栈的应用方面困扰了众多同学的一个大难题，今天就让我们一起解决这个难题????

堆栈应用之后缀表达式

❓初见：什么是后缀表达式
- 后缀表达式的优势
????磨砺：怎样将中缀表达式转换为后缀表达式【⭐⭐⭐⭐⭐】
- ????熟悉规则【重点基础掌握】
- ????层层剖析【堆栈原理展示】
- ????手撕代码【不信你看不懂】
✒闭隐：如何对后缀表达式进行求值？【⭐⭐⭐】
- ????运算规则
- ????关键代码讲解
????观镜：结果测试
- ????测试结果展示
- ????整体代码展示
????开战：实战演练【LeetCode习题深入】
- ????题目描述
- ????思路分析
- ????动画展示
- ????整体代码展示
- ????重点讲解
????归思：总结与提炼

❓初见：什么是后缀表达式

后缀表达式也称为逆波兰表达式，也就是将算术运算符放在操作数的后面

例如【1 + 2 * 3】的后缀表达式形式变为【1 2 3 * +】，前面的那个叫做中缀表达式，也就是我们最常用的，遵循的规则是“先乘除，后加减”；
那有些小伙伴就很疑惑，为什么要这么去做呢，好好地用我门正常的计算形式去运算不就好了，下面我们就来讲讲后缀表达式

后缀表达式的优势

对于后缀表达式，它十分地有用，因为其可以把复杂的表达式转化为依靠简单操作得到的计算结果的表达式。就我们上面这个表达式来看，是非常简单的，但如果换一个复杂一些的呢，你能够在短期时间内把它计算出来吗????

可以看出，对于这个中缀表达式，是比较复杂的，但是我们利用后缀表达式去简化，看起来就没有这么复杂了，利用这个表达式与堆栈的先进后出【FILO】原理，就可以达到事半而功倍的效果

????磨砺：怎样将中缀表达式转换为后缀表达式【⭐⭐⭐⭐⭐】

相信这部分是大家最难过的一道坎，让我们来一探究竟????

????熟悉规则【重点基础掌握】

首先，最重要的一点是你必须知道转换的规则

????法则一：如果遇到一个运算符op以及左括号“（”，此时栈如果为空，则直接将其进栈
????法则二：若是遇到了操作数num，就将其直接输出
????法则三：如果栈不为空，则只有当op的优先级高于栈顶运算符优先级时才将其进栈，否则将栈顶op弹出
????法则四：若当前op进栈时发现栈中有与之相同op，则出栈其一，再加当前op压入栈中
????法则五：若遇到右括号，则开始弹出栈字符，直到左括号为止
????法则六：只要当遇到右括号“）”时，才从栈中弹出左括号“（”，否则一直遍历

以上法则是我们要了解后缀表达式转换的基本，你必须将其记牢

????层层剖析【堆栈原理展示】

有了固定的发展，接下来就是具体的案例和分析

我们以此表达式为例进行讲解【5 + 8*2 + ( 3 * 9 + 6 )*4】

Part1

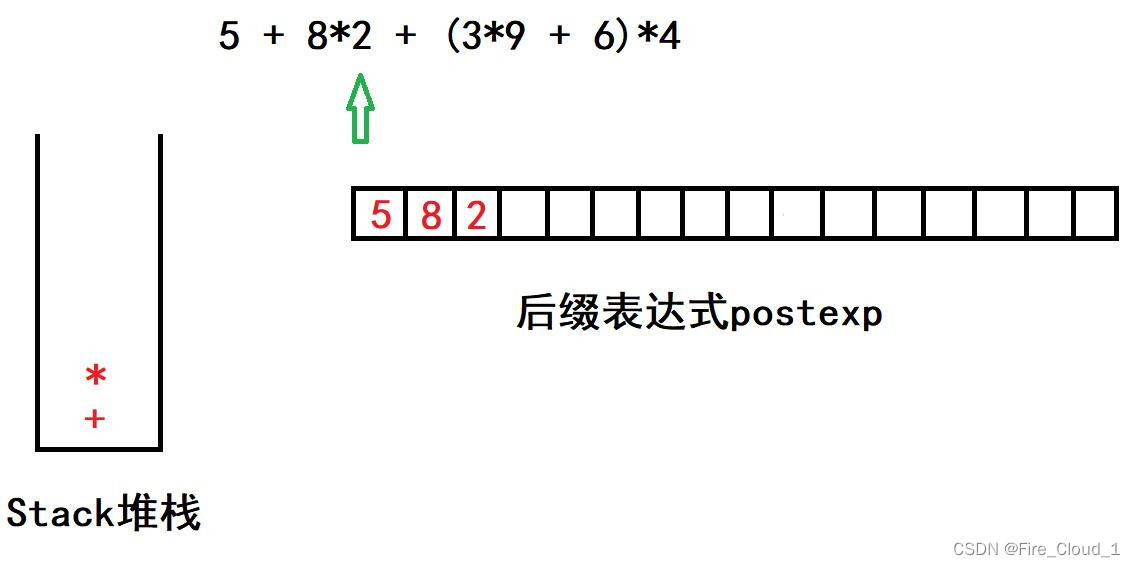
首先是5，根据法则二，直接放入表达式
然后是操作符【+】，根据法则一，栈为空，直接入栈
接着是8，同理，直接放入表达式
其次是操作符【*】，因优先级高于【+】，故直接入栈
最后又碰到一个2，同理，直接放入表达式

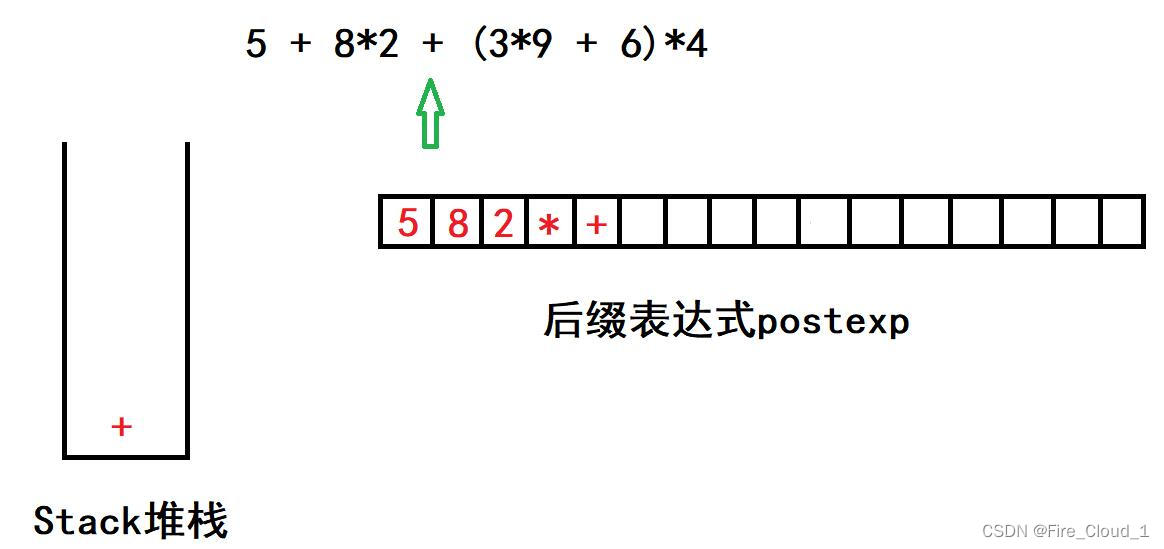
Part2
【5 + 8*2 + ( 3 * 9 + 6 )*4】

读到【+】，这时要注意，引起优先级低于【*】，所以乘号出栈，放入表达式，但此时遍历到的操作符op与栈中的【+】一致，故栈中的【+】也因放入表达式，接着将遍历到的【+】入栈

Part3
【5 + 8*2 + ( 3 * 9 + 6 )*4】

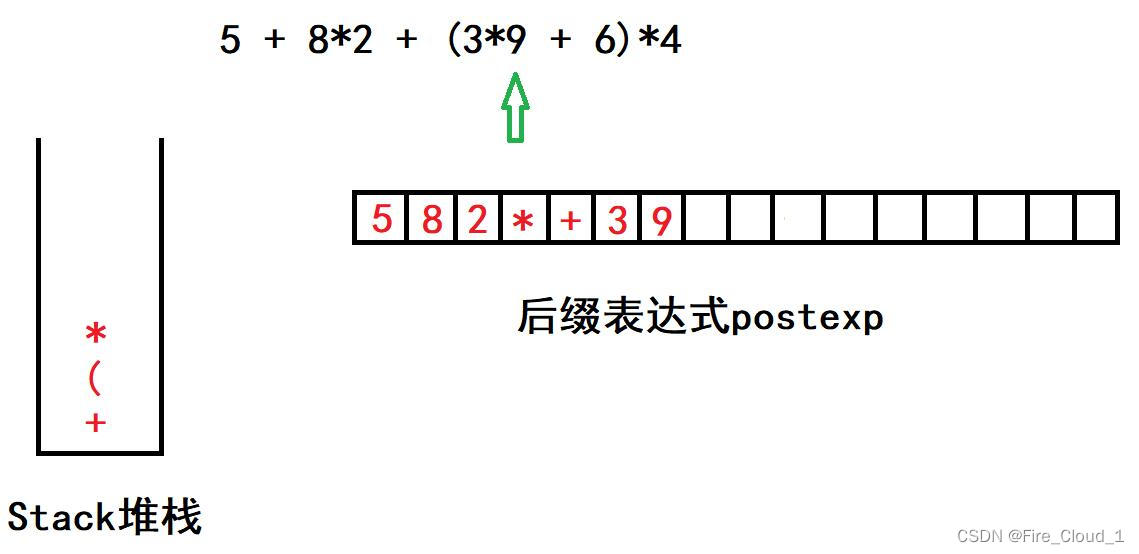
首先读到左括号【(】，这代表一个子表达式的开始，因其优先级最高，故直接入栈
然后是3，根据法则二，直接放入表达式
接着遇到【*】，此时要注意，根据法则六，因为还没有碰到右括号【)】，说明子表达式还没结束，故直接入栈
最后是9，同理，放入表达式

Part4
【5 + 8*2 + ( 3 * 9 + 6 )*4】

首先我们遇到【+】，这是看到栈顶op为【*】，比其低，根据法则三，弹出栈顶元素，并将当前op入栈
然后是6，根据法则二，直接放入表达式
最后读到【)】，表示子表达式结束，开始逐个弹出栈顶元素，直到左括号【(】弹出后结束（括号均不放入表达式）

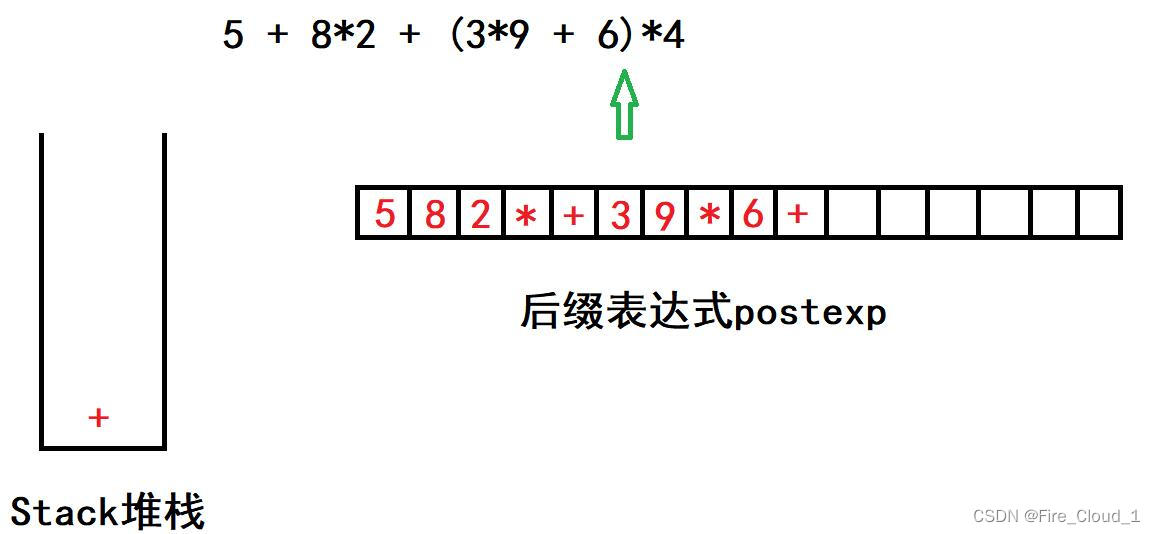
在这里插入图片描述

Part5
【5 + 8*2 + ( 3 * 9 + 6 )*4】

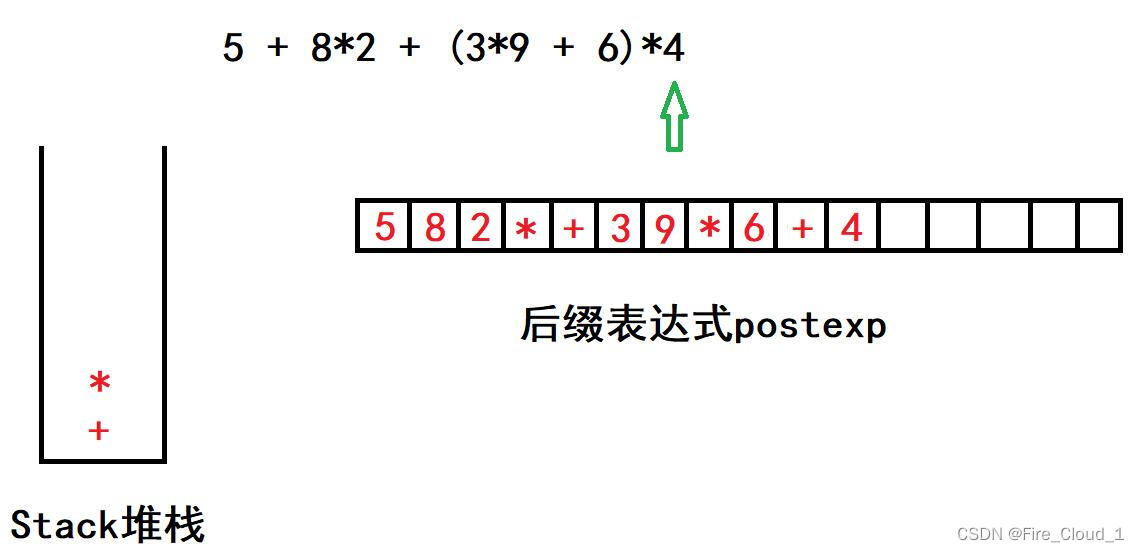
碰到【*】，因其优先级高于栈中的【+】，故直接入栈
然后是4，根据法则二，直接放入表达式

Part6
【5 + 8*2 + ( 3 * 9 + 6 )*4】

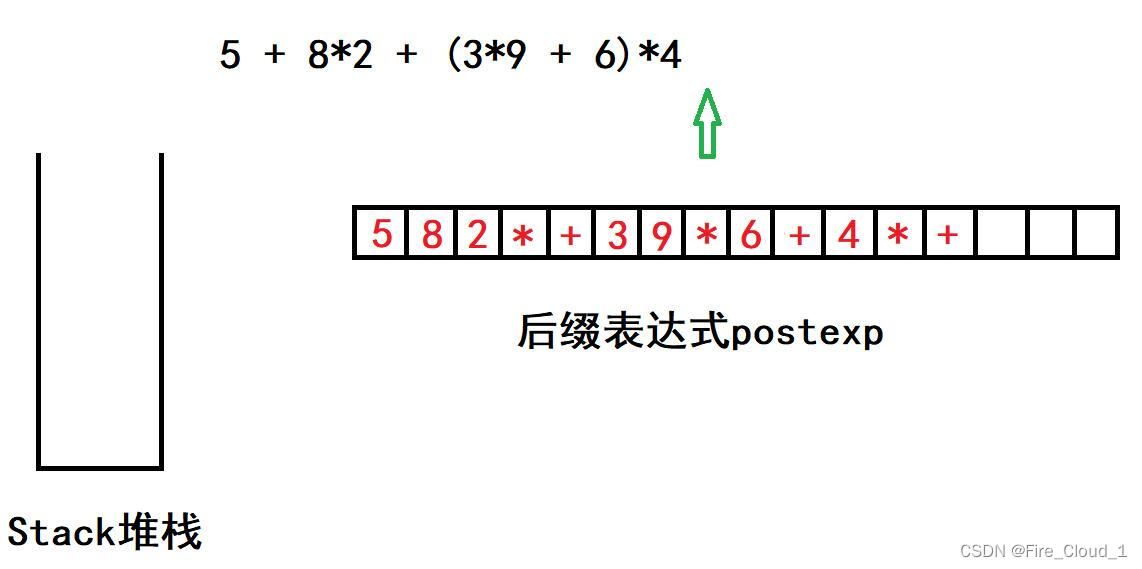
最后遍历到末尾，栈中还有两个操作符op，直接弹出即可（不放入表示式）

最后的postexp即为转换后的后缀表达式【582*+39*6+4】

????手撕代码【不信你看不懂】

了解了堆栈的基本原理后，接下来就是代码环节，也是可视化计算的重要一趴

void trans(char* exp, char postexp[])	//将算术表达式exp转换成后缀表达式postexp
{
	char e;
	SqStack* Optr;						//定义运算符栈
	InitStack(Optr);					//初始化运算符栈
	int i = 0;							//i作为postexp的下标
	while (*exp != '')					//exp表达式未扫描完时循环
	{
		switch (*exp)
		{
		case '(':						//判定为左括号
			Push(Optr, '(');				//左括号进栈
			exp++;						//继续扫描其他字符
			break;
		case ')':						//判定为右括号
			Pop(Optr, e);				//出栈元素e
			while (e != '(')				//不为'('时循环
			{
				postexp[i++] = e;			//将e存放到postexp中
				Pop(Optr, e);			//继续出栈元素e
			}
			exp++;						//继续扫描其他字符
			break;
		case '+':						//判定为加或减号
		case '-':
			while (!StackEmpty(Optr))	//栈不空循环
			{
				GetTop(Optr, e);			//取栈顶元素e
				if (e != '(')				//e不是'('
				{
					postexp[i++] = e;		//将e存放到postexp中
					Pop(Optr, e);		//出栈元素e
				}
				else					//e是'(时退出循环
					break;
			}
			Push(Optr, *exp);			//将'+'或'-'进栈
			exp++;						//继续扫描其他字符
			break;
		case '*':						//判定为'*'或'/'号
		case '/':
			while (!StackEmpty(Optr))	//栈不空循环
			{
				GetTop(Optr, e);			//取栈顶元素e
				if (e == '*' || e == '/')	//将栈顶'*'或'/'运算符出栈并存放到postexp中
				{
					postexp[i++] = e;		//将e存放到postexp中
					Pop(Optr, e);		//出栈元素e
				}
				else					//e为非'*'或'/'运算符时退出循环
					break;
			}
			Push(Optr, *exp);			//将'*'或'/'进栈
			exp++;						//继续扫描其他字符
			break;
		default:				//处理数字字符
			while (*exp >= '0' && *exp <= '9') //判定为数字
			{
				postexp[i++] = *exp;
				exp++;
			}
			postexp[i++] = ' ';	//用#标识一个数值串结束
		}
	}
	while (!StackEmpty(Optr))	//此时exp扫描完毕,栈不空时循环
	{
		Pop(Optr, e);			//出栈元素e
		postexp[i++] = e;			//将e存放到postexp中
	}
	postexp[i] = '';			//给postexp表达式添加结束标识
	DestroyStack(Optr);			//销毁栈		
}

看完这串代码，不用猜，我知道你已经已经想点下浏览器中这个网页的【×】了。但是何妨不听我讲完再说

这里我们需要用到顺序的结构实现原理SqStack，代码在最后给出，这里就展示转换的算法部分
整体浏览，这串代码处于一个while循环之中，也就是对给出的字符串进行的一个遍历，【!= ‘’】在C语言中表示还没到字符串结尾
在大层的while循环之下是一个switch()分支判断，判断的就是当前所遍历的exp，在英文中是expression【表达式】，上面讲到的postexp就是postexpression【后缀表达式】，我们的目的就是要去exp中遍历每一个字符，然后将符合条件的字符按照后缀表达式的法则以及堆栈的原理一个个地放入postexp中，然后我们来分别说说每个case的判断
首先是左括号【(】，这个直接进栈即可，exp++表示将遍历下一个字符，break表示的跳出当前的case分支，若是不写这一句，则程序会一直往下走，直到下一个break才会跳出

case '(':						//判定为左括号
	Push(Optr, '(');				//左括号进栈
	exp++;						//继续扫描其他字符
	break;

接着是右括号【)】，上面说过了，若是碰到右括号，则开始出栈栈顶元素，知道栈顶元素为左括号【(】时，while体中的语句就是将当前出栈的元素放入postexp后缀表达式中，i++表示为下一个位置留出位置，然后Pop出栈即可，循环结束后继续扫描下一个字符

case ')':						//判定为右括号
	Pop(Optr, e);				//出栈元素e
	while (e != '(')				//不为'('时循环
	{
		postexp[i++] = e;			//将e存放到postexp中
		Pop(Optr, e);			//继续出栈元素e
	}
	exp++;						//继续扫描其他字符
	break;

然后是【+】【-】，它们的循环条件是栈不为空，首先去获取栈顶元素，若获取的元素不为左括号【(】，则表示子表达式没结束，不停地将栈顶元素放入postexp中，然后出栈。若是碰到了左括号【(】，则跳出当前循环，循环后将当前的【+】【-】入栈，继续扫描下一个字符

case '+':						//判定为加或减号
case '-':
	while (!StackEmpty(Optr))	//栈不空循环
	{
		GetTop(Optr, e);			//取栈顶元素e
		if (e != '(')				//e不是'('
		{
			postexp[i++] = e;		//将e存放到postexp中
			Pop(Optr, e);		//出栈元素e
		}
		else					//e是'(时退出循环
			break;
	}
	Push(Optr, *exp);			//将'+'或'-'进栈
	exp++;						//继续扫描其他字符
	break;

其次就是【*】【/】，同样，也是在栈不空时循环，获取到栈顶元素，若是碰到相同的乘号或除号，则将它们放入postexp中，若是没有，则跳出循环，直接将它们放入栈中即可

case '*':						//判定为'*'或'/'号
case '/':
	while (!StackEmpty(Optr))	//栈不空循环
	{
		GetTop(Optr, e);			//取栈顶元素e
		if (e == '*' || e == '/')	//将栈顶'*'或'/'运算符出栈并存放到postexp中
		{
			postexp[i++] = e;		//将e存放到postexp中
			Pop(Optr, e);		//出栈元素e
		}
		else					//e为非'*'或'/'运算符时退出循环
			break;
	}
	Push(Optr, *exp);			//将'*'或'/'进栈
	exp++;						//继续扫描其他字符
	break;

最后就是另外的数字情况的判断，若为数字字符，直接将其放入postexp中即可，然后在每个数字后加一个空格来进行标识

default:				//处理数字字符
	while (*exp >= '0' && *exp <= '9') //判定为数字
	{
		postexp[i++] = *exp;
		exp++;
	}
	postexp[i++] = ' ';	//用空格标识一个数值串结束

最后面的这段就是处理最后栈中还剩余的元素，将其依次出栈放入postexp即可，直到栈为空为止，最后别忘了postexp也是一个字符串，既然是字符串最后就要手动加上’’，就是尾插法最后要的r - >next = NULL是一个道理

while (!StackEmpty(Optr))	//此时exp扫描完毕,栈不空时循环
{
	Pop(Optr, e);			//出栈元素e
	postexp[i++] = e;			//将e存放到postexp中
}
postexp[i] = '';			//给postexp表达式添加结束标识
DestroyStack(Optr);			//销毁栈

看完了上面的细致讲解，难道你还想退出吗，不想的话就继续跟着我来吧????

✒闭隐：如何对后缀表达式进行求值？【⭐⭐⭐】

将中缀表达式转换为后缀表达式后，只是完成了我们的第一步，也就是有了一个模型了，接下去就要将其细心雕刻直至完美????

对后缀表达式的求值并不是很难，但是也需要涉及到堆栈FILO的原理，这需要你对Stack非常得熟悉
这里的顺序栈数据结构体的数据类型要记得换一下，不可以用char了，前面我们是在遍历字符，所以用char，但是这里是要去求值，但是数字可能会是小数，所以最好声明成double类型，这个不难，只需要改一下各个数据类型即可

????运算规则

首先一样，我们要了解一下其运算规则

后缀表达式求值的算法是遍历后缀表达式，如果遇到运算数，那么运算数入栈
如果遇到运算符，那么弹出栈里面两个元素，先弹出的是右运算数，后弹出的是左运算数，计算运算结果，然后将结果入栈。最后遍历到后缀表达式末尾，当结果只有一个元素时，就是答案

double compvalue(char* postexp)	//计算后缀表达式的值
{
	double d, a, b, c, e;
	SqStack1* Opnd;				//定义操作数栈
	InitStack1(Opnd);			//初始化操作数栈
	while (*postexp != '')		//postexp字符串未扫描完时循环
	{
		switch (*postexp)
		{
		case '+':				//判定为'+'号
			Pop1(Opnd, a);		//出栈元素a
			Pop1(Opnd, b);		//出栈元素b
			c = b + a;				//计算c
			Push1(Opnd, c);		//将计算结果c进栈
			break;
		case '-':				//判定为'-'号
			Pop1(Opnd, a);		//出栈元素a
			Pop1(Opnd, b);		//出栈元素b
			c = b - a;				//计算c
			Push1(Opnd, c);		//将计算结果c进栈
			break;
		case '*':				//判定为'*'号
			Pop1(Opnd, a);		//出栈元素a
			Pop1(Opnd, b);		//出栈元素b
			c = b * a;				//计算c
			Push1(Opnd, c);		//将计算结果c进栈
			break;
		case '/':				//判定为'/'号
			Pop1(Opnd, a);		//出栈元素a
			Pop1(Opnd, b);		//出栈元素b
			if (a != 0)
			{
				c = b / a;			//计算c
				Push1(Opnd, c);	//将计算结果c进栈
				break;
			}
			else
			{
				printf("nt除零错误!n");
				exit(0);		//异常退出
			}
			break;
		default:				//处理数字字符
			d = 0;				//将连续的数字字符转换成对应的数值存放到d中
			while (*postexp >= '0' && *postexp <= '9')   //判定为数字字符
			{
				d = 10 * d + *postexp - '0';
				postexp++;
			}
			Push1(Opnd, d);		//将数值d进栈

			break;
		}
		postexp++;				//继续处理其他字符
	}
	GetTop1(Opnd, e);			//取栈顶元素e
	DestroyStack1(Opnd);		//销毁栈		
	return e;					//返回e
}

????关键代码讲解

这里主要是讲讲解一下如何去运算，看到【default】分支，当后缀表达式碰到数字字符的时候，这里需要将其转换为数字，也就是 - ‘0’，因为’0’的ASCLL码值为48。假设一个数为1,1的ASCLL码值为49，那么49-48也就是1
主要还是来解释一下为什么d 要乘10，大家可以看到，这是一个while循环，因为这是一个不断在找数字的过程，若是在遍历到数字字符后又遍历到了一个，那要如何运算呢，*10就代表着上一个数字要为十位，而当前遍历数字在转换为数字后是为个位，将遍历到的所有数字字符转换后进行一个相加，最后当遍历到的不是数字字符时，才将此相加完的数放入栈中，然后退出循环去处理下一个字符

????观镜：结果测试

????测试结果展示

首先，就是要在main函数中，传入对应的exp和postexp

尤其是对于这个exp，大家千万不要留空格，否则在中缀转后缀的时候就会出现数组越界异常
也就是因为这几个空格，我调试了一个下午????

char exp[] = "(56 - 20)/(4 + 2)";	//错误！！！
char exp[] = "(56-20)/(4+2)";		//正确！！！

char exp[] = "5+8*2+(3*9+6)*4";
char postexp[MaxSize];
trans(exp, postexp);

printf("中缀表达式为：%sn", exp);
printf("后缀表达式为：%sn", postexp);
printf("表达式的值为：%gn", compvalue(postexp));

这就是最终的结果，看后缀表达式，和我们上面通过堆栈原理分析的完全吻合，大家算出来是这样吗????

????整体代码展示

//求简单表达式的值
#include <stdio.h>
#include <stdlib.h>
#define MaxSize 100
//---------------------------------------------------------
//--运算符栈基本运算---------------------------------------
//---------------------------------------------------------
typedef struct
{
	char data[MaxSize];			//存放运算符
	int top;					//栈顶指针
} SqStack;
void InitStack(SqStack*& s)		//初始化栈
{
	s = (SqStack*)malloc(sizeof(SqStack));
	s->top = -1;
}
void DestroyStack(SqStack*& s)	//销毁栈
{
	free(s);
}
bool StackEmpty(SqStack* s)		//判断栈是否为空
{
	return(s->top == -1);
}
bool Push(SqStack*& s, char e)	//进栈元素e
{
	if (s->top == MaxSize - 1)
		return false;
	s->top++;
	s->data[s->top] = e;
	return true;
}
bool Pop(SqStack*& s, char& e)	//出栈元素e
{
	if (s->top == -1)
		return false;
	e = s->data[s->top];
	s->top--;
	return true;
}
bool GetTop(SqStack* s, char& e)	//取栈顶元素e
{
	if (s->top == -1)
		return false;
	e = s->data[s->top];
	return true;
}
//---------------------------------------------------------

void trans(char* exp, char postexp[])	//将算术表达式exp转换成后缀表达式postexp
{
	char e;
	SqStack* Optr;						//定义运算符栈
	InitStack(Optr);					//初始化运算符栈
	int i = 0;							//i作为postexp的下标
	while (*exp != '')					//exp表达式未扫描完时循环
	{
		switch (*exp)
		{
		case '(':						//判定为左括号
			Push(Optr, '(');				//左括号进栈
			exp++;						//继续扫描其他字符
			break;
		case ')':						//判定为右括号
			Pop(Optr, e);				//出栈元素e
			while (e != '(')				//不为'('时循环
			{
				postexp[i++] = e;			//将e存放到postexp中
				Pop(Optr, e);			//继续出栈元素e
			}
			exp++;						//继续扫描其他字符
			break;
		case '+':						//判定为加或减号
		case '-':
			while (!StackEmpty(Optr))	//栈不空循环
			{
				GetTop(Optr, e);			//取栈顶元素e
				if (e != '(')				//e不是'('
				{
					postexp[i++] = e;		//将e存放到postexp中
					Pop(Optr, e);		//出栈元素e
				}
				else					//e是'(时退出循环
					break;
			}
			Push(Optr, *exp);			//将'+'或'-'进栈
			exp++;						//继续扫描其他字符
			break;
		case '*':						//判定为'*'或'/'号
		case '/':
			while (!StackEmpty(Optr))	//栈不空循环
			{
				GetTop(Optr, e);			//取栈顶元素e
				if (e == '*' || e == '/')	//将栈顶'*'或'/'运算符出栈并存放到postexp中
				{
					postexp[i++] = e;		//将e存放到postexp中
					Pop(Optr, e);		//出栈元素e
				}
				else					//e为非'*'或'/'运算符时退出循环
					break;
			}
			Push(Optr, *exp);			//将'*'或'/'进栈
			exp++;						//继续扫描其他字符
			break;
		default:				//处理数字字符
			while (*exp >= '0' && *exp <= '9') //判定为数字
			{
				postexp[i++] = *exp;
				exp++;
			}
			postexp[i++] = ' ';	//用空格标识一个数值串结束
		}
	}
	while (!StackEmpty(Optr))	//此时exp扫描完毕,栈不空时循环
	{
		Pop(Optr, e);			//出栈元素e
		postexp[i++] = e;			//将e存放到postexp中
	}
	postexp[i] = '';			//给postexp表达式添加结束标识
	DestroyStack(Optr);			//销毁栈		
}
//---------------------------------------------------------
//--操作数栈基本运算---------------------------------------
//---------------------------------------------------------
typedef struct
{
	double data[MaxSize];			//存放数值
	int top;						//栈顶指针
} SqStack1;
void InitStack1(SqStack1*& s)		//初始化栈
{
	s = (SqStack1*)malloc(sizeof(SqStack1));
	s->top = -1;
}
void DestroyStack1(SqStack1*& s)	//销毁栈
{
	free(s);
}
bool StackEmpty1(SqStack1* s)		//判断栈是否为空
{
	return(s->top == -1);
}
bool Push1(SqStack1*& s, double e)	//进栈元素e
{
	if (s->top == MaxSize - 1)
		return false;
	s->top++;
	s->data[s->top] = e;
	return true;
}
bool Pop1(SqStack1*& s, double& e)	//出栈元素e
{
	if (s->top == -1)
		return false;
	e = s->data[s->top];
	s->top--;
	return true;
}
bool GetTop1(SqStack1* s, double& e)	//取栈顶元素e
{
	if (s->top == -1)
		return false;
	e = s->data[s->top];
	return true;
}
//---------------------------------------------------------

double compvalue(char* postexp)	//计算后缀表达式的值
{
	double d, a, b, c, e;
	SqStack1* Opnd;				//定义操作数栈
	InitStack1(Opnd);			//初始化操作数栈
	while (*postexp != '')		//postexp字符串未扫描完时循环
	{
		switch (*postexp)
		{
		case '+':				//判定为'+'号
			Pop1(Opnd, a);		//出栈元素a
			Pop1(Opnd, b);		//出栈元素b
			c = b + a;				//计算c
			Push1(Opnd, c);		//将计算结果c进栈
			break;
		case '-':				//判定为'-'号
			Pop1(Opnd, a);		//出栈元素a
			Pop1(Opnd, b);		//出栈元素b
			c = b - a;				//计算c
			Push1(Opnd, c);		//将计算结果c进栈
			break;
		case '*':				//判定为'*'号
			Pop1(Opnd, a);		//出栈元素a
			Pop1(Opnd, b);		//出栈元素b
			c = b * a;				//计算c
			Push1(Opnd, c);		//将计算结果c进栈
			break;
		case '/':				//判定为'/'号
			Pop1(Opnd, a);		//出栈元素a
			Pop1(Opnd, b);		//出栈元素b
			if (a != 0)
			{
				c = b / a;			//计算c
				Push1(Opnd, c);	//将计算结果c进栈
				break;
			}
			else
			{
				printf("nt除零错误!n");
				exit(0);		//异常退出
			}
			break;
		default:				//处理数字字符
			d = 0;				//将连续的数字字符转换成对应的数值存放到d中
			while (*postexp >= '0' && *postexp <= '9')   //判定为数字字符
			{
				d = 10 * d + *postexp - '0';
				postexp++;
			}
			Push1(Opnd, d);		//将数值d进栈

			break;
		}
		postexp++;				//继续处理其他字符
	}
	GetTop1(Opnd, e);			//取栈顶元素e
	DestroyStack1(Opnd);		//销毁栈		
	return e;					//返回e
}
void test()
{
	char exp[] = "5+8*2+(3*9+6)*4";
	char postexp[MaxSize];
	trans(exp, postexp);

	printf("中缀表达式为：%sn", exp);
	printf("后缀表达式为：%sn", postexp);
	printf("表达式的值为：%gn", compvalue(postexp));
	
}

int main(void)
{
	test();
	return 0;
}

????开战：实战演练【LeetCode习题深入】

明白了如何将一个中缀表达式转换为后缀表达式，并且清楚了如何求值。接下来让我们到力扣上去找道题去练练手吧

原题传送门——逆波兰表达式求值

????题目描述

根据逆波兰表示法，求表达式的值。

有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

注意两个整数之间的除法只保留整数部分。

可以保证给定的逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：

输入：tokens = [“2”,“1”,“+”,“3”,“*”]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = [“4”,“13”,“5”,“/”,“+”]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = [“10”,“6”,“9”,“3”,“+”,“-11”,““,”/“,””,“17”,“+”,“5”,“+”]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

????思路分析

首先对于逆波兰表达式，它其实和二叉树的后续遍历挺像的，大家可以把运算符作为中间节点，按照后序遍历的规则画出一个二叉树。
我们已经了解了它的运算规则，题目已经是一个后缀表达式，所以我们不需要进行繁琐的转换，只要对给出的字符串进行一个遍历，看它是数字还是加减乘除运算符即可

????动画展示

温馨提示，微信手机端看不到

逆波兰表达式

????整体代码展示

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> st;
        for(int i = 0;i < tokens.size(); ++i)
        {
            if(tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/")
            {
                int num1 = st.top();    st.pop();
                int num2 = st.top();    st.pop();

                if(tokens[i] == "+")    st.push(num2 + num1);
                if(tokens[i] == "-")    st.push(num2 - num1);
                if(tokens[i] == "*")    st.push((long long)num2 * num1);
                if(tokens[i] == "/")    st.push(num2 / num1);
            }
            else
            {
                //若为数字字符，则将其转换为数字，方便后续运算
                st.push(stoi(tokens[i]));   
            }
        }
        int ret = st.top();
        st.pop();
        return ret;
    }
};

????重点讲解

代码很简单，就是去遍历给出的这个字符串，判断其为加减乘数四个运算符，是的话就将栈中的头两个元素出栈，进行一个四则运算，但是这里要注意的是因为展示FILO，
你第一个进栈的，也就是第二个出栈的才是第一个操作符
你第二个进栈的，也就是你第一个出栈的是第二个操作符
这个逻辑一定要理清，否则会出现运算问题，可以看到这里的运算num2都是在num1的前面
若不是四个运算符，则将其转换为数字进栈即可，这里用到了一个比较偏僻的函数stoi（），它可以将一个字符转换为数字形式，大家不清楚的可以去了解一下

????归思：总结与提炼

OK，这就是我们今天要讲解的内容，有关数据结构中堆栈应用方面——后缀表达式，你学废了吗????

最后

以上就是标致草莓为你收集整理的数据结构 | 后缀表达式【深入剖析堆栈原理】❓初见：什么是后缀表达式????磨砺：怎样将中缀表达式转换为后缀表达式【⭐⭐⭐⭐⭐】✒闭隐：如何对后缀表达式进行求值？【⭐⭐⭐】????观镜：结果测试????开战：实战演练【LeetCode习题深入】????归思：总结与提炼的全部内容，希望文章能够帮你解决数据结构 | 后缀表达式【深入剖析堆栈原理】❓初见：什么是后缀表达式????磨砺：怎样将中缀表达式转换为后缀表达式【⭐⭐⭐⭐⭐】✒闭隐：如何对后缀表达式进行求值？【⭐⭐⭐】????观镜：结果测试????开战：实战演练【LeetCode习题深入】????归思：总结与提炼所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：数据结构
浏览次数：84 次浏览
发布日期：2024-05-13 21:45:01
本文链接：https://www.kaopuke.com/article/k-p-k_13_u_7_o_26_f0_14_j_22_2.html

概述

堆栈应用之后缀表达式

❓初见：什么是后缀表达式

后缀表达式的优势

????磨砺：怎样将中缀表达式转换为后缀表达式【⭐⭐⭐⭐⭐】

????熟悉规则【重点基础掌握】

????层层剖析【堆栈原理展示】

????手撕代码【不信你看不懂】

✒闭隐：如何对后缀表达式进行求值？【⭐⭐⭐】

????运算规则

????关键代码讲解

????观镜：结果测试

????测试结果展示

????整体代码展示

????开战：实战演练【LeetCode习题深入】

????题目描述

????思路分析

????动画展示

????整体代码展示

????重点讲解

????归思：总结与提炼

最后

评论列表共有 0 条评论

发表评论取消回复

概述

堆栈应用之后缀表达式

❓初见：什么是后缀表达式

后缀表达式的优势

????磨砺：怎样将中缀表达式转换为后缀表达式【⭐⭐⭐⭐⭐】

????熟悉规则【重点基础掌握】

????层层剖析【堆栈原理展示】

????手撕代码【不信你看不懂】

✒闭隐：如何对后缀表达式进行求值？【⭐⭐⭐】

????运算规则

????关键代码讲解

????观镜：结果测试

????测试结果展示

????整体代码展示

????开战：实战演练【LeetCode习题深入】

????题目描述

????思路分析

????动画展示

????整体代码展示

????重点讲解

????归思：总结与提炼

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

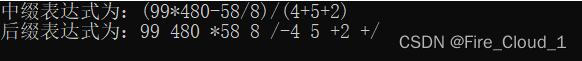
发表评论取消回复