????博客主页:https://blog.csdn.net/WhereIsHeroFrom
????欢迎各位 ????点赞 ⭐收藏 ????评论,如有错误请留言指正,非常感谢!
????本文由 英雄哪里出来 原创,转载请注明出处,首发于 ???? CSDN ????
作者的专栏:
????C语言基础专栏《光天化日学C语言》
????算法进阶专栏《夜深人静写算法》
????C/C++大厂面试专栏《C/C++ 面试 100 例》
????奇奇怪怪的专栏《学姐教我写代码》
文章目录
- 一、前言
- 二、追忆前尘
- 三、初出茅庐
- 第一题
- 第二题
- 四、小试牛刀
- 第三题
- 第四题
- 第五题
- 五、初窥门径
- 第六题
- 第七题
- 六、所向披靡
- 第八题
- 第九题
- 七、无欲无求
- 第十题
一、前言
本文适合对 c c c 语言感兴趣的初学者,文字浅显易懂,没有太多晦涩的言语,也是作者的亲(瞎)身(编)经(乱)历(造),希望对刚入大学,想在程序方面有所建树的有志青年有所帮助。
当然, c c c 语言大佬也可以当成是茶余饭后的调味剂前来消遣,作者在此不做阻止。
二、追忆前尘
- 我刚进入大学的时候,那时候学
c
c
c 语言,全靠有一位学姐带我。

- 可惜由于年代太过久远,她的样子我早已记不得了。
- 咦?
- 前面那位女子好像就是我的学姐!!!

- 额!那个那个… 学姐你不要东张西望了,我在这里……
- em……,可能这么多年过去不认识我了,不过,这不重要!
- 那一年,她告诉我只要做完她的这 10 道题,
c
c
c 语言就算入门了。

- 于是我开始了我的切题生涯,不知不觉切到了 100 题。
- 然后,我发现我爱上了切题,陆陆续续的切,当我切到 1000 题的时候,学姐毕业了,由于我沉迷切题,早就把她 抛之脑后 了。

- 但是,依稀回想起当年她带我的情景,还是意犹未尽……
- 当年的往事如泉涌般涌上心头,恍如隔世……
- 此时,突然耳边传来她的声音……
三、初出茅庐
第一题
- 当时的我是 零基础,也没有上过课,所以学姐说的第一个词我就已经懵逼了。
- INOUT ??? OUTPUT ???
- 于是,这就成了我有生以来做的第一个题:
【例题1】给定 A 和 B , 输出 A 和 B 的和。
- 经过 两个小时 的研究,终于做出来了,代码长这样:
1
2
3
4
5
6
7
8
9#include <stdio.h> // (1) int main() { int a, b; while ( scanf("%d %d", &a, &b) != EOF) { // (2) printf("%dn", a + b); // (3) }; return 0; }
- 1)
stdio.h是最基本的头文件,需要用到的一些输入输出的函数都是在这里声明的,所以需要把它包含进来; - 2)
scanf就是输入函数,因为计算机不知道你要输入的是数字还是字符串还是别的什么东西,所以需要规定输入的格式化类型,%d代表整数,%f代表小数,%s代表字符串等等;因为计算机不知道什么时候结束输入,所以还有个返回值来告诉你不需要再输入了,即如果返回EOF,代表不会再有输入了。这里的EOF其实就是个数字,值为 -1; - 3)
printf就是输出函数,这里就是把a + b的值通过给定的格式输出出来;

- 然后,她开始教我一些简单的语句,例如:分支,循环 等等。
第二题
- 学姐突然说了一堆很奇怪的话,我感觉她在侮辱我!
- 后来一问,才知道,原来这是第二道题。
【例题2】输入一个百分制的成绩 t t t,将其转换成对应的等级,具体转换规则如下:90 ~ 100为 A; 80 ~ 89为 B; 70 ~ 79为 C; 60 ~ 69为 D; 0 ~ 59为 E;
- 查了一下 c 语言课本,发现可以用 i f e l s e if else if else 来做,于是我就开始敲代码,两个小时过去后,代码长这样:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23#include <stdio.h> int main() { int v; while (scanf("%d", &v) != EOF) { if (v < 0 || v > 100) { printf("Score is error!n"); // (1) } else { if (v >= 0 && v <= 59) { printf("En"); // (2) } else if (v == 100) { printf("An"); // (3) } else{ // (4) char c = 'D' - (v - 60) / 10; printf("%cn", c); } } } return 0; }
- 1)分数不在给定范围内;
- 2)分数在 [ 0 , 59 ] [0,59] [0,59],直接输出 ‘E’;
- 3)分数等于 100 100 100,直接输出 ‘A’;
- 4)这时候,我发现 B C D 的范围和字符的关系呈线性,于是稍微玩了一点技巧,因为字符也是有运算的,
'B' + 1 = 'C'以及'C' + 1 = 'D',所以分数和等级的关系可以表示成: - l e v e l = D − v − 60 10 level = D - frac {v - 60} {10} level=D−10v−60
- 通过这道题,我了解了 ASCII 码,你不了解就去百度吧,我那时还没有百度,全靠自己领悟(瞎编)的。
四、小试牛刀


- 你想的没错,学姐应该要给我布置下一道题了 ……
第三题
- 然而… …

- 学姐尴尬的笑了笑,于是又给我布置了一个题:
- 啊? 刚上大学,对这些都没什么概念,于是我就去一家一家酒店跑,并且计算走过的路程。

- 我把方圆 5 公里的酒店都跑遍了。
- 然后学姐告诉我,不是让我真的去找酒店,就是做这个题。
- 我 TM 直呼神奇!


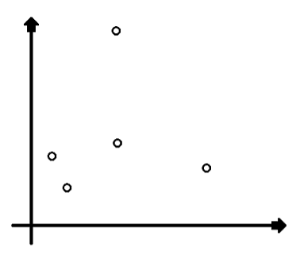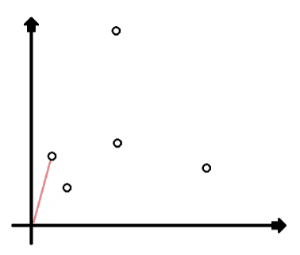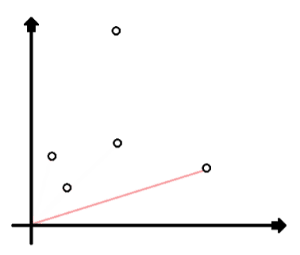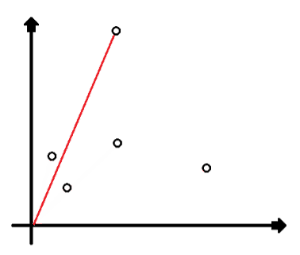
【例题3】给定 n ( n ≤ 1000 ) n(n le 1000) n(n≤1000),然后给出 n n n 个整数坐标 ( x i , y i ) (x_i, y_i) (xi,yi),坐标范围 ( − 100 < x i , y i < 100 ) (-100 < x_i, y_i < 100) (−100<xi,yi<100) 求距离学校最近的坐标的距离,精确到小数点后 3 位(假设 学校的位置在原点)。
- 然后,又过了两个小时,我简直就是天才,两个小时就能做一题,一天 24 小时,也就是一天 12 题,365天就是快 4380 题,是的,当时的菊花还是菊花,当时的我也还比较天真。
- 忘了说代码了,代码长这样:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21#include <stdio.h> #include <math.h> // (1) const int maxd = 1e9; int distSqr(int x, int y) { return x * x + y * y; } int main() { int n, x, y; while (scanf("%d", &n) != EOF) { int minD = maxd; for (int i = 0; i < n; ++i) { // (2) scanf("%d %d", &x, &y); int d = distSqr(x, y); if (d < minD) minD = d; } printf("%.3lfn", sqrt(minD + 0.0)); // (3) } return 0; }
- 1)计算距离需要用到开方,所以需要引用数学库
math.h; - 2)
for(init; condition; action)是 c c c 中基础的循环遍历语句,init部分一般写一些变量初始化;condition是循环得以继续维持的条件判断;action一般是对循环变量进行改变,从而改变condition的真假。循环遍历输入,对输入的坐标选择距离平方最小的。 - 3)由于开方函数比较耗时,不应该放在循环内,所以只需要最后利用
sqrt函数进行一次取值。例如:sqrt(9.0)=3。
第四题

【例题4】给定 n ( 2 ≤ n ≤ 1000 ) n(2 le n le 1000) n(2≤n≤1000),然后给出 n n n 个整数坐标 ( x i , y i ) (x_i, y_i) (xi,yi),坐标范围 ( − 100 < x i , y i < 100 ) (-100 < x_i, y_i < 100) (−100<xi,yi<100),求任意两个坐标中距离最小的,精确到小数点后 3 位。
- 这次我变聪明了,只用了一个小时就做出来了,我真是天才啊!小说都不敢这么写!
- 代码长这样:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28#include <stdio.h> #include <math.h> const int maxn = 1024; const int maxd = 1e9; int distSqr(int x, int y) { return x * x + y * y; } int x[maxn], y[maxn]; int main() { int n; while (scanf("%d", &n) != EOF) { int minD = maxd; for (int i = 0; i < n; ++i) { scanf("%d %d", &x[i], &y[i]); // (1) } for(int i = 0; i < n; ++i) { // (2) for(int j = i + 1; j < n; ++j) { int d = distSqr(x[i], y[i]); if (d < minD) minD = d; } } printf("%.3lfn", sqrt(minD + 0.0)); } return 0; }
- 1)由于要计算任意两点间的距离,所以需要把每个点事先存下来,于是引入了一种新的结构,
c
c
c 语言中,我们称之为 ‘数组’ ,也就是数学意义上的 数列。下标从 0 开始,
a[i]代表第i+1个元素。 - 2)两层循环,计算任意两点间的距离,然后取最小值。
- 我觉得我这个代码很完美,但是学姐却不以为然。
第五题

- 后来我翻了一下书,发现有一种更加好的结构,在
c
c
c 语言里面,它叫 结构体
struct。
【例题5】给定 n ( 2 ≤ n ≤ 1000 ) n(2 le n le 1000) n(2≤n≤1000),然后给出 n n n 个整数坐标 ( x i , y i ) (x_i, y_i) (xi,yi),坐标范围 ( − 100 < x i , y i < 100 ) (-100 < x_i, y_i < 100) (−100<xi,yi<100),求任意两个坐标间距离最小的,精确到小数点后 3 位(利用结构体存储坐标)。
于是代码可以进行如下修改:
1)可以定义一个结构体叫Point,然后把x,y这两个变量放在这个结构体里;
2)两个Point的距离可以定义结构体函数来实现;
- 修改后的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38#include <stdio.h> #include <math.h> const int maxn = 1024; const int maxd = 1e9; int Sqr(int x) { return x * x; } struct Point { int x, y; void read() { scanf("%d %d", &x, &y); // (1) } int distSqr(const Point& o) { // (2) return Sqr(x - o.x) + Sqr(y - o.y); } }P[maxn]; int main() { int n; while (scanf("%d", &n) != EOF) { int minD = maxd; for (int i = 0; i < n; ++i) { P[i].read(); } for(int i = 0; i < n; ++i) { for(int j = i + 1; j < n; ++j) { int d = P[i].distSqr(P[j]); // (3) if (d < minD) minD = d; } } printf("%.3lfn", sqrt(minD + 0.0)); } return 0; }
- 1)将输入的过程抽成
read函数,放在结构体中进行定义; - 2)将计算距离的过程抽成
distSqr函数,放在结构体中进行定义; - 3)典型的结构体成员函数的调用;
当时的我,感觉自己已经是能闭上眼睛手撕十行代码的大神了。
五、初窥门径

- 我傻了!排序是个啥啊??
- 网上搜了下(哦,那时候还没网,聊爆了。。。)
- 我猜 排序,可能是和 排球 差不多的东西吧。
- 然后学姐说:

第六题
【例题6】给定 n ( 2 ≤ n ≤ 1000 ) n(2 le n le 1000) n(2≤n≤1000),然后给出 n n n 个整数坐标 ( x i , y i ) (x_i, y_i) (xi,yi),坐标范围 ( − 100 < x i , y i < 100 ) (-100 < x_i, y_i < 100) (−100<xi,yi<100),求将坐标按照离原点距离从小到大输出。
- 这时候,我接触到了 c++,c++ 里有一个函数叫
sort,调用它就可以轻松对数组的元素进行排序。而且代码也很短,我试着写了一下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39#include <cstdio> #include <cmath> #include <algorithm> // (1) const int maxn = 1024; const int maxd = 1e9; int Sqr(int x) { return x * x; } struct Point { int x, y; int dist; void read() { scanf("%d %d", &x, &y); dist = Sqr(x) + Sqr(y); } bool operator < (const Point& o) const { // (2) return dist < o.dist; } void print() { // (3) printf("%d %dn", x, y); } }P[maxn]; int main() { int n; while (scanf("%d", &n) != EOF) { for (int i = 0; i < n; ++i) { P[i].read(); } std::sort(P, P + n); // (4) for (int i = 0; i < n; ++i) { P[i].print(); } } return 0; }
- 1)
algorithm是 stl 的算法库,用sort函数就需要包含这个库; - 2)官方术语叫:重载操作符,也就是对于这个结构体,需要重载小于号,这样计算机知道按照什么规则进行排序,组合数学里也称为偏序关系。这个题目里,距离小的,即
dist字段小的排在前面; - 3)将
print封装到结构体中,封装一次是c++中的术语; - 4)
std::sort就是排序函数本体了,调用它就能将原数组 P P P 按照dist字段进行递增排序了;
第七题
- 又过了几天。

- 学姐可能只是想单纯鼓励我一下而已。

- 然而,其实这三天,我自己偷偷做了几十个题,所以当她和我说这道题的时候,我已经视其如砍瓜切菜一般。
【例题7】输入一个十进制数 n ( n ≤ 2 30 ) n(n le 2^{30}) n(n≤230),输出它的二进制表示;例如,十进制的 10 ,二进制表示为 1010;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32#include <cstdio> #include <stack> using std::stack; void convert(int n, stack<int>& st) { if (n == 0) st.push(0); while (n) { st.push(n % 2); n /= 2; } } void printStack(stack<int>& st) { while (!st.empty()) { printf("%d", st.top()); st.pop(); } puts(""); } int main() { int n; while (scanf_s("%d", &n) != EOF) { stack <int> st; convert(n, st); // (1) printStack(st); // (2) } return 0; }
- 对于一个 k k k 位的十进制数 n = d 0 d 1 . . . d k − 1 n = d_0d_1...d_{k-1} n=d0d1...dk−1,其中 d 0 d_0 d0 为高位,那么它的表示为:
- n = ∑ i = 0 k − 1 d i 1 0 k − i − 1 n = sum_{i = 0}^{k-1} {d_i}10^{k-i-1} n=i=0∑k−1di10k−i−1
- 转换成二进制采用的是除留余数法,就是不断除 2,余数保留下来,除数继续除,然后将余数逆序输出。由于先除的后输出,所以可以采用栈这种数据结构来保存。

六、所向披靡
- 这时候的我觉得自己所向披靡,感觉应该没有什么题可以难到我了!

第八题
- 计算机中所有的数据二进制的形式存储在设备中。
- 即 0、1 两种状态,计算机对二进制数据进行的运算叫位运算。
- 位运算包括:位与、位或、异或、左移、右移 等等。
【例题8】给定 n ( n ≤ 1 0 7 ) n(n le 10^7) n(n≤107) 个数,求其中是 2 的幂 的数的个数。
- 这个题需要用到 位与(
c
c
c 语言中用
&表示)。所谓位与就是两个数 a a a 和 b b b 的二进制表示的每一位,从低位对位开始做与运算,只有两个位都为1,结果才为1,否则为0。如下所示: - 101001 001101 = 001001 frac {101001}{001101} = 001001 001101101001=001001
- 知道了这个性质以后,2 的 k k k 次幂的二进制表示为 ( 1 00...00 ⏟ k ) 2 (1underbrace {00...00}_{rm k})_2 (1k 00...00)2,而 2 k − 1 2^k-1 2k−1 的二进制表示为 ( 11...11 ⏟ k ) 2 (underbrace {11...11}_{rm k})_2 (k 11...11)2,对这两个数进行位与运算,我们得到的结果为 0,所以一个数是不是 2 的幂,我们只要将它自己和它自己减一做位与运算就能判断了(当然 0 也满足,但它不是 2 的幂,需要排除掉,这里涉及到补码的知识就不再展开了)。
1
2
3
4bool isPowerOfTwo(int n) { return n && ( (n & (n-1)) == 0 ); }

第九题
【例题9】给定 n n n, m m m,请用 O ( 1 ) O(1) O(1) 的时间将一个数 n n n 的二进制第 m m m 位进行翻转。
- 这题主要用到异或(
c
c
c 语言中用
^表示)和左移( c c c 语言中用<<表示)。 - 单个位的异或就是:相同为 0,不同为 1,即 0 x o r 0 = 1 x o r 1 = 0 0 xor 0 = 1 xor 1 = 0 0 xor 0=1 xor 1=0, 1 x o r 0 = 0 x o r 1 = 1 1 xor 0 = 0 xor 1 = 1 1 xor 0=0 xor 1=1;
- 重点就是:无论是 0 还是 1,一旦异或上1,就会进行翻转。一旦异或上0,则结果不变。
- 而左移
x << k的用处就是将 x x x 的二进制所有位整体左移 k k k 位,并且低位补上 k k k 个 0。 - 于是这个问题就可以用以下一行代码解决了。
1
2
3
4int turnOver(int n, int m) { return n ^ (1<<m); }
七、无欲无求
第十题


- 对于当年的我,看到这样的题,就直接哭了,不在我的认知范围内。当然,现在肯定随便切了。我们来看看这个题是怎样求解的。
【例题10】给定 n ( n ≤ 9 ) n(n le 9) n(n≤9), 按字典序输出 1 到 n n n 的所有全排列。
- 全排列的种数是 n ! n! n!,要求按照字典序输出。这是最典型的深搜问题。我们可以把 n n n 个数两两建立无向边(即任意两个结点之间都有边,也就是一个 n n n 个结点的完全图),然后对每个点作为起点,分别做一次深度优先搜索,当所有点都已经标记时,输出当前的搜索路径,就是其中一个排列;
- 这里需要注意的是,回溯的时候需要将原先标记的点的标记取消,否则只能输出一个排列。如果要按照字典序,则需要在遍历的时候保证每次遍历都是按照结点从小到大的方式进行遍历的。
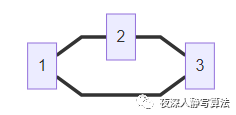
-
如下图所示,代表了一个 3个数的全排列的深度优先搜索空间树;
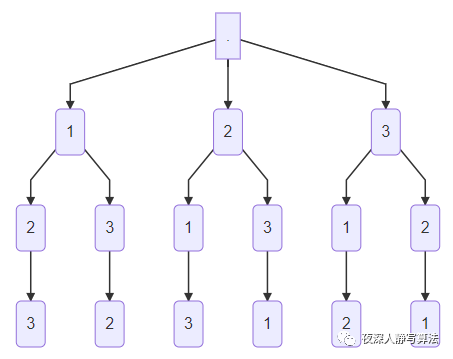
-
C++ 代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15void dfs(int depth) { // 1 if(depth == MAXN) { // 2 dfs_print(); return; } for(int i = 1; i <= MAXN; ++i) { int v = i; if(!visit[v]) { // 3 dfs_add(v); // 4 dfs(depth+1); dfs_dec(v); } } }
- 1)这里的
depth参数用来做计数用,表明本次遍历了多少个结点; - 2)当遍历元素达到
MAXN个的时候,输出访问的元素列表; - 3)
visit[v]用来判断 v v v 这个元素是否有访问过; - 4)
dfs_add和dfs_dec分别表示将结点从访问列表加入和删除;
- 后面的日子,我基本就是和计算机的机房一起度过的,学姐再也没有找过我,我也没有找过她,因为这个故事 TM 就是我瞎编的。

- 最后,祝愿所有学姐都能找到一个好工作!
最后
以上就是甜美刺猬最近收集整理的关于《学姐教我写代码(一)》十道题搞定C语言一、前言二、追忆前尘三、初出茅庐四、小试牛刀五、初窥门径六、所向披靡七、无欲无求的全部内容,更多相关《学姐教我写代码(一)》十道题搞定C语言一、前言二、追忆前尘三、初出茅庐四、小试牛刀五、初窥门径六、所向披靡七、无欲无求内容请搜索靠谱客的其他文章。

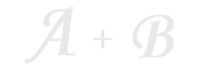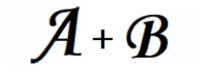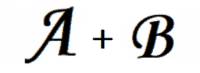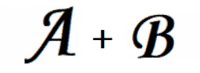








发表评论 取消回复