一般性选择问题（在N个数中选第K大或第K小）

60 阅读 0 评论 40 点赞

我是靠谱客的博主清秀向日葵，最近开发中收集的这篇文章主要介绍一般性选择问题（在N个数中选第K大或第K小），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

问题：选第k小.

输入：数组S，S的长度n，正整数k（1 <= k <= n）.

输出：第k小的数.

算法1：调用k次选最小算法，时间复杂度O(kn)

算法2：先排序，然后输出第k小的数，时间复杂度O(nlogn)

算法3：分治算法

下面我们来讨论算法3.

设计思想（假设数组中数据无重复）：

用数组S中的某个元素m做标准将S划分成S1与S2，其中S1中的元素小于m，S2中的元素大于等于m
如果k <= |S1|,则在S1中找第k小。如果k == |S1| + 1,则m是第k小。如果k > |S1| + 1，则在S2中找第k - |S1| - 1小。（|S1| 表示 S1 中元素的个数）

现在的问题是我们如何选择m使得子问题的规模最小从而使算法效率更高。

我现在举出三种选法：

每次取待测范围开头的元素为m
每次取待测范围的开头，中间，结尾的三个数作比较，取这三个数中的中位数为m
将数组划分为w个小数组，没个小数组的元素个数为p，对每个小数组先进行排序，取出每个小数组的中位数，然后再在这w个小数组的中位数中取中位数作m

我们考虑一个极端情况，如果数组本来就是有序的（但你不知道），对于选法1，每次只能排除一个元素，即没有比m更小的元素了，这样的话算法的时间复杂度为O(kn)，对原有的算法来讲，分治法并没有改进其效率。选法2同理（即在最坏的情况下，也是n^2的时间复杂度，只不过比选法1要好一点）。可以看出选法1和选法2有共同的问题，即在极端情况下子问题的大小较原问题来说几乎不变，我们可以通过分治法的递推方程得分治所得的子问题规模越小，分治法效率越高，对于这个问题来说，若我们每次分治所得的两个子问题都差不多大，即接近于原问题的1/2，效率可达最高。

下面我们分析选法三（以小数组中元素个数p = 5为例）：

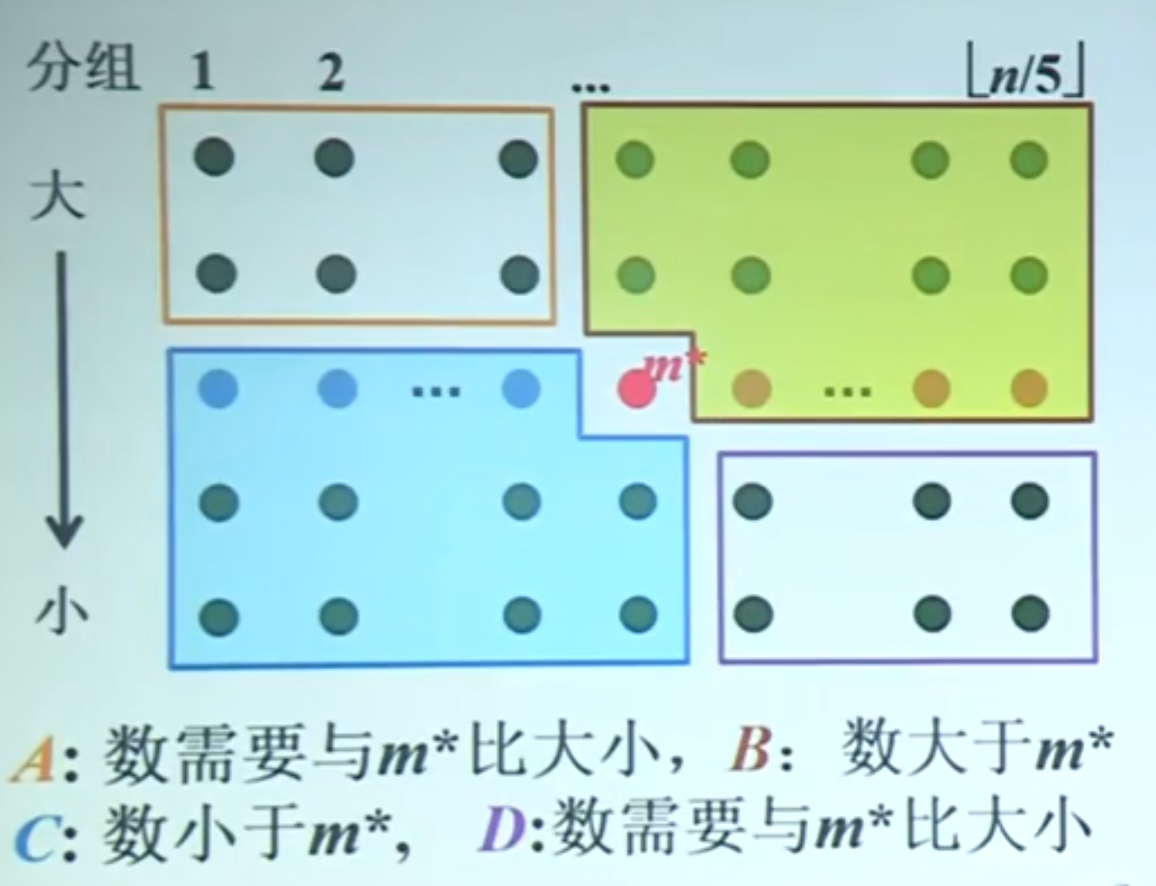
如上图可得，左下角的元素都小于m，右上角的元素都大于m（因为左边小数组的中位数都小于m，每个小数组下面的数又都小于它们的中位数，那某自然也就小于m了右上角同理），这样相当于这两部分的数不用与m作比较，我们只需要将左上角和右下角的元素与m作比较即可将数组划分为S1和S2两部分。

若数组中的数据有重复时，S1中保存的数也有可能等于m，eg:若m所属的那个分组中其余四个数都与m相等，数组中靠后的两个数被划入S1，前两个数被划入S2。

下面我们分析一下子问题的规模，假设划分后小数组的个数为奇数，且S恰好被划分成w个小数组，没有余出，w = 2r + 1,则由下图：

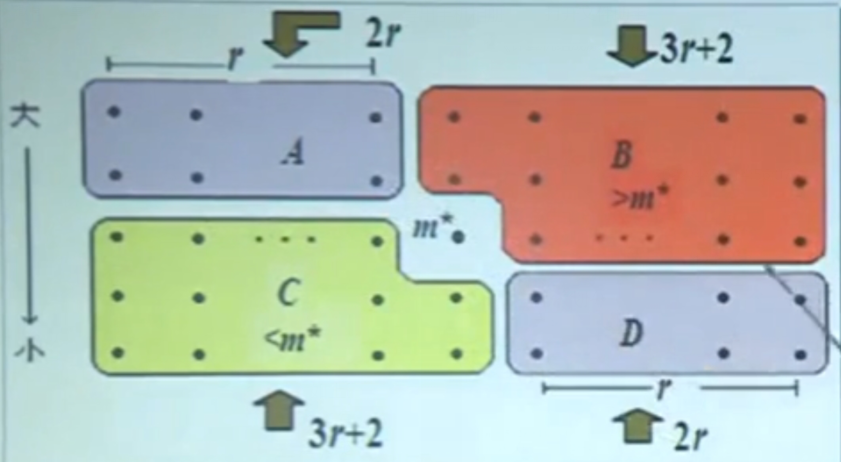
n = 5 * (2r + 1), |A| = |D| = 2r （n是数组S中元素的个数）

子问题规模至多：2r + 2r + 3r + 2 = 7r + 2（当A和D区的数都小于m，即属于S1，且|S1| >= k时或 A和D区的数都大于m，即属于S2且 |S1| + 1 < k 时子问题规模达至最大）

算法的伪代码如图：

算法时间复杂度分析：

求得递推方程后由递归树求出时间复杂度：

可知公比小于1的等比数列收敛于常数，所以时间复杂度为O(n)。

下面我们分析一下分组的时候为什么选5个数为一组，而不是3个或7个？（选奇数个数为一组比偶数要好，因为元素分布更平均）

若选3个元素为一组的话，大家可自行画递归树进行分析，画出来的递归树的公比不小于1，所以3个元素为一组的话算法时间复杂度为O(nlogn).

关键在于：|M| 与规约后子问题问题规模之和小于n，递归树每行的工作量构成公比小于1的等比级数，算法复杂度才是O(n)。

7个元素为一组和5个元素为一组一样，算法时间复杂度都为O(n).

代码：

#include <iostream>
#include <vector>
#include <ctime>
#include <cstdlib>
#include <algorithm>
using namespace std;


//我写的select函数考虑了重复元素的情况，所以和老师讲的代码在细节方面可能会有一些不同

int select(int k, vector<int>& nums) {//返回数组vecotr中第k小的数
	int i = 0, n = nums.size();
	if (k < 1 || k > n) {
		cout << "k取值错误n";
		exit(1);
	}
	if (n <= 5) {//当元素数量小于等于5时直接使用插入排序然后返回
		for (int x = 1; x < n; x++) {
			int t = nums[x];
			for (int y = x; y >= 0; y--) {
				if (y == 0 || t >= nums[y - 1]) {
					nums[y] = t;
					break;
				}
				else nums[y] = nums[y - 1];
			}
		}
		return nums[k - 1];
	}
	vector<int> middle, S1, S2;//三个vector容器分别用来装每个小数组的中位数，小于等于m的数，大于等于m的数
	//分组的整体时间复杂度为O(n/5)
	for (; i + 5 <= n; i += 5) {//以5个元素为一组进行分组，注意到循环结束后，若存在下标大于等于i的元素，则这些元素需单独考虑
		//对分组内的5个元素进行插入排序，由于元素数量固定为5，所以这一步操作的时间复杂度为O(1)
		for (int x = i + 1; x < i + 5; x++) {
			int t = nums[x];
			for (int y = x; y >= i; y--) {
				if (y == i || t >= nums[y - 1]) {
					nums[y] = t;
					break;
				}
				else nums[y] = nums[y - 1];
			}
		}
		middle.push_back(nums[i + 2]);
	}
	int m = select(middle.size() / 2 + 1, middle);//返回middle数组中的中位数
	int e = i;
	for (i = 0; i + 5 <= n; i += 5) {//注意这里在划分S1，S2时为了代码实现的方便，我们将m也一同划分入S2
		if (nums[i + 2] == m) {
			S1.push_back(nums[i]);
			S1.push_back(nums[i + 1]);
			S2.push_back(nums[i + 2]);
			S2.push_back(nums[i + 3]);
			S2.push_back(nums[i + 4]);
		}
		else if (nums[i + 2] > m) {
			S2.push_back(nums[i + 2]);
			S2.push_back(nums[i + 3]);
			S2.push_back(nums[i + 4]);
			if (nums[i] <= m)S1.push_back(nums[i]);
			else S2.push_back(nums[i]);
			if (nums[i + 1] <= m)S1.push_back(nums[i + 1]);
			else S2.push_back(nums[i + 1]);
		}
		else {
			S1.push_back(nums[i]);
			S1.push_back(nums[i + 1]);
			S1.push_back(nums[i + 2]);
			if (nums[i + 3] >= m)S2.push_back(nums[i + 3]);
			else S1.push_back(nums[i + 3]);
			if (nums[i + 4] >= m)S2.push_back(nums[i + 4]);
			else S1.push_back(nums[i + 4]);
		}
	}
	for (; e < n; e++) {//对不属于任何分组的元素单独讨论
		if (nums[e] > m)S2.push_back(nums[e]);
		else S1.push_back(nums[e]);
	}
	int s = S1.size();
	if (s >= k)return select(k, S1);
	else if (s + 1 == k)return m;
	else return select(k - s, S2);//因为m也被划入了S2所以这里是k - s 而不是 k - s - 1
}

void get_data(vector<int>& nums, int n) {//随机生成n个数据，装入nums
	for (int i = 0; i < n; i++)nums.push_back(rand());
}

int main() {
	srand((unsigned int)time(nullptr));
	vector<int> nums;
	cout << "请输入您想生成的数据数量：";
	int n, k;
	cin >> n;
	cout << "您想得到第几小的元素：";
	cin >> k;
	get_data(nums, n);
	cout << "第" << k << "小的数据为" << select(k, nums) << "!n";
	sort(nums.begin(), nums.end());
	for (int i = 0; i < n; i++)cout << nums[i] << ' ';
	return 0;
}