深度学习 - 处理序列的神经网络 (循环、长短时记忆、递归)

循环神经网络 RNN

循环神经网络（Recurrent Neural Network，RNN）是一种对序列数据进行建模的深度学习模型。传统的深度学习模型，诸如 ANN 或 CNN 都只能对定长的数据进行学习，而且即便是可以将变长的数据处理成定长数据，也只能捕捉到数据中的局部特征。而 RNN 则可以处理序列数据，其中每个神经元都可以保存它们之前的序列信息，因此可以对整个序列进行建模，并对数据进行分类或生成新的序列。RNN在机器翻译、语音识别、图像描述和序列标注等多个领域有所应用。

• 结构 and 计算过程

  RNN 的网络结构很简单，如图所示：
  
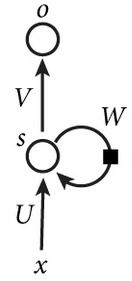
  图中 x 为输入，s 为神经元，o 为输出，W、U、V 为参数矩阵。特殊之处在于 W 矩阵的回乘。

  将 RNN 结构展开之后会更加清晰：
  
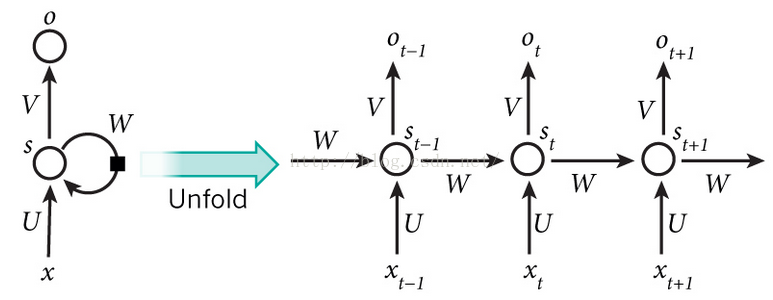
  当中每一个神经元的计算过程如下，其中 $f$ 为激活函数。

  当前神经元的参数值：

  $ne{t}_t=U{x}_t+W{s}_{t-1}$

  $s_t=f(ne{t}_t)$

  当前神经元的输出值：$o_t=f(V{s}_t)$

• 反向传播

  RNN 使用BPTT（Back Propagation Through Time，基于时间的反向传播）算法实现。其实依然是链式求导，没有太大差别。

  模型是要经过训练的，RNN 的训练过程同样使用 梯度下降，不过此时的梯度下降与 $o_t$ 无关，只与 { s 1 , . . . . . . , s t , . . . . . . , s T } {s_1,......, s_{t},......,s_T} {s1​,......,st​,......,sT​} 有关。

  RNN 的梯度可以写成连乘的形式：$\frac{\partial ne{t}_T}{\partial ne{t}_1}=\frac{\partial ne{t}_T}{\partial ne{t}_{T-1}}...\frac{\partial ne{t}_t}{\partial ne{t}_{t-1}}...\frac{\partial ne{t}_2}{\partial ne{t}_1}$

  取其中一项探究：

  $\frac{\partial ne{t}_t}{\partial ne{t}_{t-1}}=\frac{\partial ne{t}_t}{\partial s_{t-1}}\cdot \frac{\partial s_{t-1}}{\partial ne{t}_{t-1}}=W\cdot diag[f^{\prime }(ne{t}_{t-1})]$

  其中 $W\cdot diag[f^{\prime }(ne{t}_{t-1})]$ 的结果：$n\ast n$ 的矩阵为 雅可比矩阵。

  反向传播以偏导数作为误差近似。

• 梯度问题

  • 梯度消失 与 梯度爆炸

    RNN 设计的初衷就是为了捕获数据中长距离的依赖关系，但实践应用中却做不到这一点。主要原因是因为梯度消失问题。

    其中的一项梯度：$\frac{\partial ne{t}_t}{\partial ne{t}_{t-1}}=W\cdot diag[f^{\prime }(ne{t}_{t-1})]$

    那么如果是多个神经元的话，$g=W^n\cdot diag[f^{\prime }(ne{t}_{t-1})]\dots diag[f^{\prime }(ne{t}_i)]\dots diag[f^{\prime }(ne{t}_1)]$，

    根据公式，当雅克比矩阵的特征值大于 1 时，则 梯度 g 会非常大，距离输出层越远的神经元的梯度会越大，导致梯度爆炸，无法收敛；而如果特征值小于 1 时，则梯度 g 会非常小，距离输出层越远的神经元的梯度会越小，导致梯度消失，无法学习。

    因此 RNN 很难对数据中长距离的依赖关系进行学习。

    梯度爆炸可以使用梯度裁剪方法来缓解，即当梯度范式大于某一阈值时，对梯度进行等比收缩。而梯度消失问题则比较棘手，需要对模型本身进行改进。

    对于普通前馈神经网络来讲，深度残差网络可以缓解梯度消失的现象，对于 RNN 来讲，长短时记忆模型（LSTM）则很大程度上弥补梯度消失带来的损失。

  • 激活函数

    ReLU 函数在前馈神经网络中应用非常广泛，它是否也可以应用到 RNN 中呢？

    当然也是可以使用的，只不过我们需要对矩阵初值做一定限制，否则很容易出现数值问题。

    对梯度 $g=W^n\cdot diag[f^{\prime }(ne{t}_{t-1}){]}^n$，激活函数使用 ReLU，且值都大于 0 ，则 $diag[f^{\prime }(ne{t}_{t-1}){]}^n$ 为单位矩阵（导数都为 1），所以 $g=W^n$，此时梯度 g 的情况则完全由 W 来决定。

    如果 $W$ 不是单位矩阵，则 $g=W^n$ 一定是非常小的数 或 非常大的数，仍然会出现梯度问题。所以如果使用 ReLU 作为激活函数，在初始化时应设 W 为单位矩阵。实验结果也证明，初始化 W 为单位矩阵，使用 ReLU 做为激活函数在一些应用中取得了与 LSTM 模型相似的结果，而且学习速度比 LSTM 快。

长短时记忆 LSTM

为了解决 循环神经网络 无法捕获数据长距离依赖的缺陷，产生了 LSTM，其中包含 遗忘门、输入门、输出门 三个门，而且在不同的门使用不同的激活函数以达到不同的目的。

• 结构介绍

  详情请见：结构介绍

• 公式推导

  详情请见：公式推导（前向计算与反向传播）

递归神经网络 RNN

循环神经网络 以及 LSTM 适合处理线性的序列数据，而当序列当中有歧义或存在树形、图形结构时，它们则逊色一些。而递归神经网络专门为此而生。

• 介绍

  详情请见：递归神经网络

最后

以上就是无辜发卡为你收集整理的深度学习 - 处理序列的神经网络 (循环、长短时记忆、递归)的全部内容，希望文章能够帮你解决深度学习 - 处理序列的神经网络 (循环、长短时记忆、递归)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。