本文是[数据结构基础系列(7):图]中第9课时[BFS的应用]的例程。
(程序中graph.h是图存储结构的“算法库”中的头文件,详情请单击链接…)
1、最短路径
问题:求不带权连通图G中从顶点u到顶点v的一条最短路径。
#include <stdio.h>
#include <malloc.h>
#include "graph.h"
typedef struct
{
int data; //顶点编号
int parent; //前一个顶点的位置
} QUERE; //非环形队列类型
void ShortPath(ALGraph *G,int u,int v)
{
//输出从顶点u到顶点v的最短逆路径
ArcNode *p;
int w,i;
QUERE qu[MAXV]; //非环形队列
int front=-1,rear=-1; //队列的头、尾指针
int visited[MAXV];
for (i=0; i<G->n; i++) //访问标记置初值0
visited[i]=0;
rear++; //顶点u进队
qu[rear].data=u;
qu[rear].parent=-1;
visited[u]=1;
while (front!=rear) //队不空循环
{
front++; //出队顶点w
w=qu[front].data;
if (w==v) //找到v时输出路径之逆并退出
{
i=front; //通过队列输出逆路径
while (qu[i].parent!=-1)
{
printf("%2d ",qu[i].data);
i=qu[i].parent;
}
printf("%2dn",qu[i].data);
break;
}
p=G->adjlist[w].firstarc; //找w的第一个邻接点
while (p!=NULL)
{
if (visited[p->adjvex]==0)
{
visited[p->adjvex]=1;
rear++; //将w的未访问过的邻接点进队
qu[rear].data=p->adjvex;
qu[rear].parent=front;
}
p=p->nextarc; //找w的下一个邻接点
}
}
}
int main()
{
ALGraph *G;
int A[9][9]=
{
{0,1,1,0,0,0,0,0,0},
{0,0,0,1,1,0,0,0,0},
{0,0,0,0,1,1,0,0,0},
{0,0,0,0,0,0,1,0,0},
{0,0,0,0,0,1,1,0,0},
{0,0,0,0,0,0,0,1,0},
{0,0,0,0,0,0,0,1,1},
{0,0,0,0,0,0,0,0,1},
{0,0,0,0,0,0,0,0,0}
}; //请画出对应的有向图
ArrayToList(A[0], 9, G);
ShortPath(G,0,7);
return 0;
}附:测试用图结构 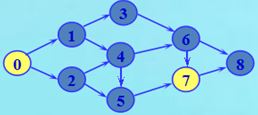
2、最远顶点
问题:求不带权连通图G中,距离顶点v最远的顶点k
#include <stdio.h>
#include <malloc.h>
#include "graph.h"
int Maxdist(ALGraph *G,int v)
{
ArcNode *p;
int i,j,k;
int Qu[MAXV]; //环形队列
int visited[MAXV]; //访问标记数组
int front=0,rear=0; //队列的头、尾指针
for (i=0; i<G->n; i++) //初始化访问标志数组
visited[i]=0;
rear++;
Qu[rear]=v; //顶点v进队
visited[v]=1; //标记v已访问
while (rear!=front)
{
front=(front+1)%MAXV;
k=Qu[front]; //顶点k出队
p=G->adjlist[k].firstarc; //找第一个邻接点
while (p!=NULL) //所有未访问过的相邻点进队
{
j=p->adjvex; //邻接点为顶点j
if (visited[j]==0) //若j未访问过
{
visited[j]=1;
rear=(rear+1)%MAXV;
Qu[rear]=j; //进队
}
p=p->nextarc; //找下一个邻接点
}
}
return k;
}
int main()
{
ALGraph *G;
int A[9][9]=
{
{0,1,1,0,0,0,0,0,0},
{0,0,0,1,1,0,0,0,0},
{0,0,0,0,1,1,0,0,0},
{0,0,0,0,0,0,1,0,0},
{0,0,0,0,0,1,1,0,0},
{0,0,0,0,0,0,0,1,0},
{0,0,0,0,0,0,0,1,1},
{0,0,0,0,0,0,0,0,1},
{0,0,0,0,0,0,0,0,0}
}; //请画出对应的有向图
ArrayToList(A[0], 9, G);
printf("离顶点0最远的顶点:%d",Maxdist(G,0));
return 0;
}附:测试用图结构 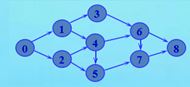
最后
以上就是自觉路人最近收集整理的关于数据结构例程——应用图的广度优先遍历思路求解问题的全部内容,更多相关数据结构例程——应用图内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复