我是靠谱客的博主 义气缘分,这篇文章主要介绍数据结构 · 树T2·旗舰型(存在虚空节点)测试数据(注释里有,这里画个图)(VSC视图太舒服了)啊对对对...T2型·有虚空节点(旗舰)T3 哈弗曼树,现在分享给大家,希望可以做个参考。
T2·旗舰型(存在虚空节点)
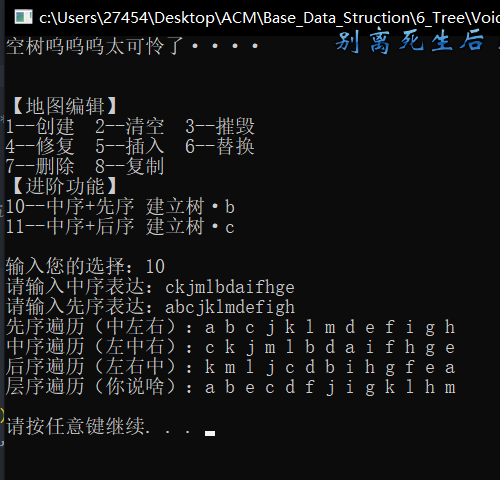
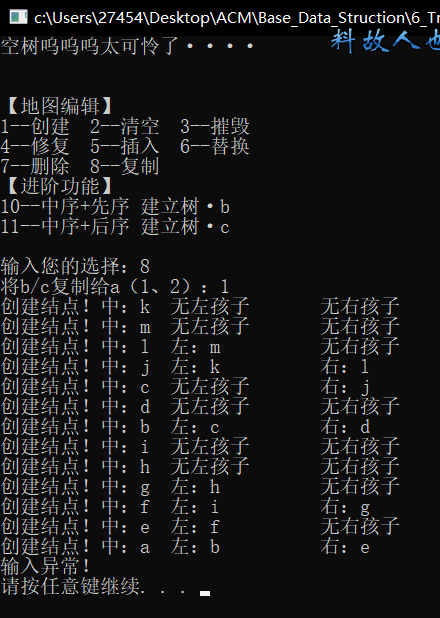
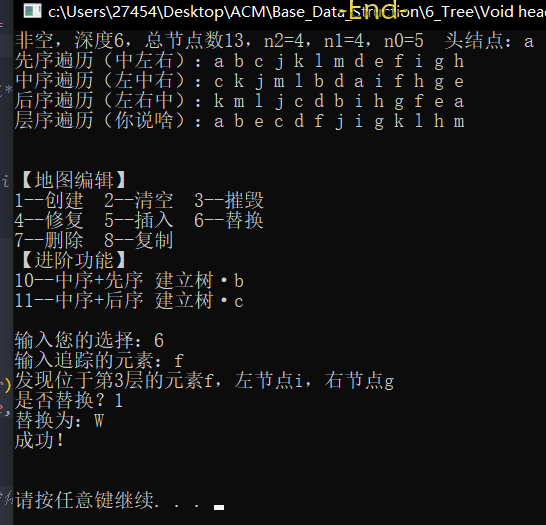
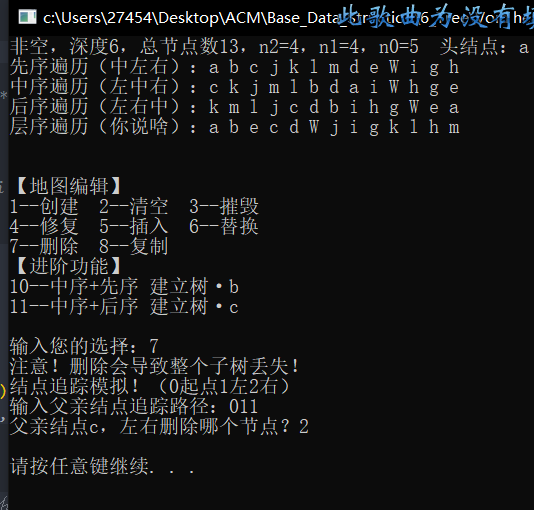
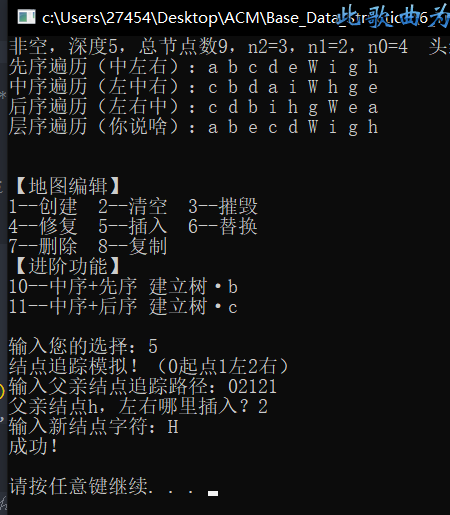
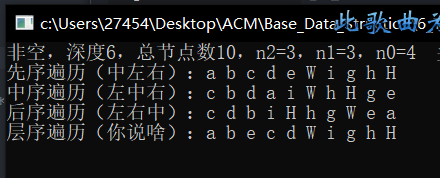
测试数据(注释里有,这里画个图)

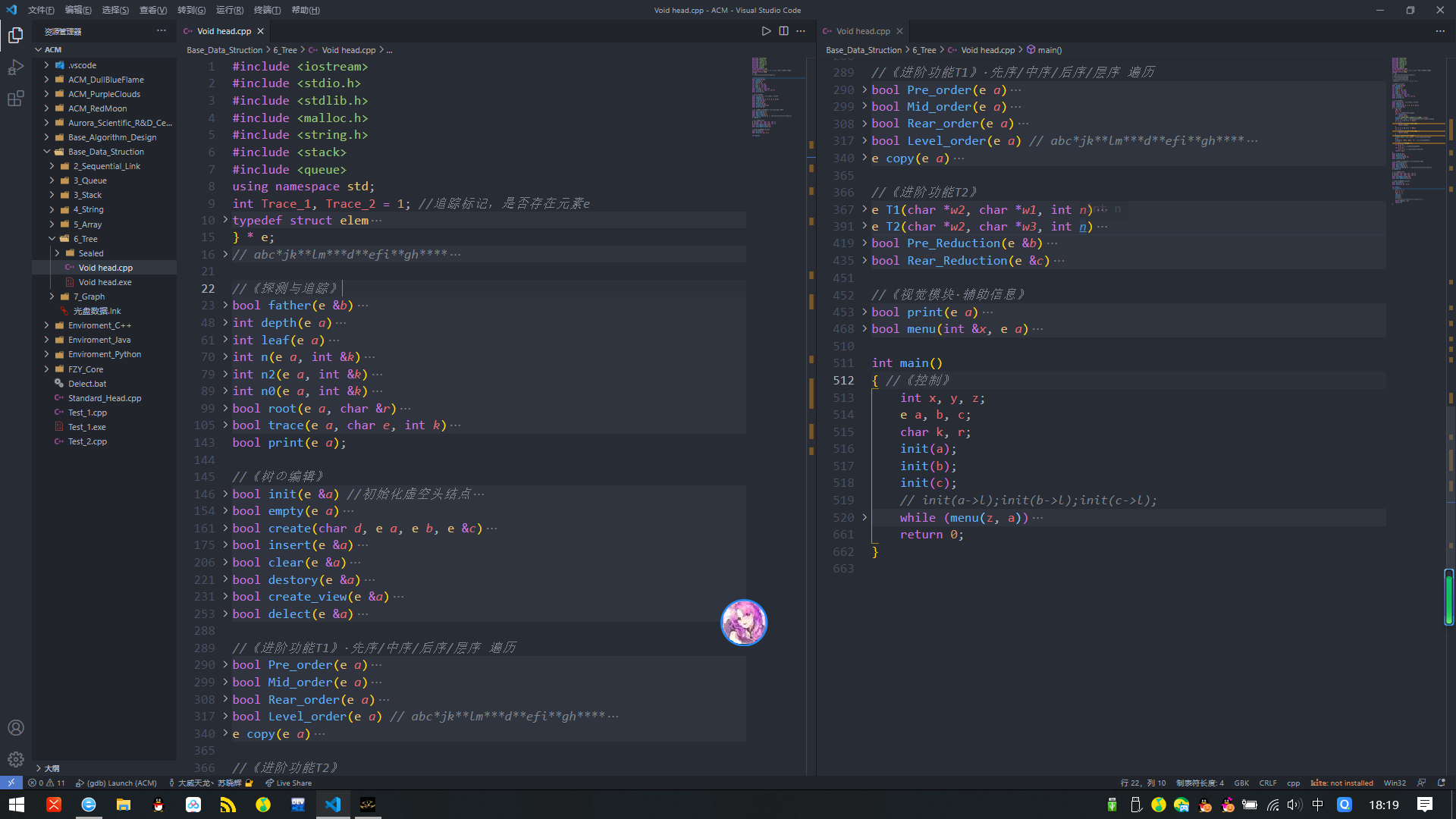
(VSC视图太舒服了)

来康康漂亮姐姐!! 咳咳咳····(夹带私货) 微博@一口音酱
啊
对
对
对
.
.
.
T2型·有虚空节点(旗舰)
鸿蒙纪元·乾坤Day124 2022.01.02更新 已搭载VSCode平台
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <string.h>
#include <stack>
#include <queue>
using namespace std;
int Trace_1, Trace_2 = 1; //追踪标记,是否存在元素e
typedef struct elem
{ //《自定义类型·结点》
char d; //数据域
elem *l, *r; //左右孩子
bool a, b; // true默认为指向子节点
} * e;
// abc*jk**lm***d**efi**gh****
//先序:abcjklmdefigh
//中序:ckjmlbdaifhge
//后序:kmljcdbihgfea
//层序:a b e c d f j i g k l h m
//《探测与追踪》
bool father(e &b)
{ //《追踪·父亲结点》
char xx, q[2745] = {};
int x = 0;
printf("结点追踪模拟!(0起点1左2右)n");
printf("输入父亲结点追踪路径:");
scanf("%c", &xx);
scanf("%s", &q); //抵消回车,输入追踪路径q
//如果只是0那就不检测,根结点就是父亲结点(事实上,第一个字符随便什么都可以)
while (q[++x] != '�' && q[x] != 'n')
{ //《追踪!父亲结点》
if (q[x] == '1' && b->l != NULL) //警惕!这里是字符1,不是数字1(改bug看了好久)
b = b->l; //探测!向左且左节点不空
else if (q[x] == '2' && b->r != NULL)
b = b->r;
else
{
printf("结点路径不存在!n");
return false; //否则·路径异常
}
}
return true;
}
int depth(e a)
{ //《深度》
int d = 0, dl = 0, dr = 0;
if (!a)
d = 0; //没有结点,返回0(父亲结点深度=1(若另一个也是0)因为这时候成为叶子)
else
{
dl = depth(a->l); //递归探底
dr = depth(a->r);
d = 1 + (dl > dr ? dl : dr); //双向表达式,如果成立拿左边,如果不成立拿右边
} //中间表达式可以换,整个括号本质输出一个int数值
return d;
}
int leaf(e a)
{ //《返回·叶子个数》
if (!a)
return 0; //虚空点 ,返回0
else if ((!(a->l)) && (!(a->r)))
return 1; //左右都空 ,返回1
else
return leaf(a->l) + leaf(a->r); //不是叶子,记录左右叶子总和 leaf(l)+leaf(r)
}
int n(e a, int &k)
{ //《返回·节点数》
if (a)
{ //不是虚空点就+1
k++; //中左右探底!
n(a->l, k);
n(a->r, k);
}
}
int n2(e a, int &k)
{ //《返回·节点数》
if (a)
{
if (a->l != NULL && a->r != NULL)
k++; //左右不空+1
n2(a->l, k);
n2(a->r, k);
}
}
int n0(e a, int &k)
{ //《返回·节点数》
if (a)
{
if ((!a->l) && (!a->r))
k++; //左右都不存在
n0(a->l, k);
n0(a->r, k);
}
}
bool root(e a, char &r)
{ //《返回·根结点》
// if(a->l==NULL) return false; //这里没有虚空头结点,直接看a即可
r = a->l->d; // a是虚空结点,它的左节点指向真正的【头结点】
return true;
}
bool trace(e a, char e, int k)
{ //《追踪·修改·先序》
if (a)
{ // k是层数
if (a->d == e)
{ //《中》
Trace_1 = 1;
printf("发现位于第%d层的元素%c,", k, a->d);
if (a->l != NULL)
printf("左节点%c,", a->l->d);
else
printf("无左节点,");
if (a->r != NULL)
printf("右节点%c", a->r->d); //结点信息探测
else
printf("无右节点");
printf("n是否替换?");
int x;
scanf("%d", &x);
if (x == 1)
{ // 124*5**6**37*89**0**
printf("替换为:"); //抵消回车,以后面读入为准(覆盖)
scanf("%c%c", &a->d, &a->d);
printf("成功!n");
}
else
printf("已跳过");
printf("n");
}
k++;
trace(a->l, e, k);
k--; //《左》
k++;
trace(a->r, e, k);
k--; //《右》
}
return true;
}
bool print(e a);
//《树の编辑》
bool init(e &a) //初始化虚空头结点
{ //《初始化》
if (!(a = (e)malloc(sizeof(elem))))
return false;
a->l = NULL;
a->r = NULL;
return true;
}
bool empty(e a)
{ //《判空》
if (a->l == NULL)
return true;
else
return false;
}
bool create(char d, e a, e b, e &c)
{ //《创建·结点》 这个好像不可用
if (!(c = (e)malloc(sizeof(elem))))
exit(1);
c->d = d;
c->l = a;
c->r = b; //新节点赋值
c->a = true;
c->b = true;
if (c)
return true;
else
return false;
}
bool insert(e &a)
{ //《插入》
char xx;
e b = a;
int x; //父亲结点追踪指针
if (!father(b))
return false;
printf("父亲结点%c,左右哪里插入?", b->d);
scanf("%d", &x); //此时b指向父亲结点,x判断插入方向
if (x == 1 && b->l != NULL)
{ //异常
printf("已经存在左子树!n");
return false;
}
if (x == 2 && b->r != NULL)
{ //异常
printf("已经存在右子树!n");
return false;
}
printf("输入新结点字符:");
scanf("%c%c", &xx, &xx); //抵消回车,读入字符xx
e t;
create(xx, NULL, NULL, t); //《创建!新节点》
if (t)
printf("成功!n");
if (x == 1)
b->l = t; //《接入!新节点》
if (x == 2)
b->r = t; // 124*5**6**37*89**0**
return true;
}
bool clear(e &a)
{ //《清除·全树·保留头结点》
if (a->l != NULL)
{ //(没有虚空结点,头结点不会被清算)
clear(a->l); //递归探底
free(a->l); //解放左节点
a->l = NULL; //当前置空
} // 124*5**6**37*89**0**
if (a->r != NULL)
{
clear(a->r);
free(a->r);
a->r = NULL;
}
}
bool destory(e &a)
{ //《摧毁》
if (a->l != NULL)
destory(a->l);
if (a->r != NULL)
destory(a->r);
free(a);
a = NULL;
return true; //解放当前结点,当前指针置空,返回解放完成
}
bool create_view(e &a)
{ //《创建·先序·字符串建立》
char b;
scanf("%c", &b); //无限读入!直到二叉树建立完成()
if (b == '*' || b == 'n')
{
a = NULL;
printf("报空回溯!n");
}
else
{
if (!(a = (elem *)malloc(sizeof(elem))))
return false;
printf(" 放置:%cn", b);
a->d = b; //中间
printf(" 向左!n");
create_view(a->l); //左边
printf(" 向右!n");
create_view(a->r); //右边
}
return true;
}
bool delect(e &a)
{ //《删除》
int x = 0, y, z;
e b = a;
printf("注意!删除会导致整个子树丢失!n"); // 124*5**6**37*89**0**
if (!father(b))
return false;
printf("父亲结点%c,左右删除哪个节点?", b->d);
scanf("%d", &x);
if (x == 1 && b->l == NULL)
{
printf("左结点已空!n");
return false;
}
if (x == 2 && b->r == NULL)
{
printf("右结点已空!n");
return false;
}
if (x == 1)
{
clear(b->l); //删除会导致子树失去联系,所以干脆一起内存放掉算了
free(b->l);
b->l = NULL;
}
else if (x == 2)
{
clear(b->r);
free(b->r);
b->r = NULL;
}
else
printf("失败!n");
return true;
}
//《进阶功能T1》·先序/中序/后序/层序 遍历
bool Pre_order(e a)
{ //《前序遍历》 中左右
if (a)
{
printf("%c ", a->d);
Pre_order(a->l);
Pre_order(a->r);
}
}
bool Mid_order(e a)
{ //《中序遍历》 左中右
if (a)
{
Mid_order(a->l);
printf("%c ", a->d);
Mid_order(a->r);
}
}
bool Rear_order(e a)
{ //《后序遍历》 左右中
if (a)
{
Rear_order(a->l);
Rear_order(a->r);
printf("%c ", a->d);
}
}
bool Level_order(e a) // abc*jk**lm***d**efi**gh****
{
queue<e> q;
q.push(a);
while (1)
{
int n = q.size();
if (n == 0)
break;
while (n--)
{
e t = q.front();
q.pop();
printf("%c ", t->d);
if (t->l)
q.push(t->l);
if (t->r)
q.push(t->r);
}
}
}
e copy(e a)
{ //《复制》
if (!a)
return NULL;
e r, l, b;
if (a->l)
l = copy(a->l); //有左则复制左
else
l = NULL; //否则报告NULL
if (a->r)
r = copy(a->r); //有右则复制右
else
r = NULL;
create(a->d, l, r, b); //创建当前结点(需要左右节点的情报,所以采用后序遍历复制,从下向上)
printf("创建结点!中:%c", b->d);
if (b->l != NULL)
printf(" 左:%c", b->l->d);
else
printf(" 无左孩子");
if (b->r != NULL)
printf(" t右:%cn", b->r->d);
else
printf(" t无右孩子n"); // 124*5**6**37*89**0**
return b;
}
//《进阶功能T2》
e T1(char *w2, char *w1, int n)
{ //《实践者!T1中先序列》
if (n <= 0)
return NULL; // n子树剩余量
char *p = w2;
int k = 0, x; //左中右,开辟追踪(中结点位置)
while (*p != *w1)
{ // w1指向第一个数
p++;
k++;
if (k > n)
{ //异常检测
printf("序列不匹配!n");
Trace_2 = 0; //标记异常(全局)
return NULL;
}
}
e b;
create(*p, NULL, NULL, b);
x = p - w2;
b->l = T1(w2, w1 + 1, x);
b->r = T1(w2 + x + 1, w1 + x + 1, n - x - 1);
return b; // 124*5**6**37*89**0**
}
e T2(char *w2, char *w3, int n)
{ //《实践者!T2中后序列》
if (n <= 0)
return NULL; // n子树剩余量
char *p = w2;
int k = 0, x; //左中右,开辟追踪(中结点位置)
while (*p != *(w3 + n - 1))
{ // w3指向第一个数,+n-1指向最后一个数,*调动本体比对字符
p++;
k++;
if (k > n)
{ //异常检测
printf("序列不匹配!n");
Trace_2 = 0; //标记异常(全局)
return NULL;
}
}
e b; //跳出来时候,p已经指向中序遍历的根节点了呜呜
create(*p, NULL, NULL, b); //给b新建一个结点
x = p - w2; //除去结点,左半边的长度
b->l = T2(w2, w3, x); //找到左子树根节点,递归
b->r = T2(w2 + x + 1, w3 + x, n - x - 1); //启动时,检测指针都在子序列的第一个元素,《为什么!不是w3+x+1》
return b; // 124*5**6**37*89**0**
//看结构 4526 1 79803
// 5462 90873 1
//对于右子树,w2从w2+x+1(1--7)从7开始读取
// w3从w3+x开始读取(9),两个共读取5=10-4-1个
}
bool Pre_Reduction(e &b)
{ //《还原!中序+先序》
char w2[2745] = {}, w1[2745] = {}, g;
char *p2 = w2, *p3 = w1;
int x, y, z;
printf("请输入中序表达:");
scanf("%c%s", &g, &w2);
printf("请输入先序表达:");
scanf("%c%s", &g, &w1);
z = strlen(w2);
if (z != strlen(w1))
return false;
b->l = T1(w2, w1, z); //你给我虚空结点,我帮你创建b->l
if (Trace_2 == 1)
print(b->l);
}
bool Rear_Reduction(e &c)
{ //《还原!中序+后续》
char w2[2745] = {}, w3[2745] = {}, g;
char *p2 = w2, *p3 = w3;
int x, y, z;
printf("请输入中序表达:");
scanf("%c%s", &g, &w2);
printf("请输入后序表达:");
scanf("%c%s", &g, &w3);
z = strlen(w2);
if (z != strlen(w3))
return false;
c->l = T2(w2, w3, z);
if (Trace_2 == 1)
print(c->l);
}
//《视觉模块·辅助信息》
bool print(e a)
{
printf("先序遍历(中左右):");
Pre_order(a);
printf("n");
printf("中序遍历(左中右):");
Mid_order(a);
printf("n");
printf("后序遍历(左右中):");
Rear_order(a);
printf("n");
printf("层序遍历(你说啥):");
Level_order(a);
printf("n");
}
bool menu(int &x, e a)
{ //《菜单》
system("cls");
int w = 0, w0 = 0, w1 = 0, w2 = 0;
char t;
Trace_1 = 0;
Trace_2 = 1;
if (a == NULL)
printf("二叉树被摧毁!n");
else
{
if (empty(a))
printf("空树呜呜呜太可怜了····n");
else
{
printf("非空,"); // 124*5**6**37*89**0**
n(a->l, w);
n2(a->l, w2);
n0(a->l, w0);
w1 = w - w2 - w0;
printf("深度%d,总节点数%d,n2=%d,n1=%d,n0=%d", depth(a->l), w, w2, w1, w0);
if (root(a, t))
printf(" 头结点:%cn", t);
else
printf(" 头结点:空n");
print(a->l);
}
}
printf("nn【地图编辑】n");
printf("1--创建 2--清空 3--摧毁n");
printf("4--修复 5--插入 6--替换n");
printf("7--删除 8--复制n");
printf("【进阶功能】n");
printf("10--中序+先序 建立树·bn");
printf("11--中序+后序 建立树·cn");
printf("n输入您的选择:");
scanf("%d", &x);
if (x == 2745)
return false;
else
return true;
}
int main()
{ //《控制》
int x, y, z;
e a, b, c;
char k, r;
init(a);
init(b);
init(c);
// init(a->l);init(b->l);init(c->l);
while (menu(z, a))
{
switch (z)
{ // abc*jk**lm***d**efi**gh****
case 1:
{ //《创建·先序》
if (a == NULL)
{ //本体被摧毁,包括虚空结点
printf("树已经被摧毁!n");
break;
}
printf("输入先序建立串(以*为空):");
scanf("%c", &k);
create_view(a->l); //挡住回车后读入
break;
}
case 2:
{ //《清空·除了虚空节点》
if (z == 2)
{ //防止输入英文菜单导致case2被错误引导,我不知道bug为什么
printf("你想清空谁?");
scanf("%c%c", &k, &k);
}
if (k == 'a')
{
if (a == NULL)
{ //虚空结点被摧毁
printf("树已经被摧毁!n");
break;
}
clear(a);
}
if (k == 'b')
{
if (b == NULL)
{ //虚空结点被摧毁
printf("树已经被摧毁!n");
break;
}
clear(b);
}
if (k == 'c')
{
if (c == NULL)
{ //虚空结点被摧毁
printf("树已经被摧毁!n");
break;
}
clear(c);
}
break;
}
case 3:
{ //《摧毁·包括虚空节点》
destory(a);
break;
}
case 4:
{ //《初始化·修复虚空头结点》
init(a);
init(b);
init(c);
break;
}
case 5:
{ //《插入》追踪模块不用修改,输入改成a->l即可
if (empty(a))
printf("空树!n");
else
insert(a->l);
break;
}
case 6:
{ //《追踪·替换》
printf("输入追踪的元素:");
scanf("%c%c", &k, &k);
if (empty(a))
printf("空树!n");
else
trace(a->l, k, 1);
if (Trace_1 == 0)
printf("追踪失败!n");
break;
}
case 7:
{ //《删除》
if (empty(a))
printf("空树!n");
else
delect(a->l);
break;
}
case 8:
{ //《复制》
printf("将b/c复制给a(1、2):");
int gg;
scanf("%d", &gg);
clear(a);
if (gg == 1)
a->l = copy(b->l);
if (gg == 2)
a->l = copy(c->l);
else
{
printf("输入异常!");
break;
}
if (a->l != NULL)
{ // 124*5**6**37*89**0**
printf("先序遍历(中左右):");
Pre_order(a->l);
printf("n");
printf("中序遍历(左中右):");
Mid_order(a->l);
printf("n");
printf("后序遍历(左右中):");
Rear_order(a->l);
printf("n");
}
break;
}
case 10:
{ //中+先
Pre_Reduction(b); // 124*5**6**37*89**0**
break;
}
case 11:
{ //中+后
Rear_Reduction(c);
break;
}
default:
{
printf("输入无效!");
break;
}
}
printf("n");
system("pause");
}
return 0;
}
T1型·无虚空结点
初代代码,存在较多瑕疵,已停止维护(鸿蒙纪元·乾坤Day50-Day53)
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
using namespace std;
int asd,asdqwe=1; //追踪标记,是否存在元素e
typedef struct elem{ //《自定义类型·结点》
char d; //数据域
elem *l,*r; //左右孩子
bool a,b; //true默认为指向子节点
}*e;
//bitree指针e TElemType就是char
//birnode元素elem //124*5**6**37*89**0**
//《辅助功能》
bool father (e &b){ //《追踪·父亲结点》
char xx,q[2745]={};int x=0;
printf("结点追踪模拟!(0起点1左2右)n");
printf("输入父亲结点追踪路径:");
scanf("%c",xx);scanf("%s",&q);//抵消回车,输入追踪路径q
//如果只是0那就不检测,根结点就是父亲结点(事实上,第一个字符随便什么都可以)
while(q[++x]!='�'&&q[x]!='n'){ //《追踪!父亲结点》
if (q[x]=='1'&&b->l!=NULL) //警惕!这里是字符1,不是数字1(改bug看了好久)
b=b->l; //探测!向左且左节点不空
else if (q[x]=='2'&&b->r!=NULL)
b=b->r;
else{
printf("结点路径不存在!n");
return false; //否则·路径异常
}
}
return true;
}
bool cret (char d,e a,e b,e &c){ //《创建·结点》 这个好像不可用
if(!(c=(e)malloc(sizeof(elem)))) exit(1);
c->d=d;c->l=a;c->r=b; //新节点赋值
c->a=true;c->b=true;
if(c) return true;
else return false;
}
bool insert (e &a){ //《插入》
char xx; e b=a; int x;//父亲结点追踪指针
if(!father(b)) return false;
printf("父亲结点%c,左右哪里插入?",b->d);
scanf("%d",&x); //此时b指向父亲结点,x判断插入方向
if(x==1&&b->l!=NULL) { //异常
printf("已经存在左子树!n");
return false;
}
if(x==2&&b->r!=NULL){ //异常
printf("已经存在右子树!n");
return false;
}
printf("输入新结点字符:");
scanf("%c%c",&xx,&xx); //抵消回车,读入字符xx
e t; cret(xx,NULL,NULL,t); //《创建!新节点》
if(t) printf("成功!n");
if(x==1) b->l=t; //《接入!新节点》
if(x==2) b->r=t; //124*5**6**37*89**0**
return true;
}
int dep (e a){ //《深度》
int d=0,dl=0,dr=0;
if(!a) d=0;//没有结点,返回0(父亲结点深度=1(若另一个也是0)因为这时候成为叶子)
else{
dl=dep(a->l);//递归探底
dr=dep(a->r);
d=1+ (dl>dr ? dl:dr); //双向表达式,如果成立拿左边,如果不成立拿右边
} //中间表达式可以换,整个括号本质输出一个int数值
return d;
}
int leaf (e a){ //《返回·叶子个数》
if(!a) return 0; //虚空点 ,返回0
else if( ( !(a->l) ) && ( !(a->r) ) ) return 1;//左右都空 ,返回1
else return leaf(a->l)+leaf(a->r); //不是叶子,记录左右叶子总和 leaf(l)+leaf(r)
}
int n (e a,int &k){ //《返回·节点数》
if(a){ //不是虚空点就+1
k++; //中左右探底!
n(a->l,k);
n(a->r,k);
}
}
int n2 (e a,int &k){ //《返回·节点数》
if(a){
if(a->l!=NULL&&a->r!=NULL) k++;//左右不空+1
n2(a->l,k);
n2(a->r,k);
}
}
int n0 (e a,int &k){ //《返回·节点数》
if(a){
if((!a->l) && (!a->r)) k++; //左右都不存在
n0(a->l,k);
n0(a->r,k);
}
}
bool root (e a,char &r){ //《返回·根结点》
//if(a->l==NULL) return false; //这里没有虚空头结点,直接看a即可
r=a->d; return true;
}
//表达式转二叉树并求值,层序遍历,中序线索化
//《基础功能》
bool init (e &a){ //《初始化》
if(!(a=(e)malloc(sizeof(elem)))) return false;
a->l=NULL;a->r=NULL; return true;
}
bool empty (e a){ //《判空·存在BUG》
if(a->l==NULL&&a->r==NULL) return true; //不存在虚空结点时候,头结点是删除不掉的,你没法判断是不是空表
else return false; //单一结点是会返回空的,因为他确实不存在两个子节点
}
bool clear (e &a){ //《清除·全树·保留头结点》
if(a->l!=NULL){//(没有虚空结点,头结点不会被清算)
clear(a->l);//递归探底
free(a->l); //解放左节点
a->l=NULL; //当前置空
} //124*5**6**37*89**0**
if(a->r!=NULL){
clear(a->r);
free(a->r);
a->r=NULL;
}
}
bool des (e &a){ //《摧毁》
if(a->l!=NULL)
des(a->l);
if(a->r!=NULL)
des(a->r);
free(a);a=NULL;
return true; //解放当前结点,当前指针置空,返回解放完成
}
bool cre1 (e &a){ //《创建·先序·字符串建立》
char b; scanf("%c",&b); //无限读入!直到二叉树建立完成()
if(b=='*'||b=='n') {
a=NULL;printf("报空回溯!n");
}
else{
if(!(a=(elem*)malloc(sizeof(elem)))) return false;
printf(" 放置:%cn",b);a->d=b; //中间
printf(" 向左!n");cre1(a->l); //左边
printf(" 向右!n");cre1(a->r); //右边
}
return true;
}
bool order_1 (e a){ //《前序遍历》 中左右
if(a){
printf("%c ",a->d);
order_1(a->l);
order_1(a->r);
}
}
bool order_2 (e a){ //《中序遍历》 左中右
if(a){
order_2(a->l);
printf("%c ",a->d);
order_2(a->r);
}
}
bool order_3 (e a){ //《后序遍历》 左右中
if(a){
order_3(a->l);
order_3(a->r);
printf("%c ",a->d);
}
}
bool order_4 (e a){ //《层序遍历》 左向右 上至下
}
bool trace (e a,char e,int k){ //《追踪·修改·先序》
if(a){//k是层数
if(a->d==e){ //《中》
asd=1;
printf("发现位于第%d层的元素%c,",k,a->d);
if(a->l!=NULL) printf("左节点%c,",a->l->d);
else printf("无左节点,");
if(a->r!=NULL) printf("右节点%c",a->r->d);//结点信息探测
else printf("无右节点");
printf("n是否替换?");int x;scanf("%d",&x);
if(x==1){//124*5**6**37*89**0**
printf("替换为:");//抵消回车,以后面读入为准(覆盖)
scanf("%c%c",&a->d,&a->d);
}
else printf("已跳过");
printf("n");
}
k++;trace(a->l,e,k);k--;//《左》
k++;trace(a->r,e,k);k--;//《右》
}
return true;
}
e copy (e a){ //《复制》
if(!a) return NULL ; e r,l,b;
if(a->l) l=copy(a->l);//有左则复制左
else l=NULL ;//否则报告NULL
if(a->r) r=copy(a->r);//有右则复制右
else r=NULL ;
cret(a->d,l,r,b); //创建当前结点(需要左右节点的情报,所以采用后序遍历复制,从下向上)
printf("创建结点!中:%c",b->d);
if(b->l!=NULL) printf(" 左:%c",b->l->d);
else printf(" 无左孩子");
if(b->r!=NULL) printf(" t右:%cn",b->r->d);
else printf(" t无右孩子n");//124*5**6**37*89**0**
return b;
}
bool del (e &a){ //《删除》
int x=0,y,z;e b=a;
printf("注意!删除会导致整个子树丢失!n");//124*5**6**37*89**0**
if(!father(b)) return false;
printf("父亲结点%c,左右删除哪个节点?",b->d);scanf("%d",&x);
if(x==1&&b->l==NULL) {
printf("左结点已空!n");
return false;
}
if(x==2&&b->r==NULL){
printf("右结点已空!n");
return false;
}
if(x==1){
clear(b->l); //删除会导致子树失去联系,所以干脆一起内存放掉算了
free(b->l);
b->l=NULL;
}
if(x==2){
clear(b->r);
free(b->r);
b->r=NULL;
}
printf("成功!n");
return true;
return true;
}
bool print (e a);
//124*5**6**37*89**0**
//《强化功能》
e T1(char *w2, char *w1, int n){ //《实践者!T1中先序列》
if(n <= 0) return NULL; //n子树剩余量
char *p = w2; int k=0,x; //左中右,开辟追踪(中结点位置)
while(*p!=*w1){ //w1指向第一个数
p++;k++;
if(k>n){//异常检测
//printf("序列不匹配!n");
asdqwe=0; //标记异常(全局)
return NULL;
}
} e b; cret(*p,NULL,NULL,b);
x = p - w2;
b->l = T1(w2, w1+1, x);
b->r = T1(w2+x+1,w1+x+1,n-x-1);
return b;//124*5**6**37*89**0**
}
e T2(char *w2, char *w3, int n){ //《实践者!T2中后序列》
if(n <= 0) return NULL; //n子树剩余量
char *p = w2; int k=0,x; //左中右,开辟追踪(中结点位置)
while(*p!=*(w3+n-1)){ //w3指向第一个数,+n-1指向最后一个数,*调动本体比对字符
p++;k++;
if(k>n){//异常检测
printf("序列不匹配!n");
asdqwe=0; //标记异常(全局)
return NULL;
}
}
e b;//跳出来时候,p已经指向中序遍历的根节点了呜呜
cret(*p,NULL,NULL,b); //给b新建一个结点
x = p - w2; //除去结点,左半边的长度
b->l = T2(w2, w3, x);//找到左子树根节点,递归
b->r = T2(w2+x+1,w3+x, n-x-1);//启动时,检测指针都在子序列的第一个元素,《为什么!不是w3+x+1》
return b;//124*5**6**37*89**0**
//看结构 4526 1 79803
// 5462 90873 1
//对于右子树,w2从w2+x+1(1--7)从7开始读取
//w3从w3+x开始读取(9),两个共读取5=10-4-1个
}
bool preX (e &b){ //《还原!中序+先序》
char w2[2745]={}, w1[2745]={},g;
char *p2=w2 , *p3=w1; int x,y,z;
printf("请输入中序表达:");scanf("%c%s",&g,&w2);
printf("请输入先序表达:");scanf("%c%s",&g,&w1);
z=strlen(w2);if(z!=strlen(w1)) return false;
b=T1(w2,w1,z);
if(asdqwe==1) print(b);
}
bool rearX (e &c){ //《还原!中序+后续》
char w2[2745]={}, w3[2745]={},g;
char *p2=w2 , *p3=w3; int x,y,z;
printf("请输入中序表达:");scanf("%c%s",&g,&w2);
printf("请输入后序表达:");scanf("%c%s",&g,&w3);
z=strlen(w2);if(z!=strlen(w3)) return false;
c=T2(w2,w3,z);
if(asdqwe==1) print(c);
}
bool preF (e &a){ //《还原!前缀式》
}
bool inF (e &a){ //《还原!中缀式》
}
bool rearF (e &a){ //《还原!后缀式》
}
bool thread (e &a){ //《中序·线索化》
}
//《视觉模块·辅助信息》
bool print (e a){
printf("先序遍历(中左右):");order_1(a);printf("n");
printf("中序遍历(左中右):");order_2(a);printf("n");
printf("后序遍历(左右中):");order_3(a);printf("n");
}
bool menu(int &x,e a){ //《菜单》
system("cls"); //前中后序,选择一种打印方式
//printf("《二叉树 · 综合实现》(无虚空头结点)(测试版本T1)n");
//printf("『鸿蒙纪元☆乾坤』Day50--Daynn");
int w=0,w0=0,w1=0,w2=0; char t; asd=0;asdqwe=1;
if(a==NULL) printf("二叉树被摧毁!n");
else{
n(a,w); n2(a,w2); n0(a,w0); w1=w-w2-w0;
if(empty(a)) printf("空表,");
else printf("非空,");//124*5**6**37*89**0**
printf("深度%d,总节点数%d,n2=%d,n1=%d,n0=%d",dep(a),w,w2,w1,w0);
if(root(a,t)) printf(" 头结点:%cn",t);
else printf(" 头结点:空n");
print(a);
} printf("1--创建 2-清空a 3--摧毁 4-修复n");
printf("5--插入 6-追踪 7--删除 8-复制n");
printf("9--先序建树b 10-后序建树cn");
printf("11-前缀转生b 12-后缀转生cn");
printf("13-更迭(b或c替换a) 14-中缀转生cn");
printf("15-中序线索化n");
printf("输入您的选择:");scanf("%d",&x);
if(x==2745) return false;
else return true ;
}
int main(){ //《控制》
int x,y,z; e a,b,c; init(a);init(b);init(c); char k,r;
while(menu(z,a)){
switch(z){
case 1:{
if(a==NULL){
printf("树已经被摧毁!n");
break;
}
printf("输入先序建立串(以*为空):");
scanf("%c",&k);cre1(a);//挡住回车后读入
break;
}
case 2:{
if(a==NULL){
printf("树已经被摧毁!n");
break;
}
clear(a);
break;
}
case 3:{
des(a);
break;
}
case 4:{
init(a);init(b);
break;
}
case 5:{
insert(a);
break;
}
case 6:{//124*5**6**37*89**0**
printf("输入追踪的元素:");scanf("%c%c",&k,&k);
trace(a,k,1);
if(asd==0) printf("追踪失败!n");
break;
}
case 7:{
del(a);
break;
}
case 8:{
b=copy(a);
if(b!=NULL){ //124*5**6**37*89**0**
printf("先序遍历(中左右):");order_1(b);printf("n");
printf("中序遍历(左中右):");order_2(b);printf("n");
printf("后序遍历(左右中):");order_3(b);printf("n");
}
break;
}
case 9:{//中+先
preX(b);
break;
}
case 10:{//中+后
rearX(c);
break;
}
case 11:{//前缀专转二叉树
preF(b);
break;
}
case 12:{//后缀转二叉树
rearF(c);
break;
}
case 13:{//更迭
printf("调用b还是c(以替换a)?");
scanf("%c%c",&k,&k);//挡住回车
if(k=='b'){
des(a);init(a);a=copy(b);
}
if(k=='c'){
des(a);init(a);a=copy(c);
}
break;
}
case 14:{//中缀转二叉树
inF(c);
break;
}
case 15:{//线索化
thread(a);
break;
}
default:printf("输入无效!");break;
}
printf("n");system("pause");
}
return 0;
}
挖坑(不打算填)
中序线索化的生成与优化检索(看懂即可)
表达式转二叉树并计算(3种),层序遍历,镜像树
T3型森林通过孩子-兄弟结构转为二叉树(综合
T3 哈弗曼树
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define max 2745
int code[max] = {}, k = 0, wpl = 0, c; // k字符转编码 c目标字符的ASCII %d数值
bool here = false;
// 7 6 a 1 b 3 c 7 d 4 e 9 f 8 g
//如果输入的编码是异常的,这个无法测出来,是一个bug
typedef struct HFM
{
int weight; //自身权值
char name; //自字母
HFM *l, *r; //哈夫曼树的左右孩子指针
HFM *next; //哈夫曼树的结点同时又是单链表的结点,next为单链表的结点指针
} * H;
//实践区
bool search(H T)
{ //《打印!先序追踪》
if (T)
{
int y;
if (!(T->l) && !(T->r)) //这是个叶子,有字母
{
y = T->name;
if (c == y)
{
for (int x = 1; x <= k; x++)
printf("%d", code[x]);
here = true; //标记找到
printf(" ");
}
}
code[++k] = 0;
search(T->l);
k--;
code[++k] = 1;
search(T->r);
k--;
}
}
void n0(H &leaf)
{ //《生成!leaf结点》
leaf = (HFM *)malloc(sizeof(HFM));
scanf("%d%c%c", &leaf->weight, &leaf->name, &leaf->name); //抵消空格
leaf->l = NULL;
leaf->r = NULL;
leaf->next = NULL;
}
void n2(H &p, H &q, H &head, H &sum)
{ //《哈夫曼!取出生成》
p = head->next;
q = p->next; // p第一点·q第二点·两点取出·
head->next = q->next; //头指针指向第三点
sum = (HFM *)malloc(sizeof(HFM)); //生成父结点
sum->weight = p->weight + q->weight; //权值
sum->l = p; // T1为左
sum->r = q; // T2为右
sum->name = '�'; //赋值为空
q = head; //比较准备!q是前部,p是后部,准备插入sum
p = q->next;
}
//核心区
H Priority_Link(int n)
{ //《生成!升序链表》·用链表模拟优先队列
HFM *head, *p, *q, *leaf;
head = (HFM *)malloc(sizeof(HFM));
n0(leaf);
head->next = leaf; // head->weight=-1;
for (int x = 2; x <= n; x++)
{
n0(leaf);
q = head;
p = head->next;
// printf("nn当前链表:");pr(head);
// printf("当前叶子%dn",leaf->weight);
while (p != NULL)
{ //生成结点·部署PQ·p指向首元素·q指向首元素之前一个元素
// printf("循环启动!n");
if ((leaf->weight) > (p->weight))
{ // leaf偏大·继续往下找
q = p; // printf(" 偏大惹呜呜n");
p = p->next;
}
else
{ // leaf偏小·掰开插入
// printf(" 可以插入%d %d之间n",q->weight,p->weight);
q->next = leaf; //前端Q·next·接入leaf
leaf->next = p; // leaf接入p
break; //《完成插入就跳出,否则会一直找到null》
}
}
// if(p!=NULL)printf("遍历结束%dn",p->weight);
// else printf("P置空了!n");
if (p == NULL)
{ //尾部插入
q->next = leaf; //最后一个元素看Q
leaf->next = p;
// if(p!=NULL)printf("尾部插入~%d %d %dn",leaf->weight,q->weight,p->weight);
// else printf("尾部插入接入NULLn");
}
}
return head; //返回升序单链表的头指针结点
}
H HFM2(H head)
{ //《生成!哈夫曼树》
HFM *p, *q, *sum; //从小到大遍历单链表
while (head->next != NULL)
{ //链表非空
n2(p, q, head, sum); //删除2点·生成sum
while (p != NULL)
{ //把sum插回去
if (sum->weight > p->weight)
{
q = p;
p = p->next;
}
else
{
q->next = sum;
sum->next = p;
break;
}
}
if (q != head && p == NULL)
{ //把sum插回去
q->next = sum;
sum->next = p;
}
}
return sum; //取出俩结点,head->next指向T3点。全部取出,T3指向NULL,则终结跳出,返回sum(根结点)
}
//引导区
bool print(H T)
{ //《打印!先序追踪》
if (T)
{
if (!(T->l) && !(T->r))
{
printf("字母:%c 权值:%d code:", T->name, T->weight);
for (int x = 1; x <= k; x++)
printf("%d", code[x]);
printf("n");
wpl += k * (T->weight);
}
code[++k] = 0;
print(T->l);
k--;
code[++k] = 1;
print(T->r);
k--;
}
}
bool change_1(HFM *name)
{ //《前缀码·转字母》
char xx, q[2745] = {};
int x = -1;
HFM *temp = name;
printf("输入前缀码:");
scanf("%s", &q); // 7 6 f 7 g 1 weight 5 e 4 d 3 c 2 name
while (q[++x] != '�' && q[x] != 'n')
{
if (q[x] == '0' && name->l != NULL)
name = name->l;
else if (q[x] == '1' && name->r != NULL)
name = name->r;
else
{
printf("方向异常!!n");
return false; //否则·路径异常
}
if (!(name->l) && !(name->r))
{
printf("%c", name->name);
name = temp;
}
}
return true;
}
bool change_2(HFM *name)
{ //《字母·转前缀码》
char w[2745] = {};
int x;
printf("nn输入一串字符:");
scanf("%s", &w);
for (x = 0; x < strlen(w); x++)
{
here = false;
k = 0;
c = w[x];
search(name);
if (!here)
{
printf("n异常!不存在该字符!!");
return false;
}
}
return true;
}
int main()
{
HFM *T;
int n;
char weight[max] = {};
printf("叶子结点个数:");
scanf("%d", &n);
printf("对应权值+字母(隔空):");
T = Priority_Link(n);
T = HFM2(T); //《哈夫曼生成》
printf("先序 · 哈夫曼:n");
print(T);
printf("WPL=%dnn", wpl);
change_1(T);
change_2(T);
system("pause");
return 0;
}
如果输入的编码是错误的,不会识别出来,这是个bug
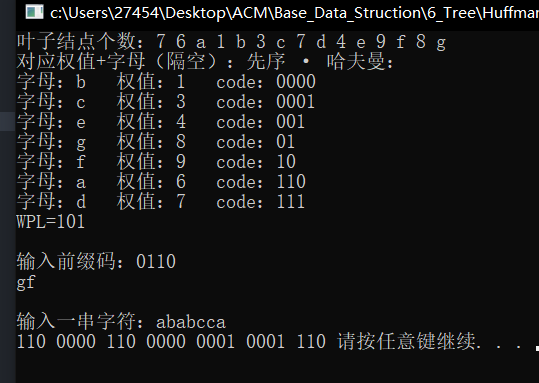
最后
以上就是义气缘分最近收集整理的关于数据结构 · 树T2·旗舰型(存在虚空节点)测试数据(注释里有,这里画个图)(VSC视图太舒服了)啊对对对...T2型·有虚空节点(旗舰)T3 哈弗曼树的全部内容,更多相关数据结构内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复