【图解数据结构】二叉树的概念、性质、结构

概念

一棵二叉树是结点的一个有限集合，该集合:

1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

二叉树是有序树。

对于任意的二叉树都是由以下几种情况复合而成的：

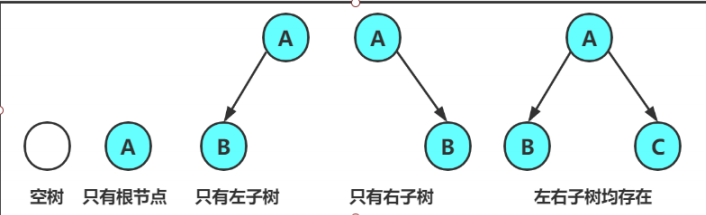
特殊二叉树

满二叉树

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是 ，则它就是满二叉树。

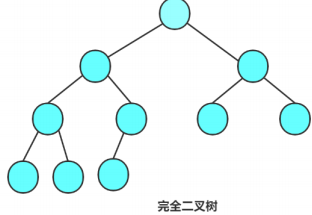
完全二叉树

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

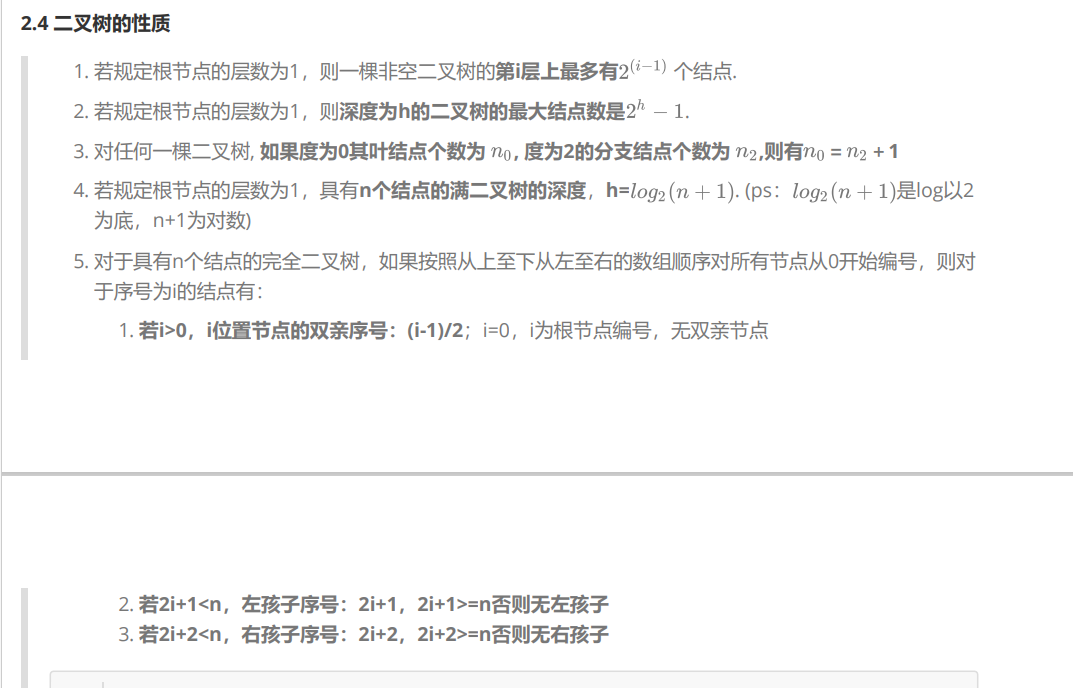
二叉树性质

二叉树存储结构

二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。

下面将先重点讲解 顺序存储。

顺序存储

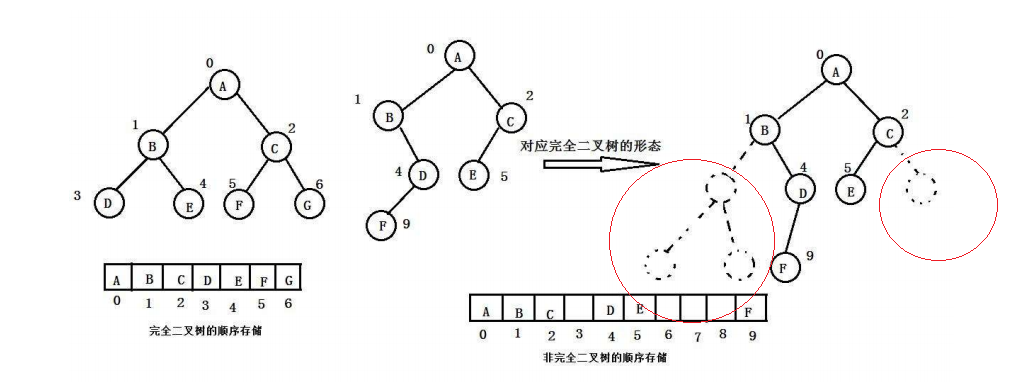
顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。

而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

链式存储

二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链。

（这里暂时不细讲）

二叉树顺序结构及实现

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。

现实中通常把堆使用顺序结构的数组来存储。这里的堆不同于操作系统的虚拟进程空间中的堆。（一个是数据结构，一个是操作系统中管理内存的一块区域分块）。

堆

堆的概念

堆的具体实现会在后续章节逐步展开。

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树。
• 有大堆和小堆

1. 大堆：树中一个树及子树中，任何一个父亲都大于等于孩子
2. 小堆：树中一个树及子树中，任何一个父亲都小于等于孩子。

逻辑结构&存储结构

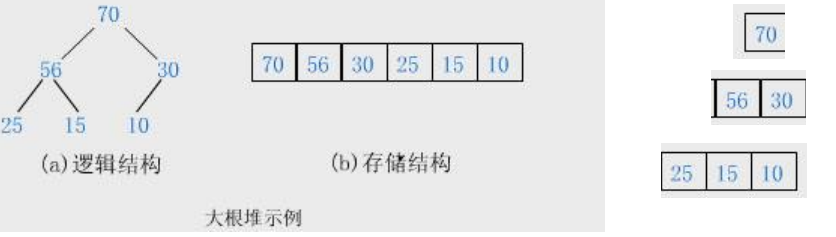
堆的逻辑结构是一个完全二叉树。

堆的存储结构是一个顺序表。

大堆示例

码文不易，欢迎指正！深鞠躬

最后

以上就是还单身百褶裙为你收集整理的【图解数据结构】二叉树的概念、性质、结构的全部内容，希望文章能够帮你解决【图解数据结构】二叉树的概念、性质、结构所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。