1. 首页
  2. 文章中心
  3. 数据结构

数据结构_二叉树_属性-构建-遍历一、二叉树的属性二、二叉树的树节点三、二叉树构建与遍历参考

71 阅读 0 评论
我是靠谱客的博主 迅速毛豆，最近开发中收集的这篇文章主要介绍数据结构_二叉树_属性-构建-遍历一、二叉树的属性二、二叉树的树节点三、二叉树构建与遍历参考，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

一、二叉树的属性

  • 1)二叉树的第i层至多有 2 i − 1 2^{i-1} 2i−1个节点
  • 2)深度为h的二叉树至多有 2 h − 1 2^h-1 2h−1个节点
    • 基于等比序列和计算: s n = a 1 ( 1 − q n ) 1 − q s_n = frac{a_1(1-q^n)}{1-q} sn​=1−qa1​(1−qn)​
  • 3)对于任何一颗二叉树,若它含有n0个叶子节点, n2个度为2的节点,则存在两者的关系 n 0 = n 2 + 1 n_0=n_2+1 n0​=n2​+1
    • 节点数 n = n0+n1+n2
    • 边数 2 n 2 + 1 n 1 = n − 1 2n_2+1n_1 = n - 1 2n2​+1n1​=n−1
      => 2 n 2 + n 1 = n 0 + n 1 + n 2 − 1 2n_2+n_1 = n_0 + n_1 + n_2 - 1 2n2​+n1​=n0​+n1​+n2​−1
      => n 0 = n 2 + 1 n_0=n_2+1 n0​=n2​+1
  • 4)具有n个节点的完全二叉树的深度为floor(log2(n)) + 1
  • 5)若对含n个节点的完全二叉树从上到下且从左到右进行1到n编码,则对完全二叉树中
    任意一个编号为i的节点:
    • 若i=1,则节点是二叉树的跟, floor(i/2)为其父节点
    • 若 2 ∗ i > n 2*i>n 2∗i>n, 则该节点无左孩子, 否则编码2i的节点为其左孩子节点
    • 若 2 ∗ i + 1 > n 2*i+1>n 2∗i+1>n, 则该节点为右孩子, 否则编码2i+1的节点为其右孩子节点

例题

若一个完全二叉树 n=1450 个结点数，
则度为1的节点数n1？
度为2的节点数n2？
叶子节点数n0？
有多少左孩子，多少右孩子，树的高度是多少？

import math
n=1450
# 树高
tree_depth = math.floor(math.log2(n)) + 1
# 倒数第二层全都是n2- n2个数最大值
n2_max = math.pow(2, tree_depth-1) - 1
# 完全二叉树总n
compelet_n = math.pow(2, tree_depth) - 1

# 最后层
n0_part1 = n - n2_max
# 倒数第二层
n0_part2 = math.floor((compelet_n - n)/2)
n0 = n0_part1 + n0_part2
n1 = 1
n2 = n - n0 - n1
left_ = 1 + n2
right_ = n2
print(f"n0={n0}, n1={n1}, n2={n2}, left_={left_}, right_={right_}")

"""
n0=725.0, n1=1, n2=724.0, left_=725.0, right_=724.0
"""

二、二叉树的树节点

主要就是一个节点，存在两个指针可以指向左右子树。

2.1 cpp

#include <iostream>
using namespace std;

template<typename T>
struct  treeNode{
    T data;
    treeNode *left;
    treeNode *right;

    treeNode(T const & data) : data(data){
        left = nullptr;
        right = nullptr;
    }
};


int main(){
    treeNode<int> *tree = new treeNode<int>(10);
    treeNode<int> *left_ = new treeNode<int>(20);
    treeNode<int> *right_ = new treeNode<int>(30);
    tree->left = left_;
    tree->right = right_;
    cout << "tree->data " << tree->data << endl;
    cout << "tree->left->data " << tree->left->data << endl;
    cout << "tree->right->data " << tree->right->data << endl;
}

2.2 python


class treeNode:
    def __init__(self, data, left=None, right=None):
        self.data = data
        self.left = left
        self.right = right

    def __str__(self):
        return f'<data: {self.data} (left:{self.left}; right:{self.right};)>'

    def __repr__(self):
        return str(self)

tree = treeNode(
    "A",
    left=treeNode('B', 
              left=treeNode('D', right=treeNode('G'))),
    right=treeNode('C', left=treeNode('E', right=treeNode('H')), right=treeNode('F'))
)
tree
"""
<data: A (left:<data: B (left:<data: D (left:None; right:<data: G (left:None; right:None;)>;)>; right:None;)>; right:<data: C (left:<data: E 
(left:None; right:<data: H (left:None; right:None;)>;)>; right:<data: F (left:None; right:None;)>;)>;)>
"""

三、二叉树构建与遍历

3.1 树构建

基于完全二叉树的编号顺序输入节点，构建二叉树，空节点名称为^
输入如下:
string name_q[7] = {"aa", "bb", "cc", "dd", "ee", "ff", "^"};
int value_q[7] = {1, 2, 3, 4, 5, 6, 0};
可以直接看书中的构建方法
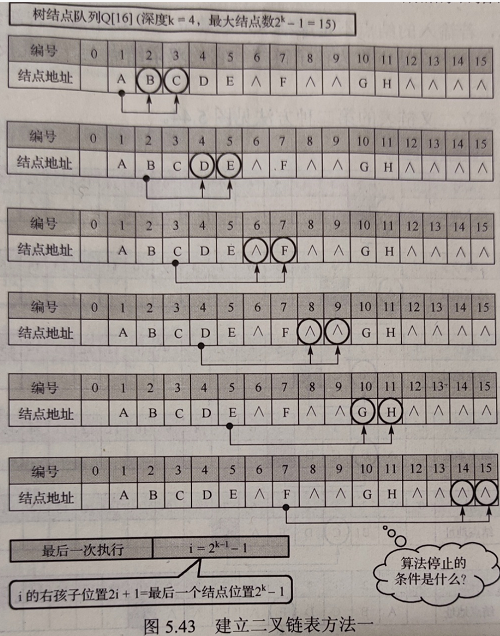
在这里插入图片描述

cpp

cpp实现思路是和python一样的
因为我们在一个节点存储的信息会很多，所以我们构建了一个数据结构treeNodeData
为了保持输入的数据的一致性，所以我们构建了数据结构levelData


#include <iostream>
#include <string>
#include <typeinfo>
#include <queue>
#include <cmath>

using namespace std;

struct treeNodeData{
string name;
int value;
treeNodeData(const string _name, int _value){
    name=_name;
    value=_value;
};
void String(){
    cout << "name: " << name << " value: " << value << endl;
}
};

template<typename T>
struct treeNode{
T data;
treeNode<T>* left;
treeNode<T>* right;
treeNode(T const data=NULL):data(data){
    left=nullptr;
    right=nullptr;
}
};

template<typename T>
void LDR(treeNode<T> *tree);
template<typename T>
void LRD(treeNode<T> *tree);
template<typename T>
void DLR(treeNode<T> *tree);

/*
基于层次输入构建树
*/
struct levelData{
    int max_depth;
    string* name_q;
    int* value_q;
};

treeNode<treeNodeData>* createBiTree(levelData d, treeNode<treeNodeData> *Q[]){
    int last_idx = pow(2, d.max_depth-1) - 1;
    int final_idx = pow(2, d.max_depth) - 1;
    int maxDepth = d.max_depth;
    bool vis_q[final_idx];
    cout << "max_depth: "<< d.max_depth << ", last_idx: " << last_idx << endl;
    cout << final_idx << endl;
    
    fill(vis_q, vis_q+final_idx, false);
    for (int i = 1; i <= last_idx; i++){
        int root_idx = i-1;
        if (d.name_q[root_idx] == "^"){continue;}
        if(!vis_q[root_idx]){// 对于访问过的节点不重新赋值
            treeNodeData *root_data = new treeNodeData(d.name_q[root_idx], d.value_q[root_idx]);
            Q[root_idx] = new treeNode<treeNodeData>(*root_data);
            vis_q[root_idx] = true;
        }

        int left_idx = 2*i-1;
        if (d.name_q[left_idx] == "^"){continue;}
        if(!vis_q[left_idx]){// 对于访问过的节点不重新赋值
            treeNodeData *left_data = new treeNodeData(d.name_q[left_idx], d.value_q[left_idx]);
            Q[left_idx] = new treeNode<treeNodeData>(*left_data);
            vis_q[left_idx] = true;
        }
        Q[root_idx] -> left = Q[left_idx];

        cout << Q[root_idx] -> data.name<< " left->" << Q[left_idx] -> data.name<< endl;

        int right_idx = 2*i+1-1;
        if (d.name_q[right_idx] == "^"){continue;}
        if(!vis_q[right_idx]){
            treeNodeData *right_data = new treeNodeData(d.name_q[right_idx], d.value_q[right_idx]);
            Q[right_idx] = new treeNode<treeNodeData>(*right_data);
            vis_q[right_idx] = true;
        }
        Q[root_idx] -> right = Q[right_idx];

    }
    return Q[0];
}



int main(){
    string name_q[7] = {"aa", "bb", "cc", "dd", "ee", "ff", "^"};
    int value_q[7] = {1, 2, 3, 4, 5, 6, 0};
    int max_depth=floor(log2(7)) +1;
    levelData d = levelData();
    d.max_depth = max_depth;
    d.name_q = name_q;
    d.value_q = value_q;
    treeNode<treeNodeData> *Q[7];
    treeNode<treeNodeData> *bi_tree = createBiTree(d, Q);
    LDR(bi_tree);
    int *qq[5];
    for (int i=1; i<5;i++){
        *qq[i] = i;
        int left_idx = 2 * i;
        if (left_idx > 5){continue;}
        *qq[left_idx] = left_idx;
        *qq[i] = *qq[left_idx];
    }
}




template<typename T>
void LDR(treeNode<T> *tree){
    if(tree->left){
        LDR(tree->left);
    }
    cout << "name: " << tree->data.name << " Value: " << tree->data.value << endl;
    if(tree->right){
        LDR(tree->right);
    }
}

max_depth: 3, last_idx: 3
7
aa left->bb
bb left->dd
cc left->ff
name: bb Value: 2
name: aa Value: 1
name: cc Value: 3

python

class treeNodeData:
    def __init__(self, name, value):
        self.name = name
        self.value = value

    def __str__(self):
        return f'Data[name: {self.name}, value:{self.value}]'

    def __repr__(self):
        return str(self)
    

def creatBiTree(name_list, value_list):
    final_idx = len(name_list)
    Q = [0] * final_idx
    max_depth = math.floor(math.log2(final_idx)) + 1
    last_idx = int(math.pow(2, max_depth-1))
    vis_q = [False] * final_idx
    print(f'max_depth={max_depth}, final_idx={final_idx},last_idx={last_idx} ')
    for idx in range(1, last_idx):
        root_idx = idx - 1
        if name_list[root_idx] == '^': continue;
        if not vis_q[root_idx]:
            root_data = treeNode(data=treeNodeData(
                name_list[root_idx], value_list[root_idx], 
            ))
            Q[root_idx] = root_data
            vis_q[root_idx] = True

        left_idx = 2 * idx - 1
        if name_list[left_idx] == '^': continue;
        if not vis_q[left_idx]:
            left_data = treeNode(data=treeNodeData(
                name_list[left_idx], value_list[left_idx], 
            ))
            Q[left_idx] = left_data
            vis_q[left_idx] = True
    
        Q[root_idx].left = Q[left_idx]

        right_idx = 2 * idx + 1 - 1
        if name_list[right_idx] == '^': continue;
        if not vis_q[right_idx]:
            right_data = treeNode(data=treeNodeData(
                name_list[right_idx], value_list[right_idx], 
            ))
            Q[right_idx] = right_data
            vis_q[right_idx] = True
    
        Q[root_idx].right = Q[right_idx]
    return Q[0]


def ldr_view(tree):
    if tree.left:
        ldr_view(tree.left)
    print(tree.data)
    if tree.right:
        ldr_view(tree.right)
    return None

name_q = "aa bb cc dd ee ff ^".split(' ')
value_q = [1, 2, 3, 4, 5, 6, 0]
tree =  creatBiTree(name_q, value_q)
ldr_view(tree)

>>> tree =  creatBiTree(name_q, value_q)       
max_depth=3, final_idx=7,last_idx=4
>>> ldr_view(tree)
Data[name: dd, value:4]
Data[name: bb, value:2]
Data[name: ee, value:5]
Data[name: aa, value:1]
Data[name: ff, value:6]
Data[name: cc, value:3]

3.2 树遍历

这个就是一个非常典型的递归问题了

cpp

template<typename T>
void LDR(TreeNode<T> *tree){
    if(tree->left){
        LDR(tree->left);
    }
    cout << "name: " << tree->data.name << " Value: " << tree->data.value << endl;
    if(tree->right){
        LDR(tree->right);
    }
}

template<typename T>
void LRD(TreeNode<T> *tree){
    if(tree->left){
        LRD(tree->left);
    }
    if(tree->right){
        LRD(tree->right);
    }
    cout << "name: " << tree->data.name << " Value: " << tree->data.value << endl;
}

template<typename T>
void DLR(TreeNode<T> *tree){
    cout << "name: " << tree->data.name << " Value: " << tree->data.value << endl;
    if(tree->left){
        DLR(tree->left);
    }
    if(tree->right){
        DLR(tree->right);
    }
}

python

# 中序
def ldr_view(tree, out=[]):
    print(out)
    if tree.left:
        ldr_view(tree.left, out)
    
    out.append(tree.data)
    if tree.right:
        ldr_view(tree.right, out)
    return out

ldr_view(tree, out=[])

# 前序
def dlr_view(tree, out=[]):
    out.append(tree.data)
    print(out)
    if tree.left:
        dlr_view(tree.left, out)
    
    if tree.right:
        dlr_view(tree.right, out)
    return out

dlr_view(tree, out=[])


# 后序
def lrd_view(tree, out=[]):
    print(out)
    if tree.left:
        lrd_view(tree.left, out)
    
    if tree.right:
        lrd_view(tree.right, out)
    
    out.append(tree.data)
    return out

lrd_view(tree, out=[])

参考

  • 《数据结构与算法分析新视角》

最后

以上就是迅速毛豆为你收集整理的数据结构_二叉树_属性-构建-遍历一、二叉树的属性二、二叉树的树节点三、二叉树构建与遍历参考的全部内容，希望文章能够帮你解决数据结构_二叉树_属性-构建-遍历一、二叉树的属性二、二叉树的树节点三、二叉树构建与遍历参考所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(47)

相关文章

面试大总结：Java搞定面试中的二叉树题目
面试大总结：Java搞定面试中的二叉树题目
408数据结构学习笔记-树-①树的逻辑结构①定义②结点间的关系描述③结点路径④结点，树的属性描述⑤有序树和无序树⑥森林⑦树的性质（6个性质）
408数据结构学习笔记-树-①树的逻辑结构①定义②结点间的关系描述③结点路径④结点，树的属性描述⑤有序树和无序树⑥森林⑦树的性质（6个性质）
数据结构-难点突破（线索化二叉树与遍历 C++中序线索化二叉树，前序线索二叉树，后序线索二叉树）1. 中序线索化二叉树2. 前序线索二叉树3. 后序线索二叉树
数据结构-难点突破（线索化二叉树与遍历 C++中序线索化二叉树，前序线索二叉树，后序线索二叉树）1. 中序线索化二叉树2. 前序线索二叉树3. 后序线索二叉树
（数据结构）已知二叉树的序列求它的形状（用java实现）
（数据结构）已知二叉树的序列求它的形状（用java实现）
数据结构_二叉树_属性-构建-遍历一、二叉树的属性二、二叉树的树节点三、二叉树构建与遍历参考
数据结构_二叉树_属性-构建-遍历一、二叉树的属性二、二叉树的树节点三、二叉树构建与遍历参考
统计叶子结点 21一、题目描述二、解题思路三、完整代码
统计叶子结点 21一、题目描述二、解题思路三、完整代码
结点逻辑关系任意的非线性结构——图01
结点逻辑关系任意的非线性结构——图01
二叉树[完全二叉树堆的实现]
二叉树[完全二叉树堆的实现]

评论列表共有 0 条评论

立即
投稿
返回
顶部