（数据结构）已知二叉树的序列求它的形状（用java实现）

124 阅读 0 评论 82 点赞

我是靠谱客的博主缓慢超短裙，最近开发中收集的这篇文章主要介绍（数据结构）已知二叉树的序列求它的形状（用java实现），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

已知二叉树的序列求它的形状：有三种方法：

1.根据前序+中序可以求出
2.根据中序+后序可以求出
3.只利用“前序”构建二叉树

方法一：根据前序+中序可以求出

思想：0）一定要先判断长度是否为0

1）前序遍历的第一个元素为二叉树的根结点，再在中序遍历中找根节点的位置leftCount

2）在前序遍历中根节点左边的的数组范围为：[1,leftCount+1);

在中序遍历中根节点左边的的数组范围为：[0,leftCount);

在前序遍历中根节点右边的的数组范围为：[leftCount+1,preorder.length);

在中序遍历中根节点右边的的数组范围为：[leftCount+1,inorder.lenght);

3)重新定义Node结点的头结点，left进行递归，preorder为前面数组中前序的左边，inorder为前面数组中中序的左边，进行递归查找元素，right进行递归，preorder为前面数组中前序的右边，inorder为前面数组中中序的右边，进行递归；

4）返回

例子：

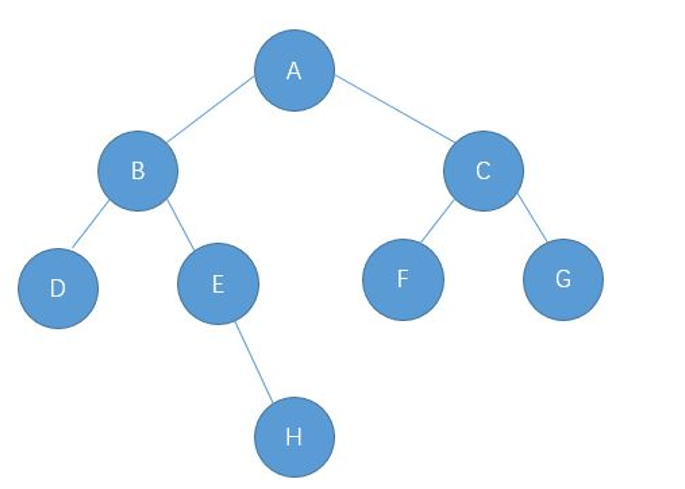
前序遍历为：ABDEHCFG 中序遍历为：DBEHAFCG

代码如下：

//根据先序+中序数组确定二叉树（利用数组）
    public static Node  buildTree1(char [] preorder,char [] inorder) {
        if(preorder.length==0){
            return null;
        }
        char rootValue=preorder[0];
        int leftCount=0;
        for(int i=0;i<inorder.length;i++){
            if(inorder[i]==rootValue){
                leftCount=i;
            }
        }
        char [] leftPreorder= Arrays.copyOfRange(preorder,1,leftCount+1);
        char [] leftInorder=Arrays.copyOfRange(inorder,0,leftCount);
        char [] rightPreorder=Arrays.copyOfRange(preorder,leftCount+1,preorder.length);
        char [] rightInorder=Arrays.copyOfRange(inorder,leftCount+1,inorder.length);
        Node root=new Node(rootValue);
        Node left=buildTree1(leftPreorder,leftInorder);
        Node right=buildTree1(rightPreorder,rightInorder);
        root.left=left;
        root.right=right;
        return root;
    }

方法二：根据中序+后序可以求出

思想：0）一定要先判断长度是否为0

1）后序遍历的最后一个元素为二叉树的根结点，再在中序遍历中找根节点的位置leftCount

2）在中序遍历中根节点左边的的数组范围为：[0,leftCount);

在后序遍历中根节点左边的的数组范围为：[0,leftCount);

在中序遍历中根节点右边的的数组范围为：[leftCount+1,inorder.lenght);

在后序遍历中根节点右边的的数组范围为：[leftCount，postorder.length-1);

3)重新定义Node结点的头结点，left进行递归，inorder为前面数组中中序的左边，postorder为前面数组中后序的左边，进行递归查找元素，right进行递归，inorder为前面数组中中序的右边，postorder为前面数组中后序的右边，进行递归；

4）返回

例子：

中序遍历：DBEHAFCG 后序遍历：DHEBFGCA

代码如下：

//根据中序+后序确定二叉树（数组）
    public static Node buildTree2(char [] inorder,char [] postorder){
        if(inorder.length==0){
            return null;
        }
        char rootValue=postorder[postorder.length-1];
        int leftCount=0;
        for(int i=0;i<inorder.length;i++){
            if(inorder[i]==rootValue){
                leftCount=i;
            }
        }
        char [] leftInorder=Arrays.copyOfRange(inorder,0,leftCount);
        char [] leftPostorder=Arrays.copyOfRange(postorder,0,leftCount);
        char [] rightInorder=Arrays.copyOfRange(inorder,leftCount+1,inorder.length);
        char [] rightPostorder=Arrays.copyOfRange(postorder,leftCount,postorder.length-1);
        Node root=new Node(rootValue);
        Node left=buildTree2(leftInorder,leftPostorder);
        Node right=buildTree2(rightInorder,rightPostorder);
        root.left=left;
        root.right=right;
        return root;
    }

方法三：只利用“前序”构建二叉树

思想：在前序遍历中，没有结点的位置要用'#'代替

1)ReturnValue职责：用root构造出一棵树，使用Node结点，用used确定使用过的值

2）先判断长度是否为空

3）先序的第一个结点为结点，rootValue

4）判断节点是否为'#'，如果是的话，root为null,used加1；

5）利用找先序中的左边和右边

6）最后确定root结点的left、right

//只利用“前序”构建二叉树
    public static class ReturnValue{
        Node root;
        int used;
    }
    public static ReturnValue buildTreePreorder(List<Character> preorder){
        if(preorder.size()==0){
            ReturnValue rv=new ReturnValue();
            rv.root=null;
            rv.used=0;
            return rv;
        }
        char rootValue=preorder.get(0);
        if(rootValue=='#'){
            ReturnValue rv=new ReturnValue();
            rv.root=null;
            rv.used=1;
            return rv;
        }
        ReturnValue leftPreoder=buildTreePreorder(preorder.subList(1,preorder.size()));
        ReturnValue rightPreorder=buildTreePreorder(preorder.subList(1+leftPreoder.used,preorder.size()));
        Node root=new Node(rootValue);
        root.left=leftPreoder.root;
        root.right=rightPreorder.root;
        ReturnValue rv=new ReturnValue();
        rv.root=root;
        rv.used=1+leftPreoder.used+rightPreorder.used;
        return rv;
    }