Java数据结构学习——排序二叉树前言正文总结

68 阅读 0 评论 45 点赞

我是靠谱客的博主香蕉白开水，最近开发中收集的这篇文章主要介绍Java数据结构学习——排序二叉树前言正文总结，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

前言

正文

排序二叉树的特点

插入节点

删除树节点

删除的节点是叶子节点

删除的节点存在左或者右子节点

删除的节点存在左右两子节点

遍历节点

先序遍历

中序遍历

后续遍历

全部代码展示

总结

前言

由于本人的数据结构和算法能力比较薄弱，不管是在面试还是对于代码的一个性能提升都是少不过数据结构和算法的支撑，所以有断断续续的学习，此专栏就记录一下自己的学习过程和成果把！对大家不一定有帮助，更希望如果有错误之处希望能给我提出来！

正文

排序二叉树的特点

一个父节点只能有左右两个子节点。
左节点的值比父节点要小。
右节点的值要比父节点要大。

插入节点

从排序二叉树的特点我们只要一个父节点只能有2个子节点，并且左小右大，所以我们来一串数据可以自己先手动排序理清思路。[6,1,4,2,10,-1,15,8]；

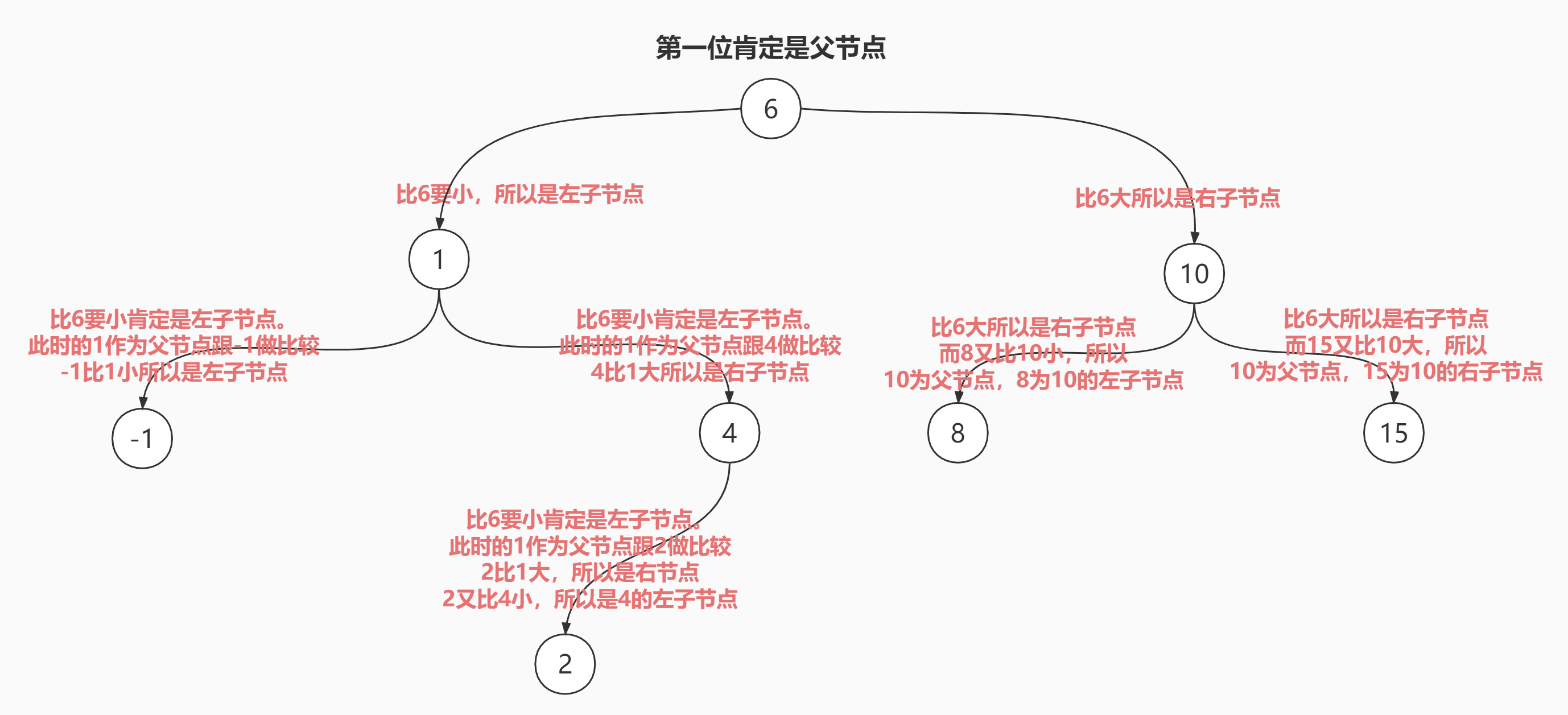
建议大家也写一串数字，然后自己手绘一把理清思绪好为写代码做铺垫

代码如下：

// 根节点
private TreeNode rootNode;

public TreeNode getRootNode() {
    return rootNode;
}

public void insertNode(TreeNode node){

    // 从根节点开始遍历新增的位置，
    // 左右节点有为null的就可以直接插入
    // // 判断根节点是否存在，不存在当前节点就是根节点
    if(rootNode==null){   
        rootNode = node;
        rootNode.setLefe(null);
        rootNode.setRight(null);

    // 这里就是代表根节点存在，就开始往下找
    }else{    

        // 获取到根节点作为循环最开始父节点
        // 后续在循环中一直作为父节点，可变参数
        TreeNode currentNode = rootNode;  
        
        // 循环判断新来的节点是小于还是大于父节点,看怎么走分支
        while(true){

            // 走当前父节点右边
            // 判断条件就是新来的节点的值是否小于当前父节点
            if(node.getValue()< currentNode.getValue()){

                // 为null就直接放
                if(currentNode.getLefe()==null){
                    currentNode.setLefe(node);
                    return;
                }

                // 不为null就代表还有子节点，继续把当前父节点的左节点作为下次循环的父节点
                currentNode = currentNode.getLefe();

            // 走当前父节点的右边
            // 判断条件就是新来的节点的值是否大于当前父节点
            }else if (node.getValue()> currentNode.getValue()){      

                // 为null就直接放
                if(currentNode.getRight()==null){
                    currentNode.setRight(node);
                    return;
                }

                // 不为null就代表还有子节点，继续把当前父节点的右节点作为下次循环的父节点
                currentNode = currentNode.getRight();

            // 大于和小于都判断过了，所以进入到这里就达标重复了
            // 重复的逻辑自己定义，可以使替换之类的...   我这里就不能重复了
            }else{
                System.out.println("当前节点已经存在于树中");
                return;
            }
        }
    }
}


// 树节点的结构
class TreeNode{
    private int value;
    private TreeNode lefe;
    private TreeNode right;


    public TreeNode(int value) {
        this.value = value;
    }

    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    public TreeNode getLefe() {
        return lefe;
    }

    public void setLefe(TreeNode lefe) {
        this.lefe = lefe;
    }

    public TreeNode getRight() {
        return right;
    }

    public void setRight(TreeNode right) {
        this.right = right;
    }
}

详细讲解看代码块的注释，每行的注释都是讲解的特别仔细。

插入的逻辑比较容易，就是新来的节点一直和当前的父节点做大小的比较走不同的分支，直到当前的父节点的左或右的子节点为null就可以直接添加。

删除树节点

对于排序二叉树来说删除节点大致可以分为

删除的节点是叶子节点，也就是删除的节点不存在左右子节点。
删除的节点存在左子节点。
删除的节点存在右子节点。
删除的节点存在左右两子节点。

删除的节点是叶子节点

什么是叶子节点？

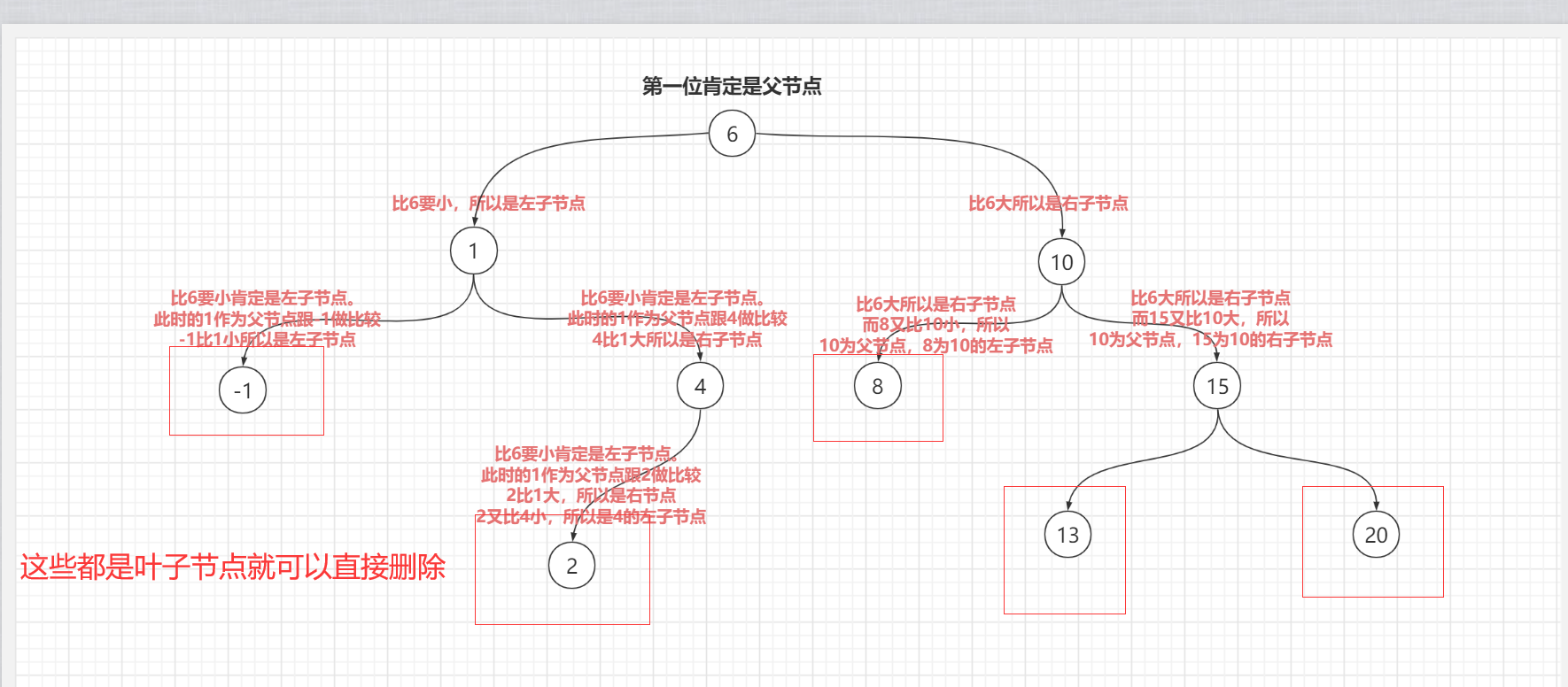
那我们该如何删除呢？

这里我们需要根据value值找到删除的叶子节点和叶子节点的父节点。

为什么要找到父节点呢？因为我们需要通过父节点来找到删除节点是在左边还是右边，并且将删除节点的父节点的left或者right指向为null，help GC来回收删除节点。

帮助删除方法——根据删除的value找到删除的节点

    // 删除方法的帮助方法——根据删除的value查找到删除的节点
    private TreeNode selectNode(int value){

        TreeNode currentNode = rootNode;

        // 如果root节点为null就直接返回null
        // 如果root节点的left和right都为null就直接返回null
        // 冗余代码，因为查询删除节点和查询删除节点的父节点都要查询。可以只在调用的地方使用一次
//        if (currentNode==null) {
//            return null;
//        }

        while(true) {

            if(currentNode.getLefe()==null && currentNode.getRight()==null){
                return null;
            }

            // 如果查找的值小于
            if(currentNode.getLefe()!=null && value < currentNode.getValue()) {

                if(currentNode.getLefe().getValue()==value){
                    return currentNode.getLefe();
                }
                currentNode = currentNode.getLefe();

            }else if(currentNode.getRight()!=null&& value>currentNode.getValue()){          // 如果查找的值大于

                if(currentNode.getRight().getValue()==value){
                    return currentNode.getRight();
                }
                currentNode = currentNode.getRight();
            }
        }
    }

帮助删除方法——根据删除的value找到删除节点的父节点


 // 删除方法的帮助方法——根据删除的value查找到删除的节点的父节点
    private TreeNode selectParentNode(int value) {

        TreeNode currentNode = rootNode;

        // rootNode判空代码在调用此方法之前要做，这里不用判断可以避免没必要的冗余

        // 这种情况就是只有rootNode节点。
        if(currentNode.getLefe()==null && currentNode.getRight()==null){
            return currentNode;
        }

        while (true){
            // 不用考虑线程安全的问题的话
            // 先调用查找删除节点的方法就保证了有父节点，所以这里对节点的判空也可以避免
            if(currentNode.getLefe()!=null && value<currentNode.getValue()){
                if (currentNode.getLefe().getValue()==value) {
                    // 这里是返回父节点
                    return currentNode;
                }
                currentNode = currentNode.getLefe();
            }else if (currentNode.getRight()!=null && value>currentNode.getValue()){
                if (currentNode.getRight().getValue()==value) {
                    // 这里是返回父节点
                    return currentNode;
                }
                currentNode = currentNode.getRight();
            }
        }
    }

具体的删除代码在后面的删除的节点存在左右两字节点

删除的节点存在左或者右子节点

这种删除，我们就直接让左或者右子节点来代替删除节点就行了。

但是我们要考虑是左还是又子节点，并且还是考虑删除节点是在父节点的左子节点还是右子节点

具体的删除代码在后面的删除的节点存在左右两字节点

删除的节点存在左右两子节点

这种就比较复杂了，因为左右子节点都存在，这种情况，我们就要把当前删除节点的右子节点当做一个树，找到树中最小的节点，也就是最左边节点。找到后我们需要把最小节点来代替删除节点。并且这种情况也存在删除的右子节点的左子节点不存在，这种情况就直接把删除的右子节点来代替删除的节点，所以我们需要找到右子节点中最小节点和最小节点的父节点，找父节点的方法前面已经展示了。

帮助删除方法——根据删除的value找到删除节点的父节点

    // 帮助删除——删除节点存在两个左右子节点的情况
    // 找右子树的最小节点
    private TreeNode selectRightMinimum(TreeNode node){


        TreeNode mixLeft = node.getRight().getLefe();

        // 冗余代码，此代码应该是调用此方法者处理。
//        if(mixLeft ==null){
//            return node.getRight();
//        }

        while(true){

            if(mixLeft.getLefe()==null){
                return mixLeft;
            }
            mixLeft = mixLeft.getLefe();
        }
    }

所以整体的删除代码如下：

    // 删除节点
    public void deleteNode(int value){

        // 因为selectNode和selectParentNode没有对root节点做判断，所以这里做，也减少了代码的冗余
        if(rootNode==null){
            System.out.println("删除失败，树还没任何节点");
            return;
        }

        // 这个代表只有根节点
        if (rootNode.getValue()==value && rootNode.getRight()==null && rootNode.getLefe()==null) {

            // 直接把根节点
            rootNode = null;
            return;
        }

        TreeNode targetNode = this.selectNode(value);

        // 这个代表删除的值在树中没得
        if (targetNode== null) {
            System.out.println("您删除的内容树中没有");
            return;
        }

        // 获取到删除节点的父节点，因为要靠他找到删除节点是左边还是右边，并且帮助GC回收删除节点
        TreeNode parentNode = this.selectParentNode(value);


        // 下面就是删除的具体逻辑代码了
        // 这里需要分情况讨论了
        // 可能是叶子节点，就直接把当前节点给删除，其他操作都不需要做
        if(targetNode.getLefe()==null && targetNode.getRight()==null){

            // 但是我们并不知道targetNode是parentNode的左还是右子节点，所以需要if判断
            if(parentNode.getLefe().getValue()==value){
                parentNode.setLefe(null);
            }else{
                parentNode.setRight(null);
            }

        // 这种情况就是处理删除节点存在左子节点，右子节点不存在
        // 但是我们并不知道删除节点是在父节点的左边还是右边， 所以下面还有对方法做判断
        }else if(targetNode.getLefe()!=null && targetNode.getRight()==null){

            // 删除节点在parent节点的左边
            if(parentNode.getLefe().getValue()==value){

                // 将删除节点的左边节点赋值给父节点的左边节点
                parentNode.setLefe(targetNode.getLefe());

              
            }else{  // 这里代表删除节点在父节点的右边    
                
                // 将删除节点的左边节点赋值给父节点的左边节点
                parentNode.setRight(targetNode.getLefe());
            }


        // 这种情况就是处理删除节点存在右子节点，左子节点不存在
        // 但是我们并不知道删除节点是在父节点的左边还是右边， 所以下面还有对方法做判断
        }else if(targetNode.getLefe()==null && targetNode.getRight()!=null){

            // 删除节点在parent节点的左边
            if(parentNode.getLefe().getValue()==value){
                parentNode.setLefe(targetNode.getRight());
            }else{       // 删除节点在parent节点的右边
                parentNode.setRight(targetNode.getRight());
            }

        // 这种情况代表删除节点同时存在左右子节点
        }else{          

            // 这里代表右边节点作为树不存在左节点，所以直接处理右节点，
            // 也就是右节点树最小的就是右边第一个节点
            if (targetNode.getRight().getLefe()==null) {

                // 将删除节点的父节点的指向改变
                parentNode.setRight(targetNode.getRight());

                // 这里的getRight()获取到的节点就是删除节点的右子节点了
                parentNode.getRight().setLefe(targetNode.getLefe());
                return;
            }

            // 执行到这里就代表删除节点的右子节树存在左子节点
            // 所以我们就要通过我们前面编写好的帮助方法找到最小值
            // 改变指向的代码我就不注释了，这个大家要根据自己手绘图自己思考。
            TreeNode minimumNode = this.selectRightMinimum(targetNode);
            TreeNode minimumNodeParent = this.selectParentNode(minimumNode.getValue());
            minimumNodeParent.setLefe(null);  // help GC
            parentNode.setRight(minimumNode);
            parentNode.getRight().setLefe(targetNode.getLefe());
            parentNode.getRight().setRight(targetNode.getRight());
        }

    }

上面代码块的注释已经特别的仔细了，不过这里建议大家根据博主的代码+自己手绘图来逐行理解

方法的前半段我们做一些特殊的判断，之后就根据删除节点的子节点做一些判断并做出不同的操作

遍历节点

对于排序二叉树来说，遍历分为三种遍历。

先序：根->左->右

中序：左->根->右

后续：左-> 右 ->根

先序遍历

// 亲忽略我的中文式命名（如果不是英文差，谁又愿意呢...）
// 根->左->又
public void xianXu(TreeNode treeNode){

    // 递归的退出条件
    if(treeNode!=null){

        System.out.print(treeNode.getValue()+"tt");

        // 左边
        xianXu(treeNode.getLefe());

        // 右边
        xianXu(treeNode.getRight());
    }
}

对于递归的操作也不是文字能描述明白的，更多的是大家根据代码和输出结构再根据自己手绘的图来做一个理解，不过我这里还是画个图来给大家理解一下吧。

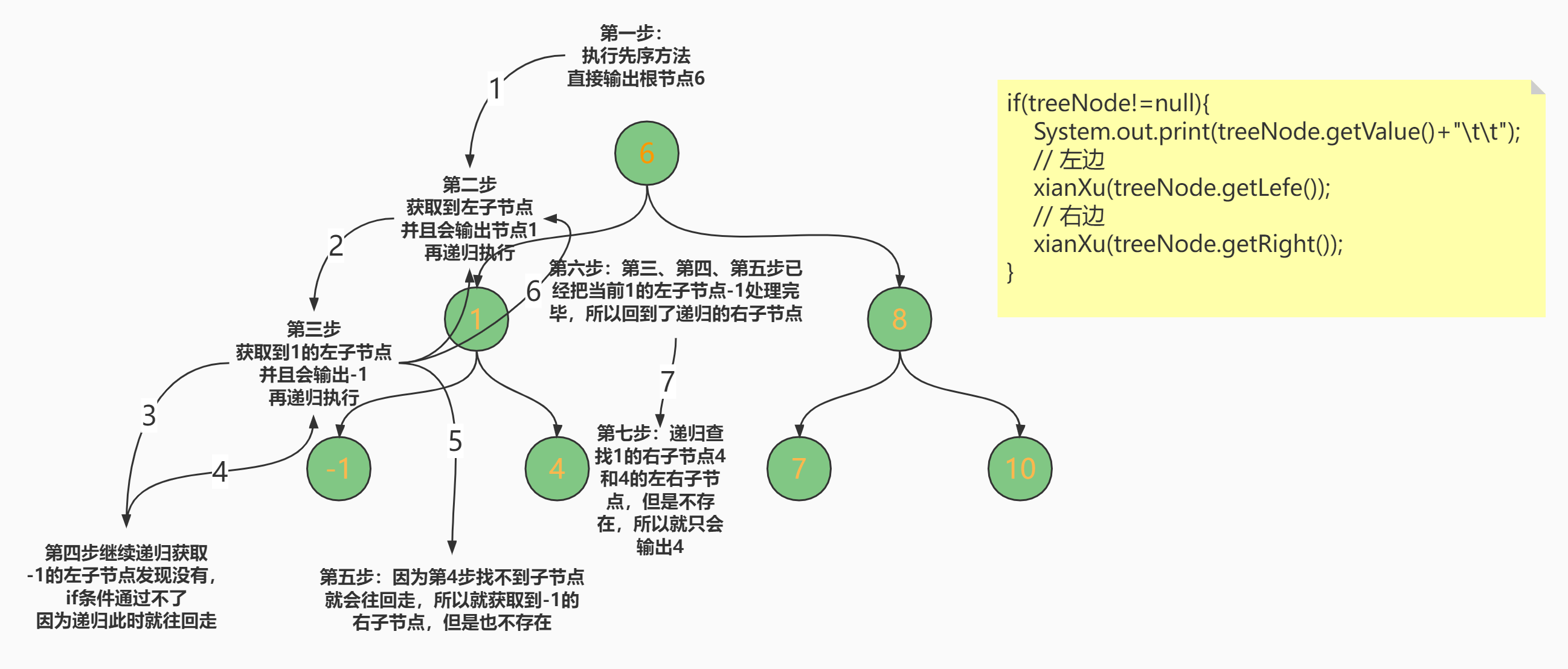
注：如果图理解起来比较晕看不懂的话，就自己画图，因为每个人的思想和思路不一样，不要被我的图打乱思绪

中序遍历

// 左->根->右
public void zhongXu(TreeNode treeNode){

    if(treeNode!=null){

        zhongXu(treeNode.getLefe());
        System.out.print(treeNode.getValue()+"tt");
        zhongXu(treeNode.getRight());
    }
}

如果理解了先序遍历的思路，这里也不需要任何解释，一个递归的先后顺序变了，但是有没有发现中序遍历时从小到大的。建议大家使用手绘图来理解递归！

后续遍历

// 左-> 右 ->根
public void houXu(TreeNode treeNode){

    if(treeNode!=null){

        zhongXu(treeNode.getLefe());
        zhongXu(treeNode.getRight());
        System.out.print(treeNode.getValue()+"tt");
    }
}

如果理解了先序遍历的思路，这里也不需要任何解释，就是递归的先后顺序变了。建议大家使用手绘图来理解递归！

全部代码展示

package tree.erchaTree;

import sun.reflect.generics.tree.Tree;

/**
 * @author liha
 * @version 1.0
 * @date 2022/3/8 11:18
 */
public class BinaryTree {

    // 根节点
    private TreeNode rootNode;

    public TreeNode getRootNode() {
        return rootNode;
    }

    @Override
    public String toString() {
        return "BinaryTree{" +
                "rootNode=" + rootNode +
                '}';
    }


    /**
     *@description 新增节点

     *@params
     * @param node

     *@return

     *@create_time  2022/3/8 11:25
     *@update_time  2022/3/8 11:25
     */
    public void insertNode(TreeNode node){

        // 从根节点开始遍历新增的位置，并且左右节点有为null的就可以直接插入
        if(rootNode==null){   // 判断根节点是否存在，不存在当前节点就是根节点

            rootNode = node;
            rootNode.setLefe(null);
            rootNode.setRight(null);
        }else{    // 这里就是代表根节点存在，就开始往下找

            TreeNode currentNode = rootNode;  // 最开始获取到根节点

            // 循环判断新来的节点是小于还是大于当前节点,看怎么走分支
            while(true){
                // 走左边
                if(node.getValue()< currentNode.getValue()){
                    // 为null就直接放
                    if(currentNode.getLefe()==null){
                        currentNode.setLefe(node);
                        return;
                    }

                    currentNode = currentNode.getLefe();
                }else if (node.getValue()> currentNode.getValue()){      // 走右边

                    // 为null就直接放
                    if(currentNode.getRight()==null){
                        currentNode.setRight(node);
                        return;
                    }
                    // 不为null就赋值继续自旋
                    currentNode = currentNode.getRight();
                }else{
                    System.out.println("当前节点已经存在于树中");
                    return;
                }
            }
        }
    }

    // 删除节点
    public void deleteNode(int value){

        // 因为selectNode和selectParentNode没有对root节点做判断，所以这里做，也减少了代码的冗余
        if(rootNode==null){
            System.out.println("删除失败，树还没任何节点");
            return;
        }

        // 这个代表只有根节点
        if (rootNode.getValue()==value && rootNode.getRight()==null && rootNode.getLefe()==null) {

            // 直接把根节点
            rootNode = null;
            return;
        }

        TreeNode targetNode = this.selectNode(value);

        // 这个代表删除的值在树中没得
        if (targetNode== null) {
            System.out.println("您删除的内容树中没有");
            return;
        }

        TreeNode parentNode = this.selectParentNode(value);


        // 这里需要分情况讨论了
        // 可能是叶子节点，就直接把当前节点给删除，其他操作都不需要做
        if(targetNode.getLefe()==null && targetNode.getRight()==null){
            // 但是我们并不知道targetNode是parentNode的左还是右子节点，所以需要if判断
            if(parentNode.getLefe().getValue()==value){
                parentNode.setLefe(null);
            }else{
                parentNode.setRight(null);
            }
        }else if(targetNode.getLefe()!=null && targetNode.getRight()==null){

            // 删除节点在parent节点的左边
            if(parentNode.getLefe().getValue()==value){
                parentNode.setLefe(targetNode.getLefe());
            }else{       // 删除节点在parent节点的右边
                parentNode.setRight(targetNode.getLefe());
            }

        }else if(targetNode.getLefe()==null && targetNode.getRight()!=null){

            // 删除节点在parent节点的左边
            if(parentNode.getLefe().getValue()==value){
                parentNode.setLefe(targetNode.getRight());
            }else{       // 删除节点在parent节点的右边
                parentNode.setRight(targetNode.getRight());
            }

        }else{          // 删除存在两个节点

            // 这里代表右边树不存在左节点，所以直接处理右节点，也就是右树最小的就是右边第一个父节点
            if (targetNode.getRight().getLefe()==null) {


                parentNode.setRight(targetNode.getRight());
                parentNode.getRight().setLefe(targetNode.getLefe());
                return;
            }

            // 执行到这里代表target节点子树存在左边最小值。
            // 就找到最小值
            TreeNode minimumNode = this.selectRightMinimum(targetNode);
            TreeNode minimumNodeParent = this.selectParentNode(minimumNode.getValue());
            minimumNodeParent.setLefe(null);  // help GC
            parentNode.setRight(minimumNode);
            parentNode.getRight().setLefe(targetNode.getLefe());
            parentNode.getRight().setRight(targetNode.getRight());
        }

    }

    // 帮助删除——删除节点存在两个左右子节点的情况
    // 找右子树的最小节点
    private TreeNode selectRightMinimum(TreeNode node){


        TreeNode mixLeft = node.getRight().getLefe();

        // 冗余代码，调用此方法者处理。
//        if(mixLeft ==null){
//            return node.getRight();
//        }

        while(true){

            if(mixLeft.getLefe()==null){
                return mixLeft;
            }
            mixLeft = mixLeft.getLefe();
        }
    }

    // 删除方法的帮助方法——根据删除的value查找到删除的节点
    private TreeNode selectNode(int value){

        TreeNode currentNode = rootNode;

        // 如果root节点为null就直接返回null
        // 如果root节点的left和right都为null就直接返回null
        // 冗余代码，因为查询删除节点和查询删除节点的父节点都要查询。可以只在调用的地方使用一次
//        if (currentNode==null) {
//            return null;
//        }

        while(true) {

            if(currentNode.getLefe()==null && currentNode.getRight()==null){
                return null;
            }

            // 如果查找的值小于
            if(currentNode.getLefe()!=null && value < currentNode.getValue()) {

                if(currentNode.getLefe().getValue()==value){
                    return currentNode.getLefe();
                }
                currentNode = currentNode.getLefe();

            }else if(currentNode.getRight()!=null&& value>currentNode.getValue()){          // 如果查找的值大于

                if(currentNode.getRight().getValue()==value){
                    return currentNode.getRight();
                }
                currentNode = currentNode.getRight();
            }
        }
    }

    // 删除方法的帮助方法——根据删除的value查找到删除的节点的父节点
    private TreeNode selectParentNode(int value) {

        TreeNode currentNode = rootNode;

        // rootNode判空代码在调用此方法之前要做，这里不用判断可以避免没必要的冗余

        // 这种情况就是只有rootNode节点。
        if(currentNode.getLefe()==null && currentNode.getRight()==null){
            return currentNode;
        }

        while (true){
            // 不用考虑线程安全的问题的话
            // 先调用查找删除节点的方法就保证了有父节点，所以这里对节点的判空也可以避免
            if(currentNode.getLefe()!=null && value<currentNode.getValue()){
                if (currentNode.getLefe().getValue()==value) {
                    // 这里是返回父节点
                    return currentNode;
                }
                currentNode = currentNode.getLefe();
            }else if (currentNode.getRight()!=null && value>currentNode.getValue()){
                if (currentNode.getRight().getValue()==value) {
                    // 这里是返回父节点
                    return currentNode;
                }
                currentNode = currentNode.getRight();
            }
        }
    }



    // 遍历的几种方式
    // 根->左->右
    // 左->根->右
    // 左->右->根

    // 根->左->又
    public void xianXu(TreeNode treeNode){

        // 递归的退出条件
        if(treeNode!=null){

            System.out.print(treeNode.getValue()+"tt");

            // 左边
            xianXu(treeNode.getLefe());

            // 右边
            xianXu(treeNode.getRight());
        }
    }


    // 左->根->右
    public void zhongXu(TreeNode treeNode){

        if(treeNode!=null){

            zhongXu(treeNode.getLefe());
            System.out.print(treeNode.getValue()+"tt");
            zhongXu(treeNode.getRight());
        }
    }


    // 左-> 右 ->根
    public void houXu(TreeNode treeNode){

        if(treeNode!=null){

            zhongXu(treeNode.getLefe());
            zhongXu(treeNode.getRight());
            System.out.print(treeNode.getValue()+"tt");
        }
    }



}

class TreeNode{
    private int value;
    private TreeNode lefe;
    private TreeNode right;


    public TreeNode(int value) {
        this.value = value;
    }

    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    public TreeNode getLefe() {
        return lefe;
    }

    public void setLefe(TreeNode lefe) {
        this.lefe = lefe;
    }

    public TreeNode getRight() {
        return right;
    }

    public void setRight(TreeNode right) {
        this.right = right;
    }
}

测试代码

/**
 * @author liha
 * @version 1.0
 * @date 2022/3/8 14:24
 */
public class Test {

    public static void main(String[] args) {


        BinaryTree tree = new BinaryTree();

        tree.insertNode(new TreeNode(6));
        tree.insertNode(new TreeNode(1));
        tree.insertNode(new TreeNode(4));
        tree.insertNode(new TreeNode(2));
        tree.insertNode(new TreeNode(10));
        tree.insertNode(new TreeNode(-1));
        tree.insertNode(new TreeNode(15));
        tree.insertNode(new TreeNode(8));
        tree.insertNode(new TreeNode(13));
        tree.insertNode(new TreeNode(20));


        tree.zhongXu(tree.getRootNode());

        tree.deleteNode(10);

        System.out.println("删除过后");

        tree.zhongXu(tree.getRootNode());

    }
}

总结

难度并不大，但是得花时间画图来理解。

最后如果此贴有帮助到您，希望能点赞+关注，您的支持是我最大的努力！~

最后

以上就是香蕉白开水为你收集整理的Java数据结构学习——排序二叉树前言正文总结的全部内容，希望文章能够帮你解决Java数据结构学习——排序二叉树前言正文总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：数据结构与算法的学习
浏览次数：68 次浏览
发布日期：2024-05-15 00:30:01
本文链接：https://www.kaopuke.com/article/k-p-k_13_u_7_o_26_f0_13__23__26_4.html

Java数据结构学习——排序二叉树前言正文总结

概述

前言

正文

排序二叉树的特点

插入节点

删除树节点

删除的节点是叶子节点

删除的节点存在左或者右子节点

删除的节点存在左右两子节点

遍历节点

先序遍历

中序遍历

后续遍历

全部代码展示

总结

最后

评论列表共有 0 条评论

发表评论取消回复

Java数据结构学习——排序二叉树前言正文总结

概述

前言

正文

排序二叉树的特点

插入节点

删除树节点

删除的节点是叶子节点

删除的节点存在左或者右子节点

删除的节点存在左右两子节点

遍历节点

先序遍历

中序遍历

后续遍历

全部代码展示

总结

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

发表评论取消回复