算法-“之”字形打印矩阵

题目

给定一个矩阵matrix，按照“之”字形的方式打印这个矩阵，要求额外空间复杂度为O(1)。
例如： 1，2，3，4，5，6，7，8，9，10，11，12
“之”字形打印的结果为：1，2，5，9，6，3，4，7，10，11，8，12

思路
基本题意为按照当前图示打印矩阵

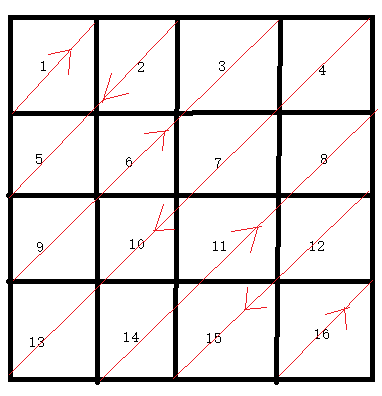
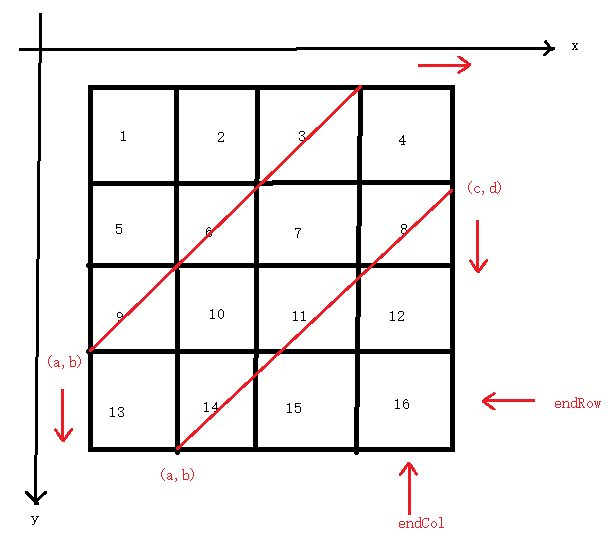
我们只需要确定对角线的顶点即可，假设对角线左下角为(a,b)，右上角为(c,d)，从左上角顶点(0,0)开始两个点同时移动，(a,b)开始向下移动(a++)，遇到下边界endRow之后向右移动(b++)；(c,d)开始向右移动(d++)，遇到右边界之后向下移动(c++)，当两点重合时即结束。

代码

/**
 * “之”字形打印矩阵
 * 【题目】 给定一个矩阵matrix，按照“之”字形的方式打印这个矩阵
 * 例如： 1 2 3 4 5 6 7 8 9 10 11 12 “之”字形打印的结果为：1，2，5，9，6，3，4，7，10，11，8，12
 * 【要求】 额外空间复杂度为O(1)。
 *
 * @Author: FangJu
 * @Date: 2019/8/11
 */
public class ZigZagPrintMatrix {

    public static void main(String[] args) {
        int[][] matrix = {
                {1, 2, 3, 4},
                {5, 6, 7, 8},
                {9, 10, 11, 12},
                {13, 14, 15, 16}
        };
        printMatrixZigZag(matrix);
    }

    /**
     * 打印“之”字形打印矩阵
     *
     * @param matrix 矩阵
     */
    private static void printMatrixZigZag(int[][] matrix) {
        int a = 0;
        int b = 0;
        int c = 0;
        int d = 0;
        int endRow = matrix.length - 1;
        int endCol = matrix[0].length - 1;
        boolean fromUp = true;
        while (b <= endCol) {
            printLevel(matrix, a, b, c, d, fromUp);
            b = (a == endRow) ? b + 1 : b;
            a = (a == endRow) ? a : a + 1;
            c = (d == endCol) ? c + 1 : c;
            d = (d == endCol) ? d : d + 1;
            fromUp = !fromUp;
        }
    }

    /**
     * 打印矩阵对角线
     *
     * @param matrix 矩阵
     * @param a      矩阵左下角行
     * @param b      矩阵左下角列
     * @param c      矩阵右上角行
     * @param d      矩阵右上角列
     * @param flag   从上至下/从下至上(true/false)
     */
    private static void printLevel(int[][] matrix, int a, int b, int c, int d, boolean flag) {
        if (flag) {
            while (c <= a && d >= b) {
                System.out.print(matrix[c++][d--] + "t");
            }
        } else {
            while (a >= c && b <= d) {
                System.out.print(matrix[a--][b++] + "t");
            }
        }
    }

}

最后

以上就是调皮便当为你收集整理的算法-“之”字形打印矩阵的全部内容，希望文章能够帮你解决算法-“之”字形打印矩阵所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。