【算法】【链表模块】两个单链表寻找交点前言问题介绍解决方案代码编写思考感悟写在最后

前言

当前所有算法都使用测试用例运行过，但是不保证100%的测试用例，如果存在问题务必联系批评指正~

在此感谢左大神的书让我对算法有了新的感悟认识！

问题介绍

原问题
给定两个单链表，如果单链表相交，返回交点，否则返回null

解决方案

方案一：
1、分析情况

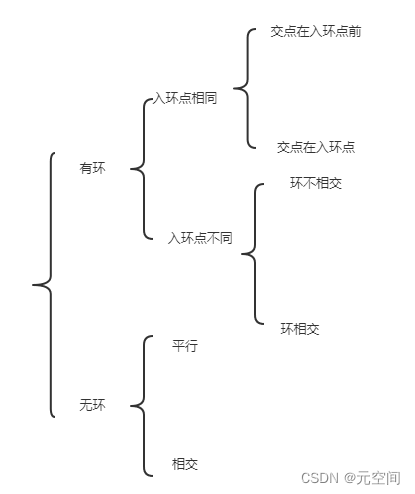
1、一个快节点、一个慢节点，通过是否相遇来判断是否存在环
2、无环情况：
· 取长度，直接找公共点，没有就null
3、有环情况：寻找入环点，请看4
· 入环点相同：入环点在环上和环外都不影响正常的取长度直接寻找公共点的逻辑，只不过遍历结束条件需要注意一下，入环点为结束条件
· 入环点不同：通过一个单链表的遍历是够存在另一个单链表的入环点来判断是否平行
· 平行：null
· 环相交：直接返回任意一个单链表的入环点即可
4、寻找入环点：
快慢节点先从head出发，快节点速度为2，慢节点速度为1
快慢节点一定会相遇，第一次相遇的地方记为a点
此时将快节点指向head，速度调整为1，再次进行两个节点的遍历，一定会第二次相遇，第二次相遇的地方就是入环点。
证明：

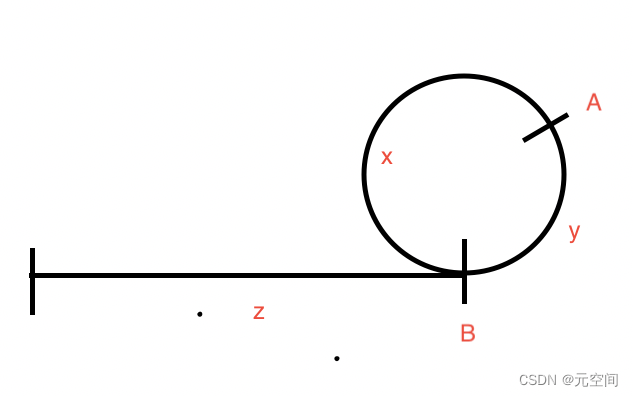
A：第一次相遇点
B：入环点
1、首先在A点可以知道一个公式：
2*[z+n(x+y) + y] = z+m(x+y)+y
其中n为慢节点在环中旋转的圈数，起点为B，m为快节点旋转的圈数，起点也为B，化简后：
z + y = （m-n） * (x+y) …1
说明z+y是整数倍的环长，那么此时慢节点在A点，快节点放到起点，两个点速度都为1时，是否会相遇？
1式：
z = （m-n）(x+y) - y 表示z的长度为：若干圈长度-y，此时假设起点为快节点，快节点（现在速度为1，与慢节点相同）走了（m-n-1）（x+y）的距离后，慢节点应该还是在A点，因为慢节点一直在循环，那么此时快节点距离B点还差x+y-y个距离，也就是x距离了，到这里应该就不用解释了，证明完毕！

代码编写

java语言版本

方案二：

public class JudgeNodeListCross {
    public static LinkNode myGetCross(LinkNode head1, LinkNode head2){
        if (head1 == null || head2 == null){
            return null;
        }
        LinkNode res = null;
        LinkNode loopNode1 = myGetLoopNode(head1);
        LinkNode loopNode2 = myGetLoopNode(head2);
        if (loopNode1 == null && loopNode2 == null){
            res = findCross(head1, head2, null, null);
        }else if (loopNode1 != null && loopNode2 != null){
            // 都成环
            if (loopNode1 == loopNode2){
                // 入环点相同
                res = findCross(head1, head2, loopNode1, loopNode2);
            }else {
                LinkNode cur = head1;
                boolean isFirst = true;
                while (cur != loopNode1 || isFirst){
                    if (cur == loopNode1){
                        isFirst = false;
                    }
                    if (cur == loopNode2){
                        // loop1和2都可以
                        res = loopNode2;
                        break;
                    }
                    cur = cur.getNext();
                }

            }
        }
        return res;
    }


    /**
     * 寻找入环点
     * @param head
     * @return
     */
    private static LinkNode myGetLoopNode(LinkNode head) {
        LinkNode fast = head;
        LinkNode slow = head;
        //一轮
        while (fast != null && fast.getNext() != null){
            fast = fast.getNext().getNext();
            slow = slow.getNext();
            if (fast == slow){
                break;
            }
        }
        fast = head;
        // 二轮
        while (fast != null && slow != null && fast != slow){
            fast = fast.getNext();
            slow = slow.getNext();
        }
        // 这里只能给slow，因为无环单链表的情况下slow先到头
        return slow;
    }

    private static LinkNode findCross(LinkNode head1, LinkNode head2, LinkNode loop1, LinkNode loop2){
        LinkNode res = null;
        // 没有环
        int len1 = CommonUtils.getLinkNodeLenth(head1, loop1);
        int len2 = CommonUtils.getLinkNodeLenth(head2, loop2);
        int abs = Math.abs(len1 - len2);
        LinkNode lenHead = len1 >= len2 ? head1 : head2;
        LinkNode shortHead = len1 >= len2? head2 : head1;
        while (abs-- != 0){
            lenHead = lenHead.getNext();
        }
        boolean isFirst = true;
        while ((lenHead != loop1 || lenHead != loop2) || isFirst){
            if (lenHead == loop1 || lenHead == loop2){
                // 第一次遇到入环点
                isFirst = false;
            }
            if (lenHead == shortHead){
                res = lenHead;
                break;
            }
            lenHead = lenHead.getNext();
            shortHead = shortHead.getNext();
        }
        //if (loop1 != null && loop2 != null && loop1 == loop2){
        //    res = loop1;
        //}
        return res;
    }

    public static void main(String[] args) {
        LinkNode head1 = CommonUtils.getLinkNodeListByArr(new int[]{1, 2, 3, 4, 5});
        LinkNode head2 = CommonUtils.getLinkNodeListByArr(new int[]{6, 7, 8, 9, 0});
        // 成环接入
        LinkNode commonLoop = CommonUtils.getLinkNodeListByArr(new int[]{11, 12, 13});
        LinkNode node13 = CommonUtils.findFirstNodeByValue(commonLoop, 13);
        node13.setNext(commonLoop);
        LinkNode node12 = CommonUtils.findFirstNodeByValue(commonLoop, 12);

        LinkNode node3 = CommonUtils.findFirstNodeByValue(head1, 3);
        LinkNode node5 = CommonUtils.findFirstNodeByValue(head1, 5);

        LinkNode node9 = CommonUtils.findFirstNodeByValue(head2, 9);
        LinkNode node0 = CommonUtils.findFirstNodeByValue(head2, 0);

        // 情况一
         0-9
        //node0.setNext(node9);
         5-3
        //node5.setNext(node3);

        // 情况二
        // 9->3
        //node9.setNext(node3);

        // 情况三：什么都不做，没有焦点
        // 情况四：
        //node5.setNext(commonLoop);
        //node0.setNext(node3);
        // 情况五：
        //node5.setNext(commonLoop);
        //node0.setNext(commonLoop);
        // 情况六
        node0.setNext(commonLoop);
        node5.setNext(node12);
        System.out.println(myGetCross(head1, head2));
    }
}

c语言版本

正在学习中

c++语言版本

正在学习中

思考感悟

1、怎么想到的？
不看书我只想到了单链表无环的情况，看了书发现单链表还有环，这样的话分析起来就比较多了，不过慢慢想，应该都能想到这些情况，论读书的重要性~
2、关键逻辑
· 判断是否有环的方式需要注意：快慢节点相遇来判断
· 入环点的寻找：快节点和慢节点寻找入环点非常巧妙，跟数学有关
· 入环点不同时注意有一种相交和不相交的情况
· 入环点相同是注意有环外和环内的情况
· 注意遍历时，入环点会先遇到一次，需要第二次遇到入环点才是遍历结束条件哦
3、以后遇到什么样的题用这种思维考虑？
存在环，判断是否有环，入环点在哪的方法在这里可以记一下，复杂度都是O（n）方法比较新颖，还有就是单链表存在环这个在以后考虑情况的时候可以多留一个心眼。

写在最后

方案和代码仅提供学习和思考使用，切勿随意滥用！如有错误和不合理的地方，务必批评指正~
如果需要git源码可咨询2260755767@qq.com或在评论区回复即可.
再次感谢左大神的书对我算法的指点迷津！

最后

以上就是呆萌蛋挞为你收集整理的【算法】【链表模块】两个单链表寻找交点前言问题介绍解决方案代码编写思考感悟写在最后的全部内容，希望文章能够帮你解决【算法】【链表模块】两个单链表寻找交点前言问题介绍解决方案代码编写思考感悟写在最后所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。