一、前提须知
- 图是一种数据结构,一般作为一种模型用来定义对象之间的关系或联系。对象:顶点(
V)表示;对象之间的关系或者关联:通过图的边(E)来表示。一般oj题中可能就是点与点,也有可能是具体生活中的物体 - 图分为有向图和无向图,图的存储使用邻接矩阵(即二维数组)或者邻接表。
- 图的最基本操作就是图的遍历,深度优先搜索算法(dfs)和广度优先搜索算法(bfs)是图遍历操作的2种方法。这2钟方法对于无向图和有向图皆适用。
二、深度优先搜索算法(dfs)
1.基本思想:
简单说就是搜到底,重新搜。从v0为起点进行搜索,如果被访问过,则做一个标记,直到与v0想连通的点都被访问一遍,如果这时,仍然有点没被访问,可以从中选一个顶点,进行再一次的搜索,重复上述过程。
2.代码思想:
定义一个二维数组存放点与点之间的关系,可以直接到达即为1,否则为0;
定义一个一维数组用于记录某个点是否已经访问过。初始化全为0,代表都未访问过。
使用递归方法,得出结果。
3.例子:
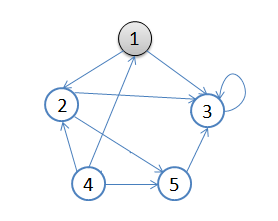
( 网图)
- 以任何一个点为起点,如 顶点 1 。
- 从顶点1开始搜索,为 1->2->3 ,到顶点3后终止。回溯到顶点 2 .
- 2->5 到达顶点5 后终止。回溯 到 顶点2,终止于顶点2,回溯到 顶点 1,终止于顶点 1.
- 从顶点 4 开始访问,并终止于顶点 4 。
实现上述图的递归dfs代码:
#include <iostream>
using namespace std;
const int maxn=100;
int arr[maxn][maxn];
int vis[maxn + 1] = { 0 };
int n;
void dfs(int start)
{
vis[start]=1;
for(int i=1;i<=n;i++)
{
if(!vis[i]&&arr[start-1][i-1]==1)
dfs(i);
}
cout<<start<<" ";
}
void dfs_traverse(int begin)
{
dfs(begin);
for(int i=1;i<=n;i++)//例子中的点是从1开始的,所以是1到n(dfs中同理);
{
if(vis[i]==1)
continue;
dfs(i);
}
}
int main()
{
int i,j,begin;
//读入总的顶点数
cin>>n;
//读入邻接矩阵
for(i=0;i<n;i++)
for(j=0;j<n;j++)
cin>>arr[i][j];
//输入深度搜索的起始顶点
cin>>begin;
dfs_traverse(begin);
return 0;
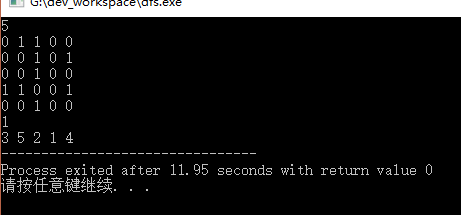
}测试数据:
0 1 1 0 0
0 0 1 0 1
0 0 1 0 0
1 1 0 0 1
0 0 1 0 0
结果:
三、广度优先搜索算法(bfs)
1.基本思想:
选择一个顶点为起始顶点,先搜索与该点连接的所有的邻点,依次搜索所有邻点的邻点。
2.代码思想:
双端队列不为空则循环
将未访问的邻接点压入双端链表后面,然后从前面取出并访问
结合上述2点,使用STL中的queue实现起来可以方便一点
3.例子:
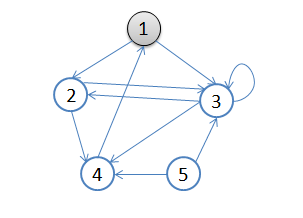
从顶点1开始进行广度优先搜索:
- 初始状态,从顶点1开始,队列={1}
- 访问1的邻接顶点,1出队变黑,2,3入队,队列={2,3,}
- 访问2的邻接结点,2出队,4入队,队列={3,4}
- 访问3的邻接结点,3出队,队列={4}
- 访问4的邻接结点,4出队,队列={ 空}
结点5对于1来说不可达。
实现上述的bfs代码:
#include <iostream>
#include<queue>
using namespace std;
const int maxn=100;
int arr[maxn][maxn];
int vis[maxn + 1] = { 0 };
int n;
void bfs(int start)
{
queue<int>q;
q.push(start);
vis[start]=1;
while(!q.empty())
{
int front=q.front();
cout<<front<<" ";
q.pop();
for(int i=1;i<=n;i++)
{
if(!vis[i]&&arr[front-1][i-1])
{
vis[i]=1;
q.push(i);
}
}
}
}
void bfs_traverse(int begin)
{
bfs(begin);
for(int i=1;i<=n;i++)//例子中的点是从1开始的,所以是1到n(bfs中同理);
{
if(vis[i]==1)
continue;
bfs(i);
}
}
int main()
{
int i,j,begin;
//读入总的顶点数
cin>>n;
//读入邻接矩阵
for(i=0;i<n;i++)
for(j=0;j<n;j++)
cin>>arr[i][j];
//输入深度搜索的起始顶点
cin>>begin;
bfs_traverse(begin);
return 0;
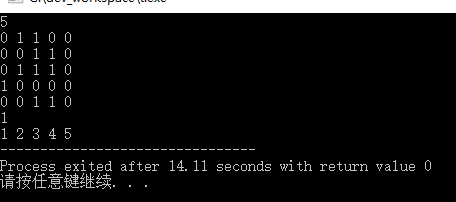
}测试数据:
0 1 1 0 0
0 0 1 1 0
0 1 1 1 0
1 0 0 0 0
0 0 1 1 0
测试结果:
最后
以上就是迷路汽车最近收集整理的关于图的遍历算法-深度优先搜索算法(dfs)和广度优先搜索算法(bfs)的全部内容,更多相关图内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。






![C语言 PTA 合并两个有序数组-[一维数组]题目: 代码:](https://www.shuijiaxian.com/files_image/reation/bcimg1.png)

发表评论 取消回复