2021-11-6 78. 子集（回溯）

注：

题目：
给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2：
输入：nums = [0]
输出：[[],[0]]

提示：
1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

题解：
思路
如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！

其实子集也是一种组合问题，因为它的集合是无序的，子集{1,2} 和 子集{2,1}是一样的。

那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始，而不是从0开始！

有同学问了，什么时候for可以从0开始呢？

求排列问题的时候，就要从0开始，因为集合是有序的，{1, 2} 和{2, 1}是两个集合，排列问题我们后续的文章就会讲到的。

以示例中nums = [1,2,3]为例把求子集抽象为树型结构，如下：

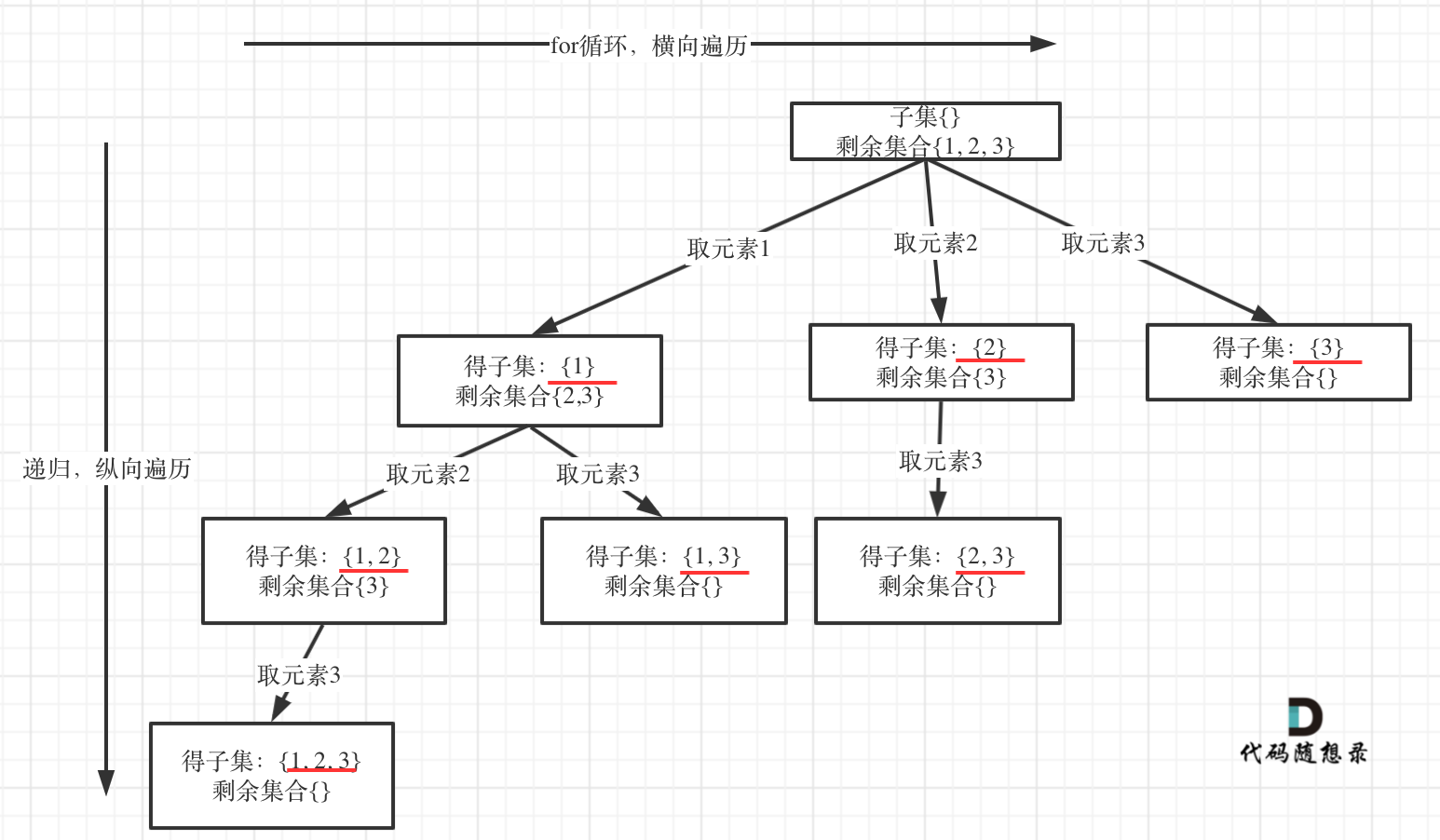
从图中红线部分，可以看出遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合。

复杂度分析
时间复杂度：O(n×2ⁿ)。一共 2ⁿ个状态，每种状态需要 O(n)O 的时间来构造子集。

空间复杂度：O(n)。即构造子集使用的临时数组 t 的空间代价。

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums,int index){
        if(index>nums.size()){
            return ;
        }
        for(int i=index;i<nums.size();i++){
            path.push_back(nums[i]);
            result.push_back(path);
            backtracking(nums,i+1);
            path.pop_back();   
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        result.push_back(path);
        backtracking(nums,0);
        return result;
    }
};

最后

以上就是曾经黑夜为你收集整理的2021-11-6 78. 子集（回溯）的全部内容，希望文章能够帮你解决2021-11-6 78. 子集（回溯）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。