目录
- 循环神经网络RNN
- 1.公式推导
- 2.代码实现
循环神经网络RNN
1.公式推导
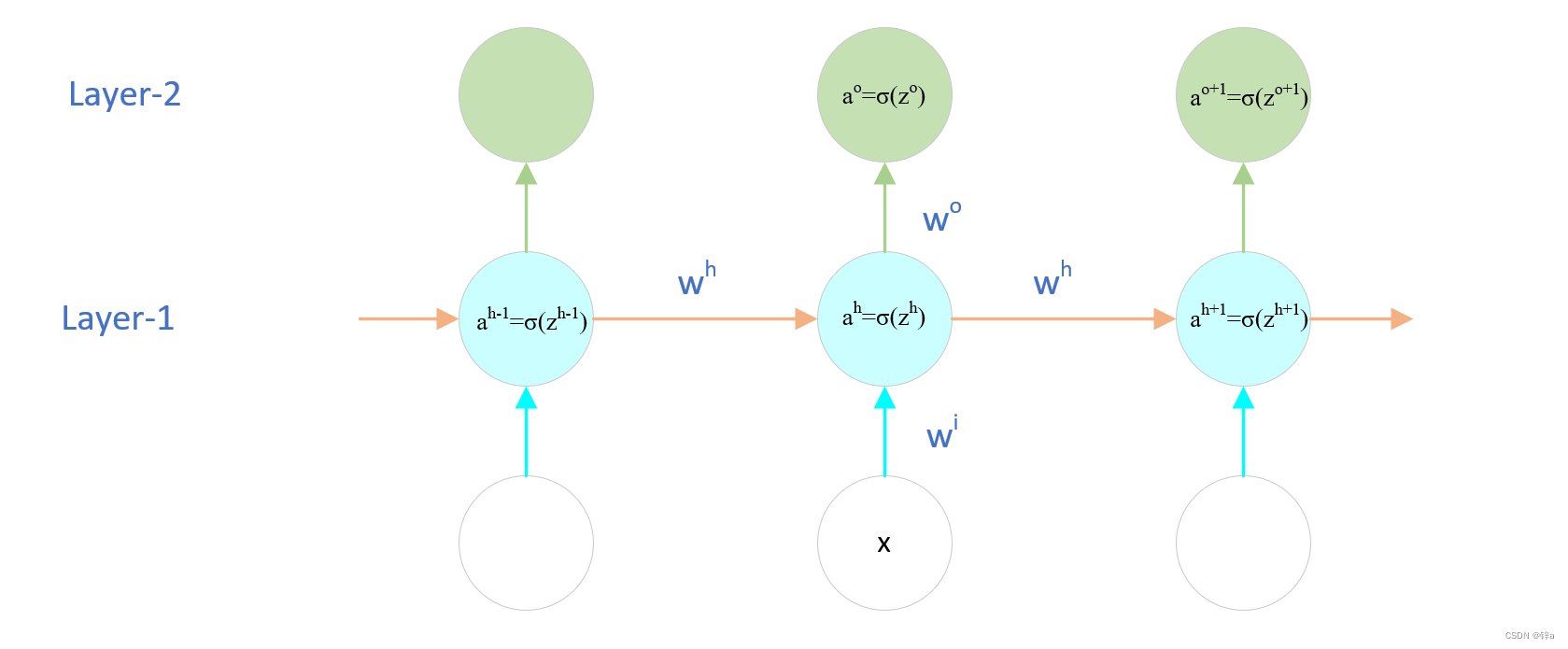
对于该循环神经网络,以中间的RNN单元为例,推导前向传播:
对于Layer-1:
z h = w i x + w h a h − 1 z^h = w^ix+w^ha^{h-1} zh=wix+whah−1
a h = σ ( z h ) a^h = sigma(z^h) ah=σ(zh)
这里 σ sigma σ是 s i g m o i d ( ⋅ ) sigmoid(·) sigmoid(⋅)激活函数
对于Layer-2:
z o = w o a h z^o = w^oa^h zo=woah
p r e d = a o = σ ( z o ) pred = a^o=sigma(z^o) pred=ao=σ(zo)
这里pred即RNN的输出
为了更新三个权值参数 w i , w h , w o w^i,w^h,w^o wi,wh,wo的值,需要求梯度进行反向传播:
首先确立损失函数为平方误差,加上
1
2
frac{1}{2}
21是为了便于求导。
l
o
s
s
=
1
2
(
y
−
p
r
e
d
)
2
loss = frac12(y-pred)^2
loss=21(y−pred)2
对
w
o
w^o
wo进行求导:
∂
l
o
s
s
∂
w
o
=
∂
l
o
s
s
∂
p
r
e
d
×
∂
p
r
e
d
∂
z
o
×
∂
z
o
∂
w
o
=
−
(
y
−
p
r
e
d
)
×
(
a
o
)
(
1
−
a
o
)
×
(
a
h
)
frac{partial loss}{partial w^o} = frac{partial loss}{partial pred}times frac{partial pred}{partial z^o} times frac{partial z^o}{partial w^o} = -(y-pred)times(a^o)(1-a^o)times(a^h)
∂wo∂loss=∂pred∂loss×∂zo∂pred×∂wo∂zo=−(y−pred)×(ao)(1−ao)×(ah)
注意这里
s
i
g
m
o
i
d
(
)
sigmoid()
sigmoid()函数
f
(
x
)
f(x)
f(x)的求导为
f
(
x
)
(
1
−
f
(
x
)
)
f(x)(1-f(x))
f(x)(1−f(x))
再对
w
h
w^h
wh进行求导:
∂
l
o
s
s
∂
w
h
=
∂
l
o
s
s
n
o
w
∂
w
h
+
∂
l
o
s
s
n
e
x
t
∂
w
h
frac{partial loss}{partial w^h} = frac{partial loss^{now}}{partial w^h}+ frac{partial loss^{next}}{partial w^h}
∂wh∂loss=∂wh∂lossnow+∂wh∂lossnext
由于
w
h
w^h
wh不仅影响到当前RNN单元的损失,还影响到下一个RNN单元的损失,所以梯度要分两部分算
∂
l
o
s
s
n
o
w
∂
w
h
=
∂
l
o
s
s
n
o
w
∂
p
r
e
d
×
∂
p
r
e
d
∂
z
o
×
∂
z
o
∂
a
h
×
∂
a
h
∂
z
h
×
∂
z
h
∂
w
h
=
−
(
y
−
p
r
e
d
)
×
(
a
o
)
(
1
−
a
o
)
×
w
o
a
h
(
1
−
a
h
)
×
a
h
−
1
frac{partial loss^{now}}{partial w^h} = frac{partial loss^{now}}{partial pred}times frac{partial pred}{partial z^o} times frac{partial z^o}{partial a^h}timesfrac{partial a^h}{partial z^h}times frac{partial z^h}{partial w^h} \= -(y-pred)times(a^o)(1-a^o)times w^oa^h(1-a^h)times a^{h-1}
∂wh∂lossnow=∂pred∂lossnow×∂zo∂pred×∂ah∂zo×∂zh∂ah×∂wh∂zh=−(y−pred)×(ao)(1−ao)×woah(1−ah)×ah−1
∂ l o s s n e x t ∂ w h = ∂ l o s s n e x t ∂ p r e d n e x t × ∂ p r e d n e x t ∂ z o + 1 × ∂ z o + 1 ∂ a h + 1 × ∂ a h + 1 ∂ z h + 1 × ∂ z h + 1 ∂ a h × ∂ a h ∂ z h × ∂ z h ∂ w h = w h δ ( n e x t ) × a h ( 1 − a h ) × a h − 1 frac{partial loss^{next}}{partial w^h} = frac{partial loss^{next}}{partial pred^{next}}times frac{partial pred^{next}}{partial z^{o+1}} times frac{partial z^{o+1}}{partial a^{h+1}}times frac{partial a^{h+1}}{partial z^{h+1}}timesfrac{partial z^{h+1}}{partial a^h} timesfrac{partial a^h}{partial z^h}times frac{partial z^h}{partial w^h}\=w^hdelta(next)times a^h(1-a^h)times a^{h-1} ∂wh∂lossnext=∂prednext∂lossnext×∂zo+1∂prednext×∂ah+1∂zo+1×∂zh+1∂ah+1×∂ah∂zh+1×∂zh∂ah×∂wh∂zh=whδ(next)×ah(1−ah)×ah−1
为了简写公式,这里的 δ ( n e x t ) delta(next) δ(next)指的是后面一个RNN单元对自己 z h + 1 z^{h+1} zh+1的求导过程,下面的 δ ( n o w ) delta(now) δ(now)同理
两者相加即可得
w
h
w^h
wh的梯度,对矩阵求导不自信的话,在推的时候可以拟定一下维度确定要不要转置矩阵(我的公式可能存在笔误,欢迎指出):
∂
l
o
s
s
∂
w
h
=
[
(
w
h
)
T
δ
(
n
e
x
t
)
+
(
w
o
)
T
δ
(
n
o
w
)
]
×
a
h
(
1
−
a
h
)
×
a
h
−
1
frac{partial loss}{partial w^h} = left[{(w^h)}^Tdelta(next) + (w^o)^Tdelta(now)right]times a^h(1-a^h)times a^{h-1}
∂wh∂loss=[(wh)Tδ(next)+(wo)Tδ(now)]×ah(1−ah)×ah−1
最后求
w
i
w^i
wi,连续偏导部分与
∂
l
o
s
s
n
o
w
∂
w
h
largefrac{partial loss^{now}}{partial w^h}
∂wh∂lossnow基本一致,最后一项改为
x
x
x:
∂
l
o
s
s
∂
w
i
=
−
(
y
−
p
r
e
d
)
×
(
a
o
)
(
1
−
a
o
)
×
w
o
a
h
(
1
−
a
h
)
×
x
T
frac{partial loss}{partial w^i} = -(y-pred)times(a^o)(1-a^o)times w^oa^h(1-a^h)times x^T
∂wi∂loss=−(y−pred)×(ao)(1−ao)×woah(1−ah)×xT
2.代码实现
我们的基本认为是给定两个八位二进制的数,让RNN预测两个相加的结果,输出八位二进制数,在两数相加中涉及到一个进位的问题,所以RNN学习的就是怎么在循环中进位。如下图所示,注意在该情况下,前向传播是从低位数开始的,所以是从八位二进制数的右边往左边走,而反向传播则是从左往右走。
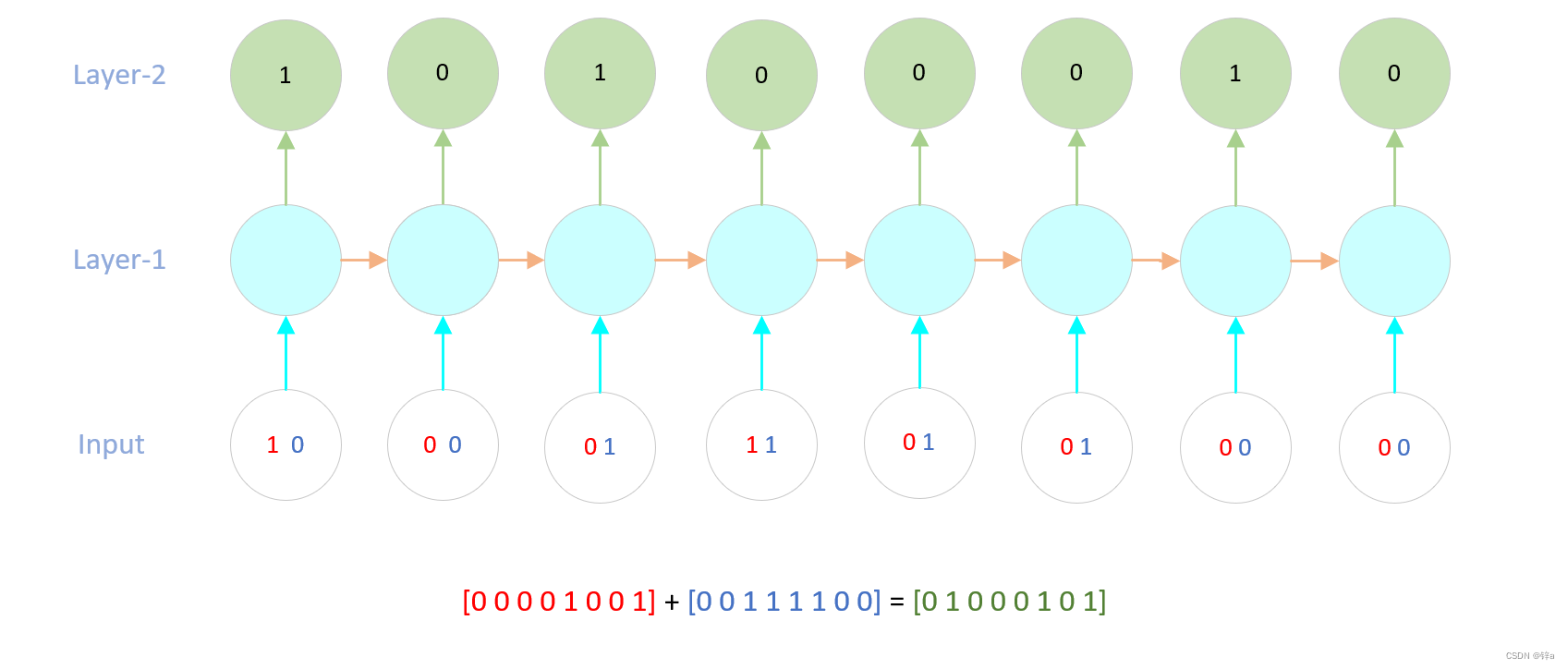
根据之前的公式推理,要实现这个简单的RNN,我们需要做这些事:
- 存储上一个RNN单元的 a h a^h ah值,即公式中的 a h − 1 a^{h-1} ah−1
- 存储未来的RNN单元求导至 z h z^h zh的值,即公式中的 δ ( n e x t ) delta(next) δ(next)
- 创建一些列表,存储每个单元的值,便于使用
我们发现,在公式中有很多重复的乘法计算,我们将其中的重复计算存储起来,就可以便于理解和代码实现,定义如下:
- layer_2_deltas :表示输出层的误差,存储的是 ( y − p r e d ) × ( a o ) ( 1 − a o ) (y-pred)times(a^o)(1-a^o) (y−pred)×(ao)(1−ao)这一段
- layer_2_values:表示的输出层的值,即 p r e d pred pred
- layer_1_values:表示的是第一层的值,即 a h a^h ah
- future_layer_1_delta:表示的是下一个RNN单元求导至 z h + 1 z^{h+1} zh+1的值,即 δ ( n e x t ) delta(next) δ(next)
- layer_1_delta:表示的是当前RNN单元求导至 z h z^h zh的值,即 δ ( n e x t ) delta(next) δ(next),我们将这个值存储起来作为上一个RNN反向传播时的future_layer_1_delta
你将在代码中看到这些变量,如果不明白这些变量的意思,随时回来看看
代码如下,参考自博客csdn博客,在他的基础上做了修改,并添加了非常详细的注释,相信大家都能看懂。
import copy
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0) #随机种子,固定的话每个人得到的结果都一致
# sigmoid函数
def sigmoid(x):
output = 1 / (1 + np.exp(-x))
return output
# sigmoid导数
def sigmoid_output_to_derivative(output):
return output * (1 - output)
# 训练数据生成
int2binary = {}
binary_dim = 8
largest_number = pow(2, binary_dim) #2的8次方,共256个数
binary = np.unpackbits(
np.array([range(largest_number)], dtype=np.uint8).T, axis=1)
# unpackbits函数可以把整数转化成2进制数
for i in range(largest_number):
int2binary[i] = binary[i] #形成一个映射,将0-255的数映射到对应的二进制
# 初始化一些变量
alpha = 0.1 #学习率
input_dim = 2 #输入的大小,因为是2个数相加,所以是2
hidden_dim = 16 #隐含层的大小,代表记忆的维度,这里可以设置任意值
output_dim = 1 #输出层的大小,输出一个结果,所以是1
EPOCHS = 10000 #迭代次数,即共训练多少次
Eval = 100 #每迭代多少次验证一次
# 随机初始化权重
w_i = 2 * np.random.random((hidden_dim, input_dim)) - 1 #输入的权值矩阵,维度为(16, 2)
w_o = 2 * np.random.random((output_dim, hidden_dim)) - 1 #输出的权值矩阵,维度为(1, 16)
w_h = 2 * np.random.random((hidden_dim, hidden_dim)) - 1 #循环rnn的关键,隐藏层与隐藏层之间的权值矩阵,维度为(16, 16)
w_i_update = np.zeros_like(w_i) #w_i的梯度,维度(16, 2)
w_o_update = np.zeros_like(w_o) #w_o的梯度,维度(1, 16)
w_h_update = np.zeros_like(w_h) #w_h的梯度,维度(16, 16)
# 开始训练
error_num_list = []
for j in range(EPOCHS):
#每次随机生成两个128以内的数进行相加(防止溢出),并将相加的结果作为标签
# 二进制相加
a_int = np.random.randint(largest_number / 2) # 随机生成相加的数
a = int2binary[a_int] # 映射成二进制值
b_int = np.random.randint(largest_number / 2) # 随机生成相加的数
b = int2binary[b_int] # 映射成二进制值
# 真实的答案
label_int = a_int + b_int #结果
label = int2binary[label_int] #映射成二进制值
# 待存放预测值,这里我们要输出8位二进制,所以维度是8,即rnn输出8次
prediction = np.zeros_like(label)
overallError = 0 # rnn输出的8个值错了几个
layer_2_deltas = list() #输出层的误差
layer_2_values = list() #第二层的值(输出的结果)
layer_1_values = list() #第一层的值(隐含状态)
layer_1_values.append(copy.deepcopy(np.zeros((hidden_dim, 1)))) #第一个隐含状态需要0作为它的上一个隐含状态
#前向传播
for i in range(binary_dim):
X = np.array([[a[binary_dim - i - 1], b[binary_dim - i - 1]]]).T #将两个输入并起来变为矩阵,维度(2,1)
y = np.array([[label[binary_dim - i - 1]]]).T #将y也变为矩阵,维度(1,1)
layer_1 = sigmoid(np.dot(w_h, layer_1_values[-1]) + np.dot(w_i, X)) #先算第一层,算到ah,维度(1,1)
layer_1_values.append(copy.deepcopy(layer_1)) #将第一层的值存储起来,方便反向传播用
layer_2 = sigmoid(np.dot(w_o, layer_1)) #算输出层的值,维度(1,1)
#loss = 1/2(y-pred)^2 没有必要写了,直接写梯度就行
error = -(y-layer_2) #损失对pred求导,记得这里pred = layer_2
layer_delta2 = error * sigmoid_output_to_derivative(layer_2) # 这里是输出层求导至zo的那一段,(1,1)
layer_2_deltas.append(copy.deepcopy(layer_delta2)) #存储起来反向传播用
prediction[binary_dim - i - 1] = np.round(layer_2[0][0]) #预测值,[0][0]是为了把1*1矩阵变成数
future_layer_1_delta = np.zeros((hidden_dim, 1)) #这个是未来一个RNN单元求导至zh的δ(next),存起来求wh用的
#反向传播
for i in range(binary_dim): #对于8位数,之前是从右往左前向传播,所以现在是从左往右反向传播
X = np.array([[a[i], b[i]]]).T
prev_layer_1 = layer_1_values[-i-2] #前一个RNN单元的值,因为包含初始化的0值层(第一个RNN单元的pre是0),所以-2
layer_1 = layer_1_values[-i-1] #当前的隐藏层值
layer_delta2 = layer_2_deltas[-i-1] #将之前存着的输出层的误差求导取出来
layer_delta1 = np.multiply(np.add(np.dot(w_h.T, future_layer_1_delta),np.dot(w_o.T, layer_delta2)), sigmoid_output_to_derivative(layer_1)) #根据当前的误差以及未来一层的误差求当前的wh
w_i_update += np.dot(layer_delta1, X.T) #根据公式还要再乘上一项才是梯度
w_h_update += np.dot(layer_delta1, prev_layer_1.T)
w_o_update += np.dot(layer_delta2, layer_1.T)
future_layer_1_delta = layer_delta1
w_i -= alpha * w_i_update
w_h -= alpha * w_h_update
w_o -= alpha * w_o_update
w_i_update *= 0
w_o_update *= 0
w_h_update *= 0
# 验证结果
if (j % Eval == 0): #每100次验证一次
overallError = sum([1 if prediction[i] != label[i] else 0 for i in range(binary_dim)])#错了几个
error_num_list.append(overallError)
print("Error:" + str(overallError))
print("Pred:" + str(prediction))
print("True:" + str(label))
out = 0
for index, x in enumerate(reversed(prediction)): #二进制还原为10进制
out += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out))
print("------------")
plt.plot(np.arange(len(error_num_list))*Eval, error_num_list)
plt.ylabel('Error numbers')
plt.xlabel('Epochs')
plt.show()
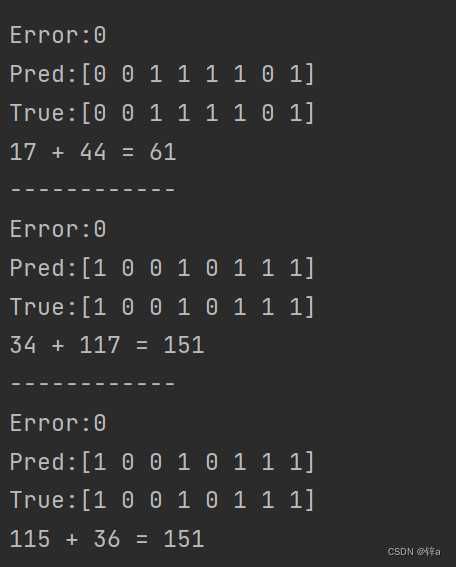
得到的部分结果:
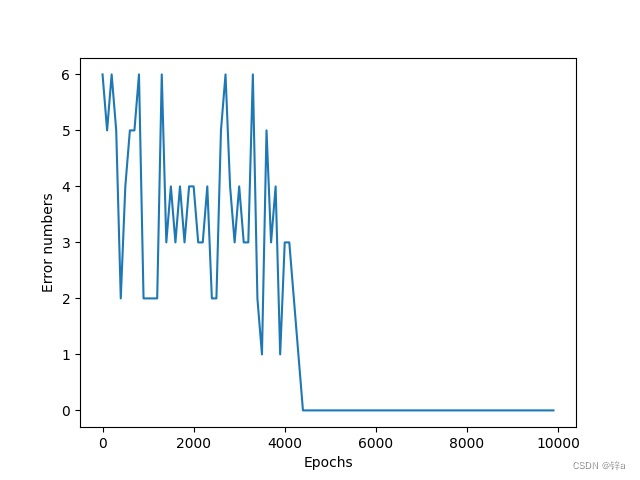
预测error的下降趋势,这里表示的是8位二进制数中错误的个数
最后
以上就是潇洒彩虹最近收集整理的关于Python手撸机器学习系列(十六):循环神经网络RNN的实现循环神经网络RNN的全部内容,更多相关Python手撸机器学习系列(十六):循环神经网络RNN内容请搜索靠谱客的其他文章。








发表评论 取消回复