纯手工
- 一.BP神经网络
- 1.一图知其意
- 2.多言以述之
- 二.BP算法
- 1.参数初始化
- 2.前向传播
- 3.反向传播
- 三.具体细节
- 四.手工计算
- 5.代码实现
一.BP神经网络
1.一图知其意
????

2.多言以述之
????????????
BP算法包括信号的前向传播和误差的反向传播两个过程。即计算误差输出时按从输入到输出的方向进行,而调整权值和阈值则从输出到输入的方向进行。
正向传播时,输入信号通过隐含层作用于输出节点,经过非线性变换,产生输出信号,若实际输出与期望输出不相符,则转入误差的反向传播过程。
误差反传是将输出误差通过隐含层向输入层逐层反传,并将误差分摊给各层所有单元,以从各层获得的误差信号作为调整各单元权值的依据。通过调整输入节点与隐层节点的联接强度和隐层节点与输出节点的联接强度以及阈值,使误差沿梯度方向下降,经过反复学习训练,确定与最小误差相对应的网络参数(权值和阈值),训练即告停止。此时经过训练的神经网络即能对类似样本的输入信息,自行处理输出误差最小的经过非线形转换的信息。
二.BP算法
1.参数初始化
????
首先要给定输入、输出、各层之间的权值及偏置。
2.前向传播
????????
1.输入层的每个节点与隐藏层的每个节点都要计算,计算的方法是加权求和+激活。
2.利用隐藏层计算出每个值,再用相同的方法,和输出层的每个结点进行计算。
3.隐藏层用都是用Sigmoid作激活函数。
4.最终的输出值和样本值作比较,计算出误差。
5.开始反向传播。
3.反向传播
????????????
1.利用前向传播最后输出的结果来计算误差的偏导数(前向传播后求偏导)。
2.再用这个偏导数和前面的隐藏层进行加权求和。
3.如此一层一层的向后传下去(隐藏层间偏导加权求和),直到输入层(不计算输入层)。
4.最后利用每个节点求出的偏导数来更新权重。
三.具体细节
????
为了叙述方便,后面用残差(error term)这个词来表示误差的偏导数。学习率是一个预先设置好的参数,用于控制每次更新的幅度。
对于残差的计算公式:
输出层→隐藏层:残差 = -(输出值-样本值) * 激活函数的导数
隐藏层→隐藏层:残差 = (右层每个节点的残差加权求和) * 激活函数的导数
权重更新公式:
输入层→隐藏层:权重增加 = 输入值 * 右层对应节点的残差 * 学习率
隐藏层→输出层:权重增加 = 当前节点的激活函数 * 右层对应节点的残差 * 学习率
此后,对全部数据都反复进行这样的计算,直到输出的误差达到一个很小的值为止。
注意:本文我们采用的激活函数是Sigmoid,而Sigmoid函数的导数就为Sigmoid*(1-Sigmoid)。想了解更多,我这里放了一个链接 常用的激活函数,大家可以自行提取。
四.手工计算
????
首先我们给出一个表格,
x
x
x分别代表2个输入值,
y
y
y代表给定的输出值。
| x 1 x_1 x1 | x 2 x_2 x2 | y y y |
|---|---|---|
| 0.8 | -0.7 | 0.5 |
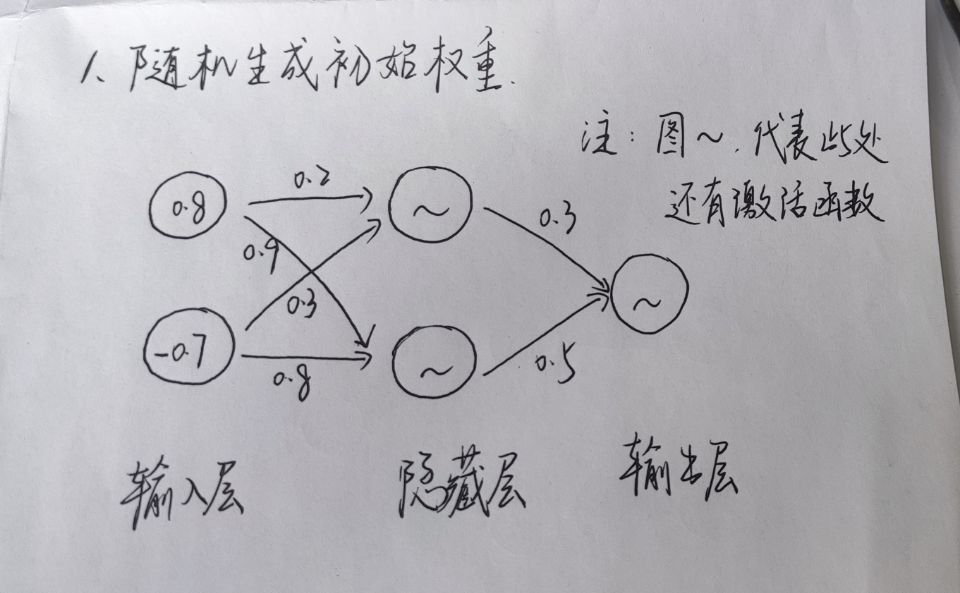
这里的初始权重是用Python库中的random随机生成的。
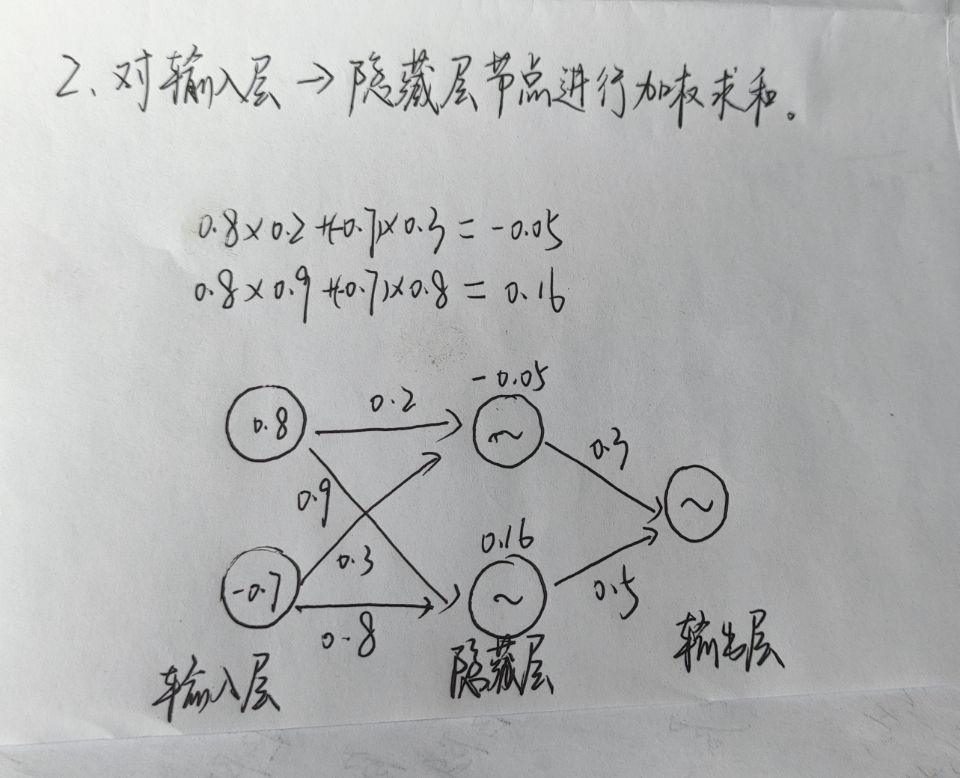
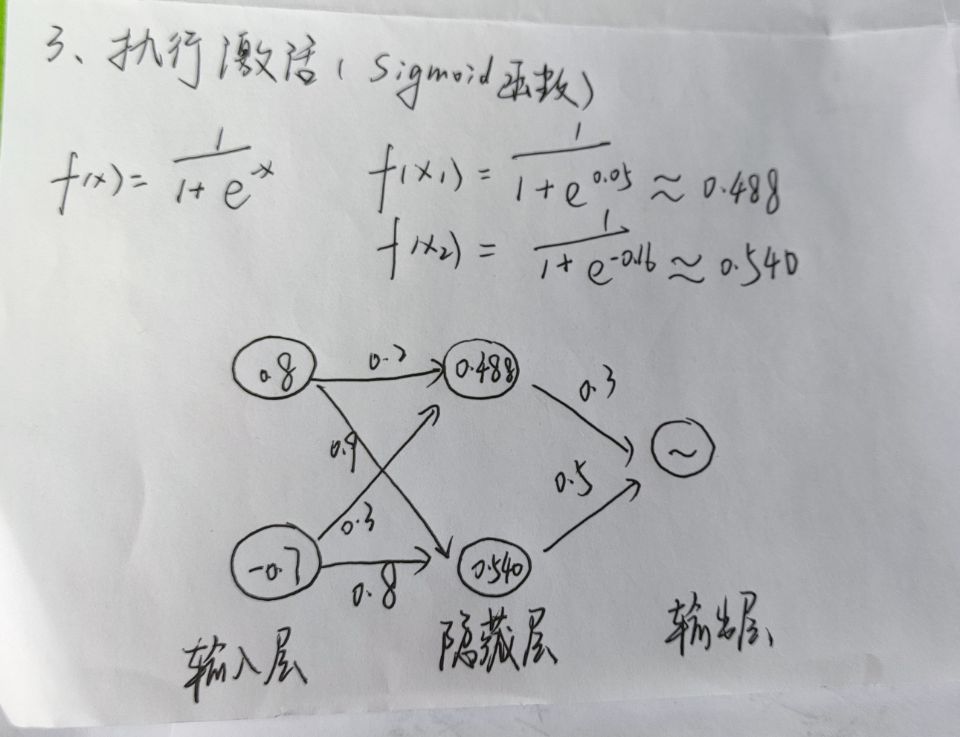
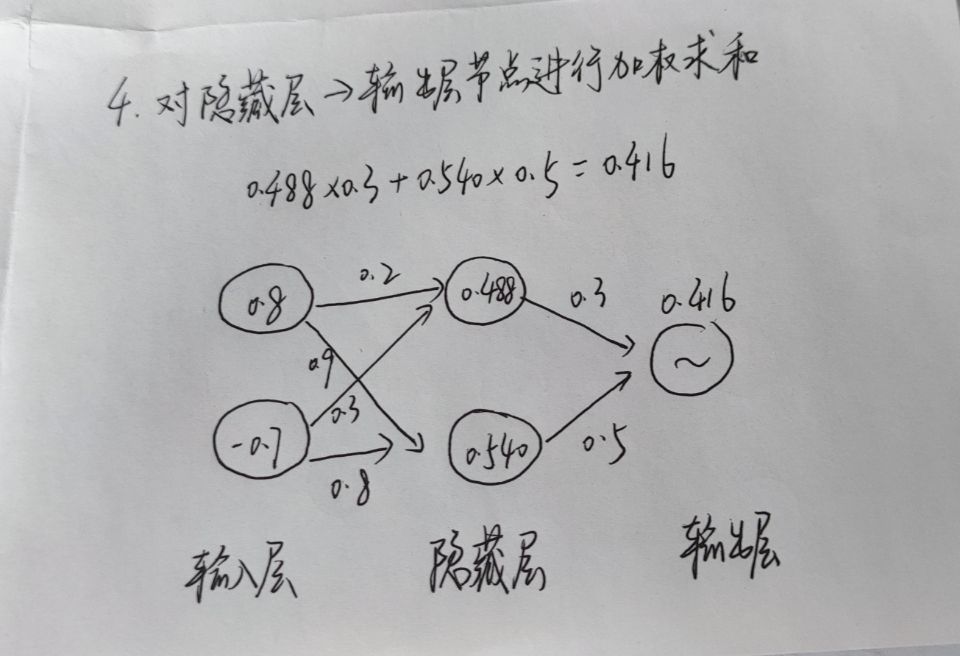
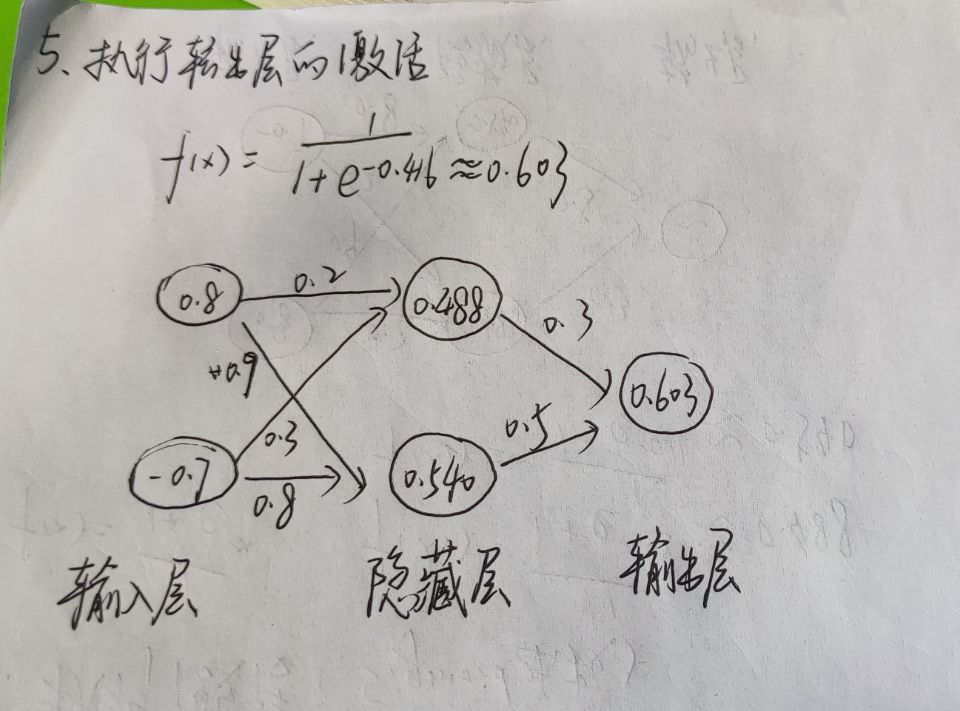
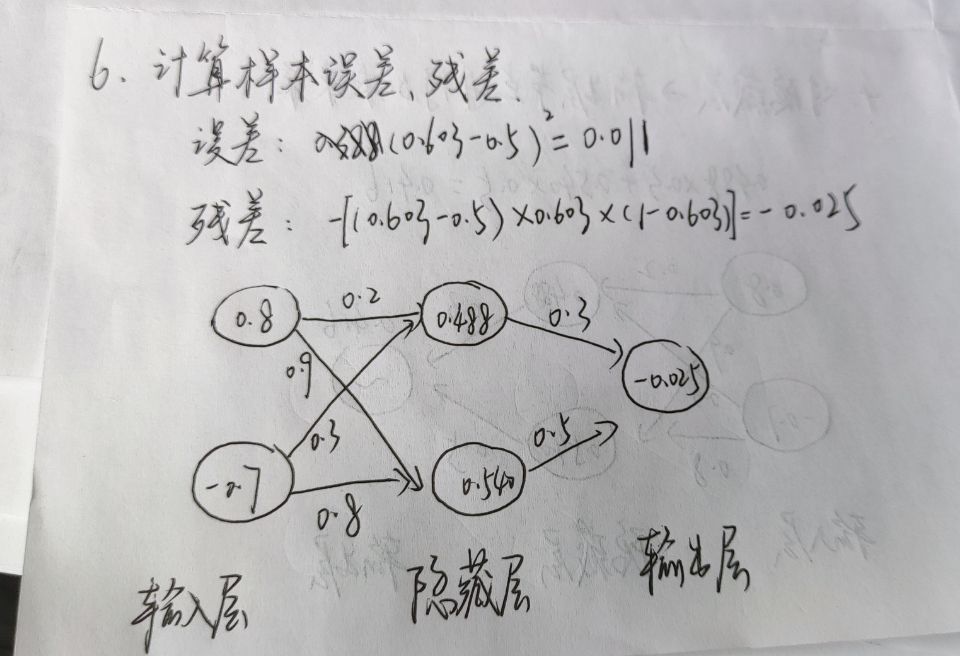
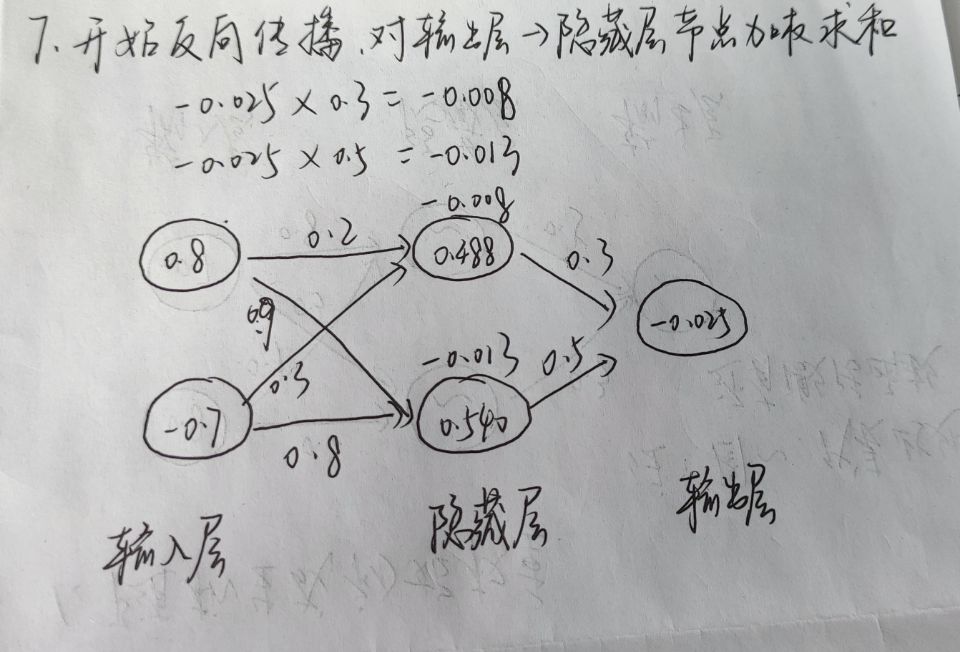
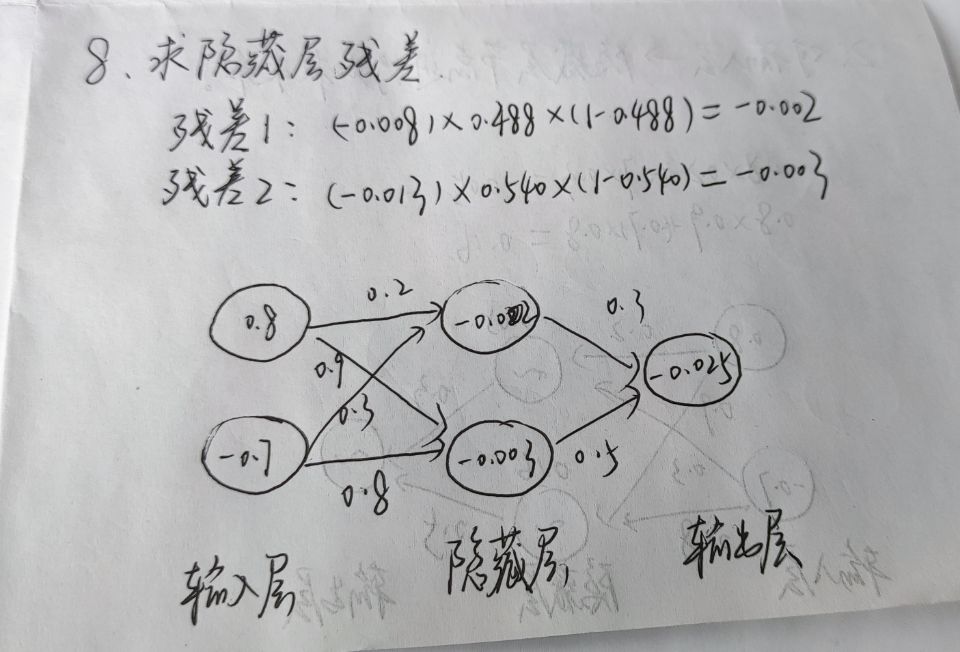

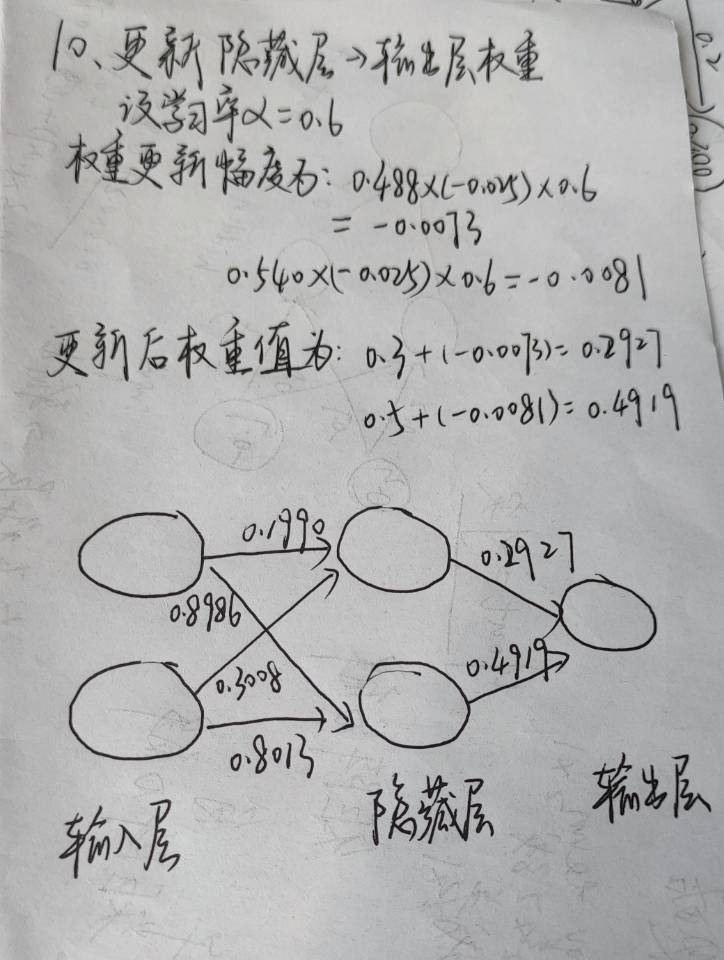
至此,我们就完成了一次的学习,后续就是一次次往这个神经网络放进输入值和输出值,不断更新权重。经过足够多的次数后,我们就能得到想要的结果。
5.代码实现
????
import numpy as np
# 当deriv为默认值False时,进行sigmoid函数的运算;
# 当deriv为True时,对函数求导运算。(其中,求导运算时输入的x值应为函数值而非自变量)
# 定义sigmoid函数
def sigmoid(x, deriv=False):
if (deriv == True):
return x * (1 - x)
else:
return 1 / (1 + np.exp(-x))
# input dataset
X = np.array([[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]])
# output dataset
y = np.array([[0, 1, 1, 0]]).T
# 初始化权重
weight_1 = 2 * np.random.random((3, 4)) - 1
weight_2 = 2 * np.random.random((4, 2)) - 1
weight_3 = 2 * np.random.random((2, 1)) - 1
# 初始化偏置
b1 = 2 * np.random.random((1, 4)) - 1
b2 = 2 * np.random.random((1, 2)) - 1
b3 = 2 * np.random.random((1, 1)) - 1
bias_1 = np.array([b1[0], b1[0], b1[0], b1[0]])
bias_2 = np.array([b2[0], b2[0], b2[0], b2[0]])
bias_3 = np.array([b3[0], b3[0], b3[0], b3[0]])
# 开始训练
for i in range(60000):
I_0 = X
O_0 = I_0
I_1 = np.dot(O_0, weight_1) + bias_1
O_1 = sigmoid(I_1)
I_2 = np.dot(O_1, weight_2) + bias_2
O_2 = sigmoid(I_2)
I_3 = np.dot(O_2, weight_3) + bias_3
O_3 = sigmoid(I_3)
f3_error = y - O_3
if (i % 10000) == 0:
print("Error:" + str(np.mean(f3_error)))
f3_delta = f3_error * sigmoid(O_3, deriv=True)
f2_error = f3_delta.dot(weight_3.T)
f2_delta = f2_error * sigmoid(O_2, deriv=True)
f1_error = f2_delta.dot(weight_2.T)
f1_delta = f1_error * sigmoid(O_1, deriv=True)
weight_3 += O_2.T.dot(f3_delta) # 调整权重
weight_2 += O_1.T.dot(f2_delta)
weight_1 += O_0.T.dot(f1_delta)
bias_3 += f3_delta # 调整偏置
bias_2 += f2_delta
bias_1 += f1_delta
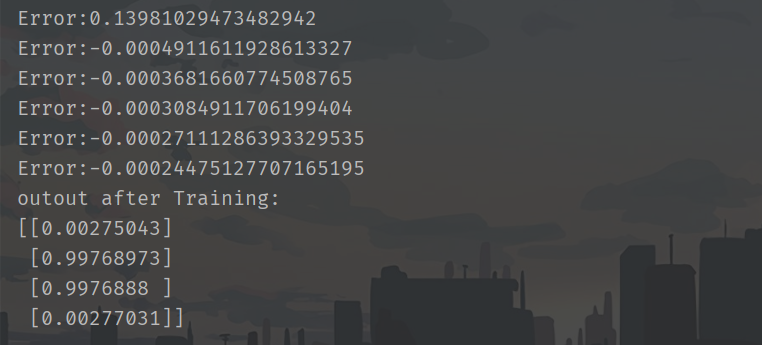
print("outout after Training:")
print(O_3)
参考文章1
参考文章2
最后
以上就是彩色奇异果最近收集整理的关于BP神经网络一.BP神经网络二.BP算法三.具体细节四.手工计算5.代码实现的全部内容,更多相关BP神经网络一内容请搜索靠谱客的其他文章。








发表评论 取消回复