深度剖析数据在内存中的存储1. 数据类型详细介绍2. 整形在内存中的存储：原码、反码、补码3. 大小端字节序介绍及判断4. 浮点型在内存中的存储解析

53 阅读 0 评论 35 点赞

我是靠谱客的博主辛勤嚓茶，最近开发中收集的这篇文章主要介绍深度剖析数据在内存中的存储1. 数据类型详细介绍2. 整形在内存中的存储：原码、反码、补码3. 大小端字节序介绍及判断4. 浮点型在内存中的存储解析，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

深度剖析数据在内存中的存储

1. 数据类型详细介绍
2. 整形在内存中的存储：原码、反码、补码
3. 大小端字节序介绍及判断
4. 浮点型在内存中的存储解析

> 博主水平有限，如果发现错误，一定要及时告知作者哦 o(￣︶￣)o！感谢感谢！
> 博主的码云 gitee，平常博主写的程序代码都在里面。

1. 数据类型详细介绍

????基本的内置类型：

char //字符数据类型
short //短整型
int //整形
long //长整型
long long   //更长的整形
float //单精度浮点数
double //双精度浮点数

????类型的意义：

使用这个类型开辟内存空间的大小（大小决定了使用范围）。
如何看待内存空间的视角

????类型的基本归类：

整型家族：

2.浮点数家族：

在这里插入图片描述
3.构造类型：

4.指针类型：

5.空类型：

void 表示空类型（无类型）通常应用于函数的返回类型、函数的参数、指针类型。

2. 整形在内存中的存储：原码、反码、补码

1. 原码
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:

[+1]原 = 0000 0001
[-1]原 = 1000 0001

第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是: [1111 1111 , 0111 1111] （即 [-127 , 127]）

原码是人脑最容易理解和计算的表示方式.

2. 反码
反码的表示方法是:

正数的反码是其本身

负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.

[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反

可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.

3. 补码
补码的表示方法是:

正数的补码就是其本身

负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补

对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.

????正数的原、反、补码都相同。

????对于整形来说：数据存放内存中其实存放的是补码

为什么呢？

????原因在于：

使用补码，可以将符号位和数值域统一处理；
同时，加法和减法也可以统一处理（CPU只有加法器）此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

3. 大小端字节序介绍及判断

????什么大端小端：
大端（存储）模式，是指数据的低位保存在内存的高地址中，而数据的高位，保存在内存的低地
址中；
小端（存储）模式，是指数据的低位保存在内存的低地址中，而数据的高位,，保存在内存的高地
址中。

????为什么有大端和小端：
这是因为在计算机系统中，我们是以字节为单位的，每个地址单
元都对应着一个字节，一个字节为8 bit。但是在C语言中除了8 bit的char之外，还有16 bit的short型，32 bit的long型（要看具体的编译器），另外，对于位数大于8位的处理器，例如16位或者32位的处理器，由于寄存器宽度大于一个字节，那么必然存在着一个如何将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式。
在这里插入图片描述

代码如下：

int main()
{
	int a = 1;
	char b = a;
	if (b == 1)
	{
		printf("小端");
	}
	if (b==0)
		printf("大端");
	return 0;
}

????如图为在VS2019上面测试的结果：
在这里插入图片描述
????一般在pc端上为小端字节序存储

4. 浮点型在内存中的存储解析

????浮点数存储规则：

详细解读：
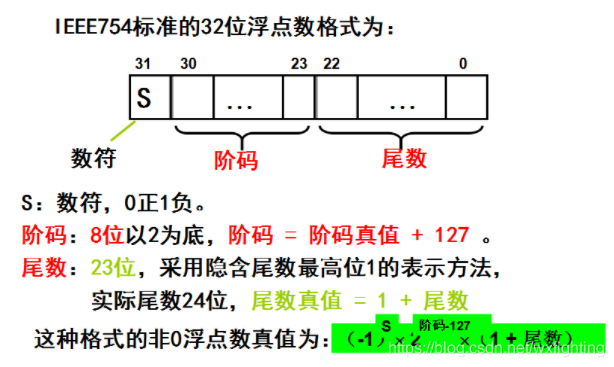
在这里插入图片描述

根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数V可以表示成下面的形式：

(-1)^S * M * 2^E

其中：

(-1)^s表示符号位，当s=0，V为正数；当s=1，V为负数。
M表示有效数字，大于等于1，小于2。
2^E表示指数位。

在这里插入图片描述

对于64位的浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。
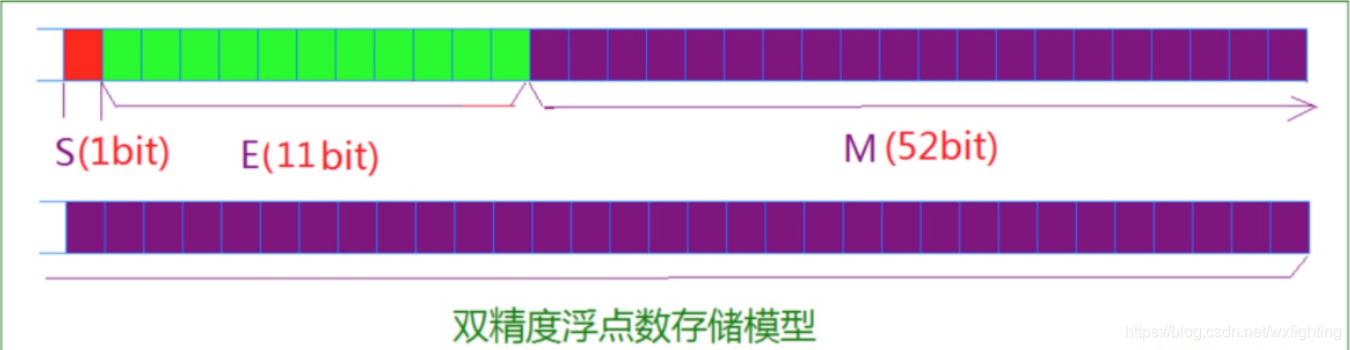
在这里插入图片描述

????IEEE 754对有效数字M和指数E，还有一些特别规定：
1≤M<2 ，也就是说，M可以写成 1.xxxxxx 的形式，其中xxxxxx表示小数部分。
IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的
xxxxxx部分。比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目
的，是节省1位有效数字。以32位浮点数为例，留给M只有23位，将第一位的1舍去以后，等于可以保
存24位有效数字。

至于指数E：
????首先，E为一个无符号整数（unsigned int）

这意味着，如果E为8位，它的取值范围为0255；如果E为11位，它的取值范围为02047。但是，我们知道，科
学计数法中的E是可以出现负数的，所以IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，
对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。比如，2^10的E是10，所以保存
成32位浮点数时，必须保存成10+127=137，即10001001。

????然后，指数E从内存中取出还可以再分成三种情况：

E不全为0或不全为1
这时，浮点数就采用下面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将
有效数字M前加上第一位的1。
比如：0.5的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位，则为
1.0*2^(-1)，其阶码为-1+127=126，表示为01111110，而尾数1.0去掉整数部分为0，补齐0到23
位00000000000000000000000，则其二进制表示形式为: 0 01111110 00000000000000000000000
E全为0
这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，
有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于
0的很小的数字。
E全为1
这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；