机器学习算法练习之（二）：Python和Tensorflow分别实现简单的神经网络

46 阅读 0 评论 31 点赞

我是靠谱客的博主帅气小伙，最近开发中收集的这篇文章主要介绍机器学习算法练习之（二）：Python和Tensorflow分别实现简单的神经网络，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Tensorflow 实现一个三层的神经网络

import numpy as np
import tensorflow as tf
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

#生成数据
np.random.seed(12)
num_observations = 5000
#高斯分布数据
x1 = np.random.multivariate_normal([0, 0], [[2, .75],[.75, 2]], num_observations)
x2 = np.random.multivariate_normal([1, 4], [[1, .75],[.75, 1]], num_observations)
x3 = np.random.multivariate_normal([2, 8], [[0, .75],[.75, 0]], num_observations)

simulated_separableish_features = np.vstack((x1, x2, x3)).astype(np.float32)
simulated_labels = np.hstack((np.zeros(num_observations),
                np.ones(num_observations), np.ones(num_observations) + 1))

plt.figure(figsize=(12,8))
plt.scatter(simulated_separableish_features[:, 0], simulated_separableish_features[:, 1],
            c = simulated_labels, alpha = .4)

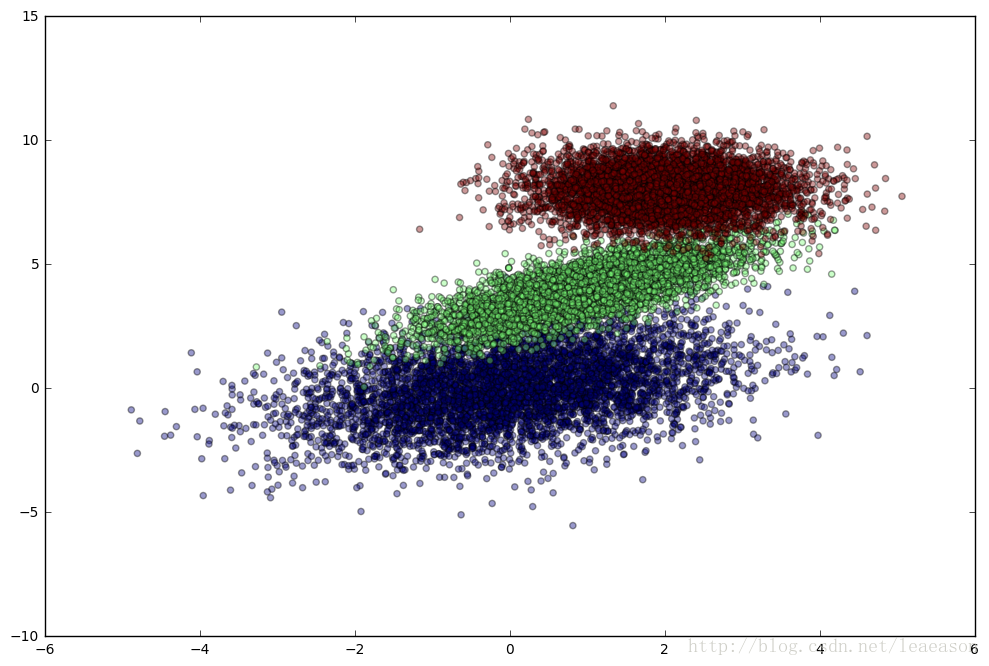
这里写图片描述

准备数据

Tensorflow希望每个特征标签都是一个单独编码的向量，所以我将重新格式化一个模拟标签。
创建一个训练和测试集，以便评估该模型对于数据的泛化程度。

labels_onehot = np.zeros((simulated_labels.shape[0], 3)).astype(int)
labels_onehot[np.arange(len(simulated_labels)), simulated_labels.astype(int)] = 1

train_dataset, test_dataset, 
train_labels, test_labels = train_test_split(
    simulated_separableish_features, labels_onehot, test_size = .1, random_state = 12)

基于Tensorflow构建简单神经网络

输入层，隐藏层（5个神经元）和输出层

#隐含层单元数
hidden_nodes = 5
num_labels = train_labels.shape[1]
#批处理大小
batch_size = 100
num_features = train_dataset.shape[1]
#学习率
learning_rate = .01

graph = tf.Graph()
with graph.as_default():

    # 数据
    tf_train_dataset = tf.placeholder(tf.float32, shape = [None, num_features])
    tf_train_labels = tf.placeholder(tf.float32, shape = [None, num_labels])
    tf_test_dataset = tf.constant(test_dataset)

    # 权重和偏置
    layer1_weights = tf.Variable(tf.truncated_normal([num_features, hidden_nodes]))
    layer1_biases = tf.Variable(tf.zeros([hidden_nodes]))

    layer2_weights = tf.Variable(tf.truncated_normal([hidden_nodes, num_labels]))
    layer2_biases = tf.Variable(tf.zeros([num_labels]))

    # 三层的神经网络
    def three_layer_network(data):
        input_layer = tf.matmul(data, layer1_weights)
        hidden = tf.nn.relu(input_layer + layer1_biases)
        output_layer = tf.matmul(hidden, layer2_weights) + layer2_biases
        return output_layer

    # Model Scores
    model_scores = three_layer_network(tf_train_dataset)

    #损失值
    loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=model_scores, labels=tf_train_labels))

    # 优化器
    optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)

    # 预测
    train_prediction = tf.nn.softmax(model_scores)
    test_prediction = tf.nn.softmax(three_layer_network(tf_test_dataset))

#定义准确率
def accuracy(predictions, labels):
    preds_correct_boolean =  np.argmax(predictions, 1) == np.argmax(labels, 1)
    correct_predictions = np.sum(preds_correct_boolean)
    accuracy = 100.0 * correct_predictions / predictions.shape[0]
    return accuracy

#开始训练
num_steps = 10001

with tf.Session(graph=graph) as session:
    tf.global_variables_initializer().run()
    for step in range(num_steps):
        offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
        minibatch_data = train_dataset[offset:(offset + batch_size), :]
        minibatch_labels = train_labels[offset:(offset + batch_size)]

        feed_dict = {tf_train_dataset : minibatch_data, tf_train_labels : minibatch_labels}

        _, l, predictions = session.run(
            [optimizer, loss, train_prediction], feed_dict = feed_dict
            )

        if step % 1000 == 0:
            print( 'Minibatch loss at step {0}: {1}'.format(step, l))

    print ('Test accuracy: {0}%'.format(accuracy(test_prediction.eval(), test_labels)))

测试集准确率：
Minibatch loss at step 0: 2.359832763671875
Minibatch loss at step 1000: 0.2925601303577423
Minibatch loss at step 2000: 0.17718014121055603
Minibatch loss at step 3000: 0.16064541041851044
Minibatch loss at step 4000: 0.14011278748512268
Minibatch loss at step 5000: 0.12705211341381073
Minibatch loss at step 6000: 0.12798947095870972
Minibatch loss at step 7000: 0.08461454510688782
Minibatch loss at step 8000: 0.07145170122385025
Minibatch loss at step 9000: 0.09841442108154297
Minibatch loss at step 10000: 0.09960160404443741
Test accuracy: 96.4%

为了深入理解神经网络工作原理，选择从头开始构建神经网络不使用Tensorflow直接构建神经网络

1.网络结构

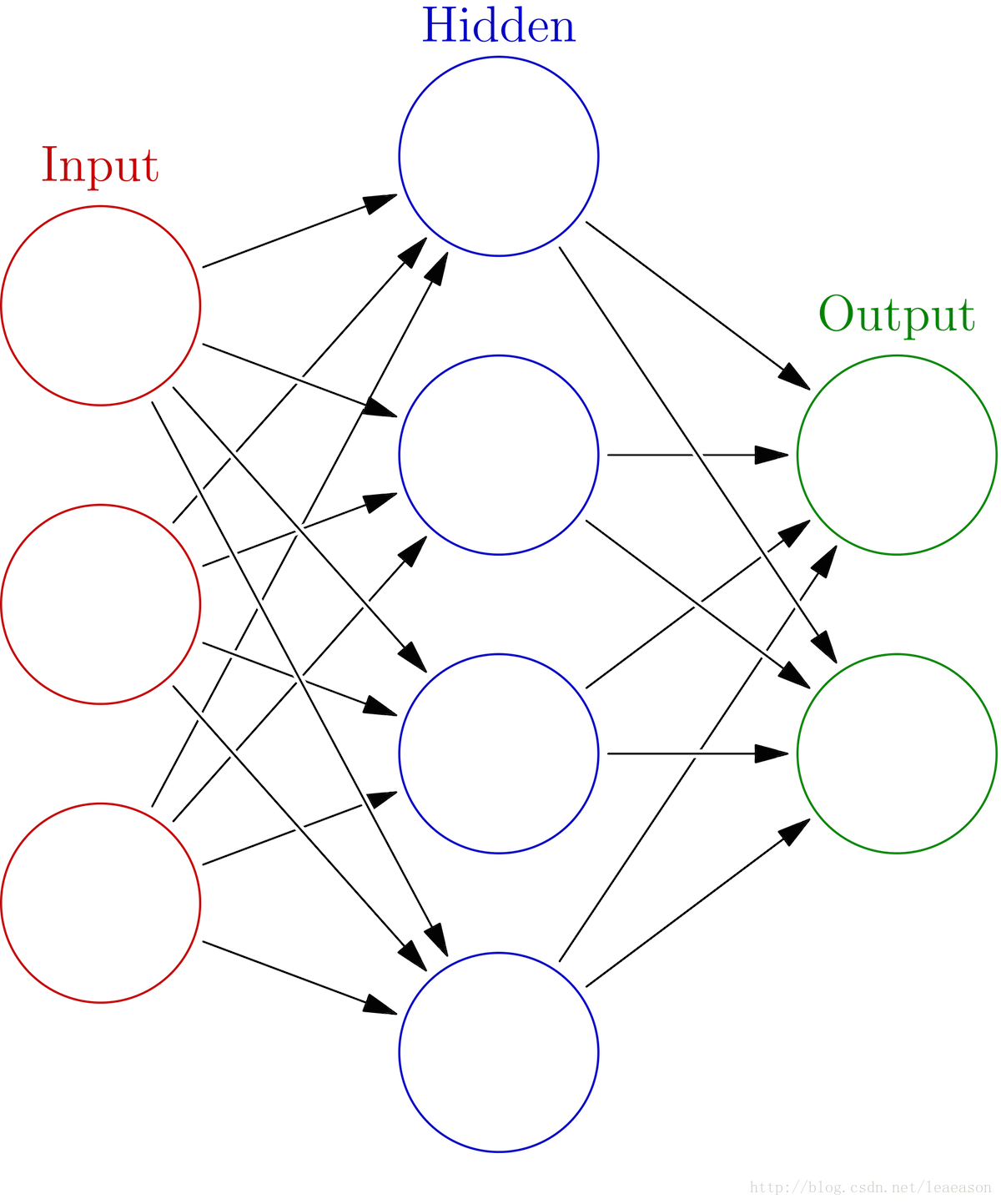
这里写图片描述

2.参数设置以及函数选择

#隐含层单元数
hidden_nodes = 5
num_features = train_dataset.shape[1]
num_labels = train_labels.shape[1]

#初始化权重和偏置
layer1_weights_array = np.random.normal(0, 1, [num_features, hidden_nodes]) 
layer1_biases_array = np.zeros((1, hidden_nodes))

layer2_weights_array = np.random.normal(0, 1, [hidden_nodes, num_labels]) 
layer2_biases_array = np.zeros((1, num_labels))

3.隐含层激活函数
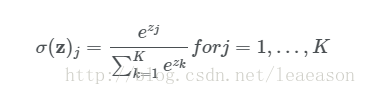
这里写图片描述

#ReLU激活函数 
def relu_activation(data_array):
    return np.maximum(data_array, 0)

4.输出层softmax函数
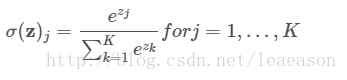
这里写图片描述

def softmax(output_array):
    logits_exp = np.exp(output_array.astype(np.float32))
    return logits_exp / np.sum(logits_exp, axis = 1, keepdims = True)

5.交叉熵损失函数
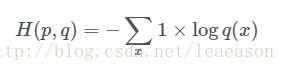
这里写图片描述

def cross_entropy_softmax_loss_array(softmax_probs_array, y_onehot):
    indices = np.argmax(y_onehot, axis = 1).astype(int)
    predicted_probability = softmax_probs_array[np.arange(len(softmax_probs_array)), indices]
    log_preds = np.log(predicted_probability)
    loss = -1.0 * np.sum(log_preds) / len(log_preds)
    return loss

为避免过拟合使用L2正则化

def regularization_L2_softmax_loss(reg_lambda, weight1, weight2):
    weight1_loss = 0.5 * reg_lambda * np.sum(weight1 * weight1)
    weight2_loss = 0.5 * reg_lambda * np.sum(weight2 * weight2)
    return weight1_loss + weight2_loss

3.训练过程以及反向传播中参数的更新

data = train_dataset
labels = train_labels

hidden_nodes = 5
num_labels = labels.shape[1]
num_features = data.shape[1]
learning_rate = .01
reg_lambda = .01

for step in range(5001):

    input_layer = np.dot(data, layer1_weights_array)
    hidden_layer = relu_activation(input_layer + layer1_biases_array)
    output_layer = np.dot(hidden_layer, layer2_weights_array) + layer2_biases_array
    output_probs = softmax(output_layer)

    loss = cross_entropy_softmax_loss_array(output_probs, labels)
    loss += regularization_L2_softmax_loss(reg_lambda, layer1_weights_array, layer2_weights_array)
    #误差反向传播
    output_error_signal = (output_probs - labels) / output_probs.shape[0]

    error_signal_hidden = np.dot(output_error_signal, layer2_weights_array.T) 
    error_signal_hidden[hidden_layer <= 0] = 0
    #计算梯度
    gradient_layer2_weights = np.dot(hidden_layer.T, output_error_signal)
    gradient_layer2_bias = np.sum(output_error_signal, axis = 0, keepdims = True)

    gradient_layer1_weights = np.dot(data.T, error_signal_hidden)
    gradient_layer1_bias = np.sum(error_signal_hidden, axis = 0, keepdims = True)

    gradient_layer2_weights += reg_lambda * layer2_weights_array
    gradient_layer1_weights += reg_lambda * layer1_weights_array
    #权重以及阈值更新
    layer1_weights_array -= learning_rate * gradient_layer1_weights
    layer1_biases_array -= learning_rate * gradient_layer1_bias
    layer2_weights_array -= learning_rate * gradient_layer2_weights
    layer2_biases_array -= learning_rate * gradient_layer2_bias

    if step % 500 == 0:
            print ('Loss at step {0}: {1}'.format(step, loss))

损失值：
Loss at step 0: 4.032443656487327
Loss at step 500: 0.5982357882997374
Loss at step 1000: 0.48772191490059846
Loss at step 1500: 0.42160431744565374
Loss at step 2000: 0.3729775782531113
Loss at step 2500: 0.3371694890407784
Loss at step 3000: 0.3097917830393212
Loss at step 3500: 0.2884371558611799
Loss at step 4000: 0.27115358549993746
Loss at step 4500: 0.2566227146885002
Loss at step 5000: 0.24359782822937304
测试集的准确率：

input_layer = np.dot(test_dataset, layer1_weights_array)
hidden_layer = relu_activation(input_layer + layer1_biases_array)
scores = np.dot(hidden_layer, layer2_weights_array) + layer2_biases_array
probs = softmax(scores)
print (accuracy(probs, test_labels))

95.4666666667

4.预测结果：

labels_flat = np.argmax(test_labels, axis = 1)
predictions = np.argmax(probs, axis = 1)
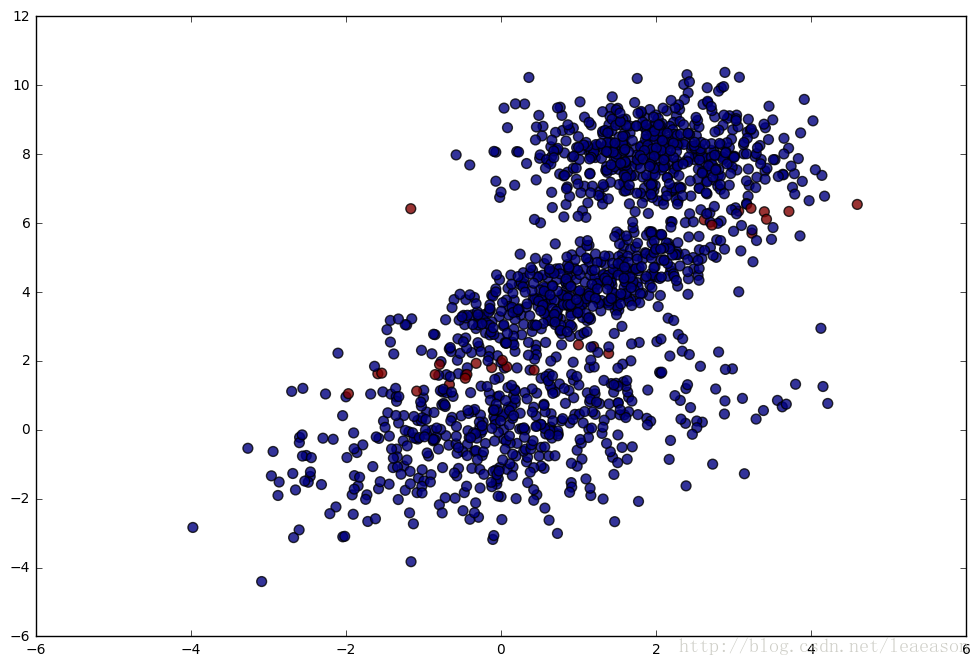
plt.figure(figsize = (12, 8))
plt.scatter(test_dataset[:, 0], test_dataset[:, 1], c = predictions == labels_flat - 1, alpha = .8, s = 50)