【数据结构】优先级队列（堆）1.优先级队列2.优先级队列的模拟实现3.常用接口介绍4.Top-K问题

1.优先级队列

1.1概念

队列是一种先进先出的数据结构。但有些情况下，操作的数据可能带有优先级，一般出队列时，可能需要优先级高的的元素先出队列。这种情况下，数据结构提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象，这种数据结构称之为优先级队列（Priority Queue）

2.优先级队列的模拟实现

JDK1.8中的PriorityQueue底层使用了堆的数据结构，而堆实际就是在完全二叉树的基础之上进行了一些元素的调整。
如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

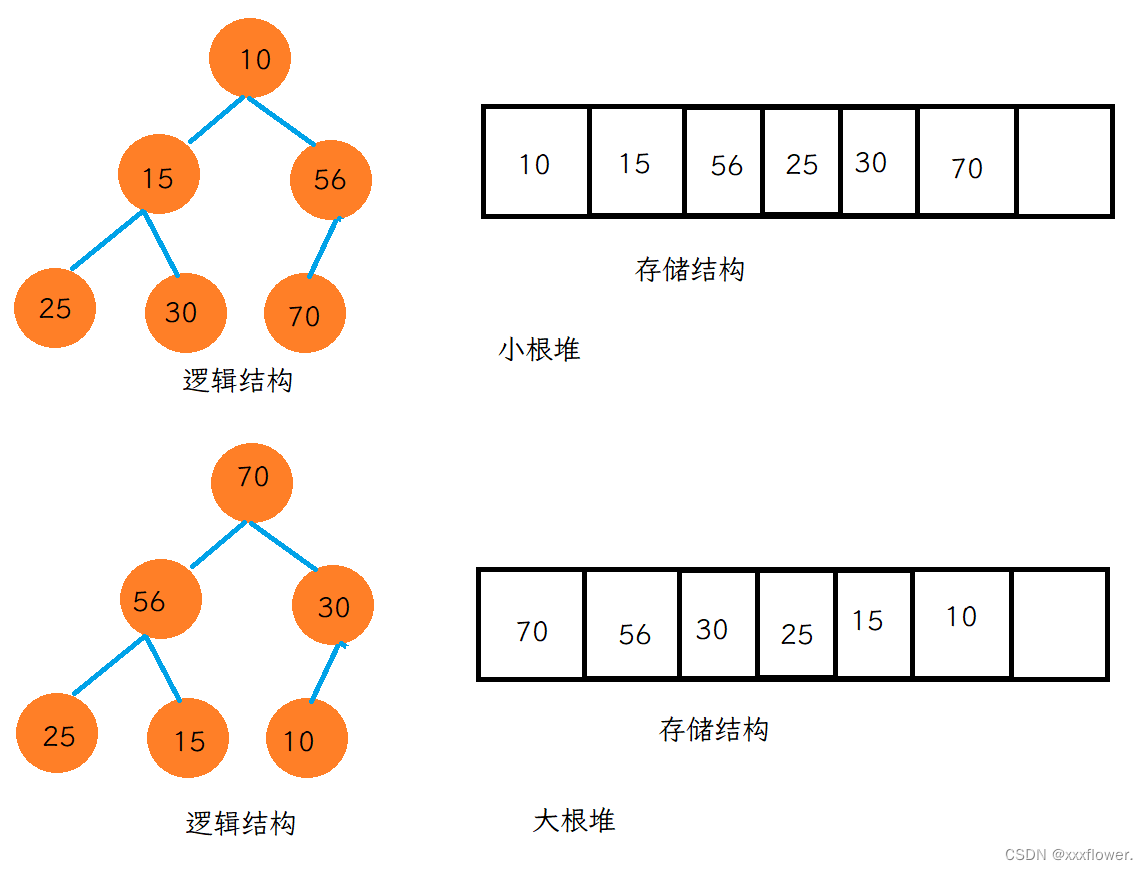
2.1堆的存储方式

堆是一颗完全二叉树，因此可以层序的规则采用顺序的方式来高效存储。

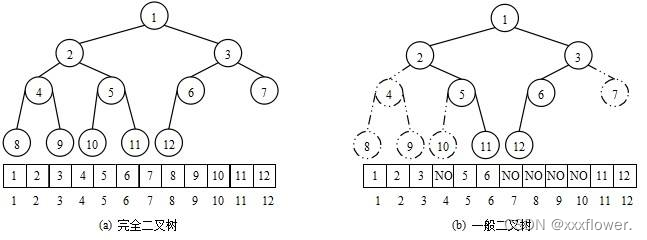
注意：对于非完全二叉树，则不适合使用顺序方式进行存储，因为为了能够还原二叉树，空间中必须要存储空节点，就会导致空间利用率比较低。
将元素存储到数组中后，可以根据二叉树章节的性质5对树进行还原。假设i为节点在数组中的下标，则有：

• 如果i为0，则i表示的节点为根节点，否则i节点的双亲节点为 (i - 1)/2
• 如果2 * i + 1 小于节点个数，则节点i的左孩子下标为2 * i + 1，否则没有左孩子
• 如果2 * i + 2 小于节点个数，则节点i的右孩子下标为2 * i + 2，否则没有右孩子

2.2堆的创建

public class TestHeap {
    public int[] elem;
    public int usedSize;//有效的数据个数
    public static final int DEFAULT_SIZE = 10;
    public TestHeap() {
        elem = new int[DEFAULT_SIZE];
    }
    public void initElem(int[] array){
        for(int i = 0;i < elem.length;i++){
            elem[i] = array[i];
            usedSize++;
        }
    }
    public void createHeap(){
        for(int parent = ((usedSize-1)-1)/2;parent >= 0;parent--){
            shiftdown(parent,usedSize);
        }
    }
    //parent:表示每棵子树的节点
    //len表示没课字数调整的结束位置，不能大于len
    public void shiftdown(int parent,int len){
        int  child= parent * 2 +1;
        //孩子的下标必须小于有效长度，保证有左孩子
        while(child < len){
            //child+1 < len保证有右孩子
            if(child+1 < len && elem[child] < elem[child +1]){
                child ++;
            }
            if(elem[child]>elem[parent]){
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                parent = child;
                child = 2 *parent + 1;
            }else{
                break;
            }
        }
    }
}

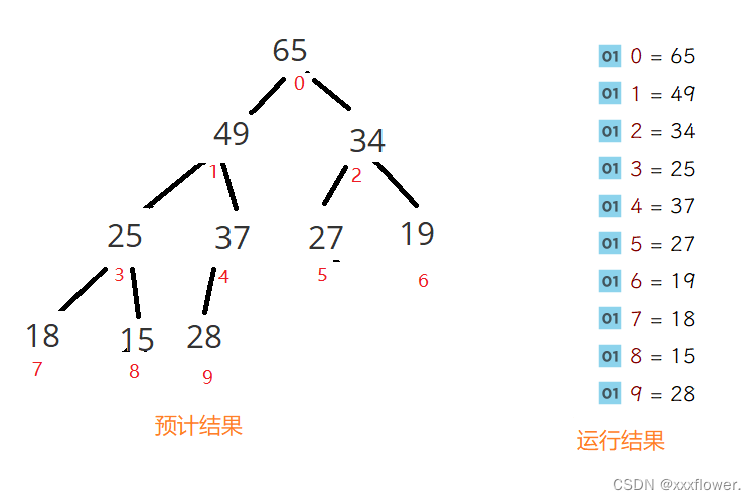
这是大堆的情况下。那么我们如何改为小根堆呢？很简单，只需要改变两个符号。

2.3建堆的复杂度

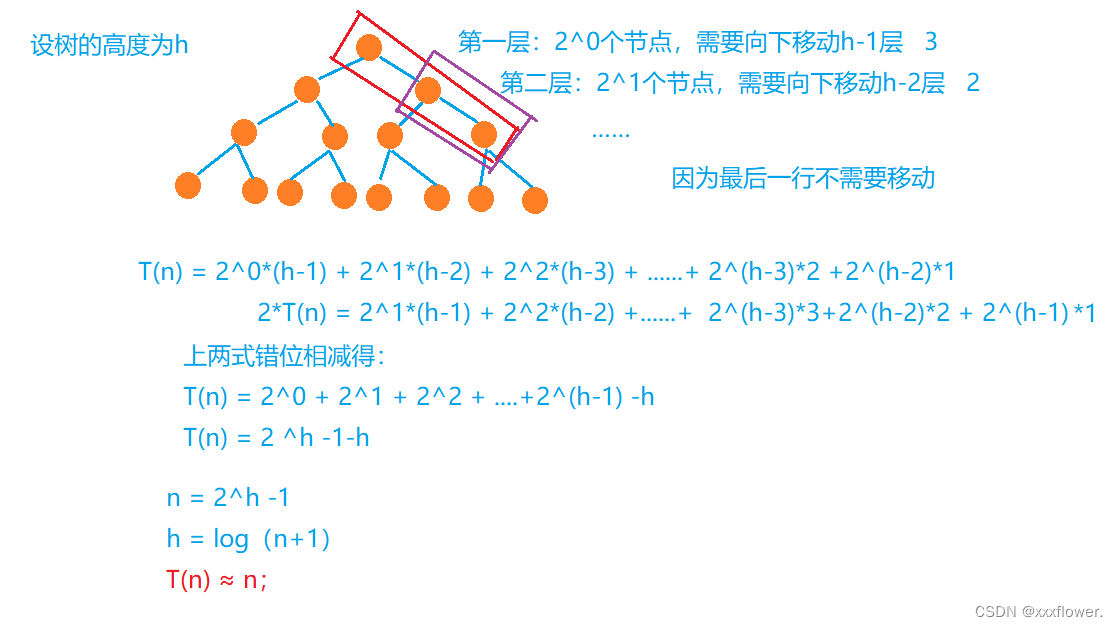
综上：建堆的时间复杂度为O(n)

2.4堆的插入和删除

想要向堆中插入元素，我们可以先插入到最后一个位置上。在对其进行大根堆调整。

public void offer(int val){
        //如果满了就扩容
        if(isFull()){
            elem = Arrays.copyOf(this.elem,2*this.elem.length);
        }
        elem[usedSize] = val;
        usedSize++;
        //调整为大根堆
        shiftup(usedSize-1);
    }
    public void shiftup(int child){
        int parent = (child-1)/2;
        while(parent >= 0){
            if(elem[child] > elem[parent]){
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child -1)/2;
            }else{
                break;
            }
        }
    }
    public boolean isFull(){
        return usedSize == elem.length;
    }

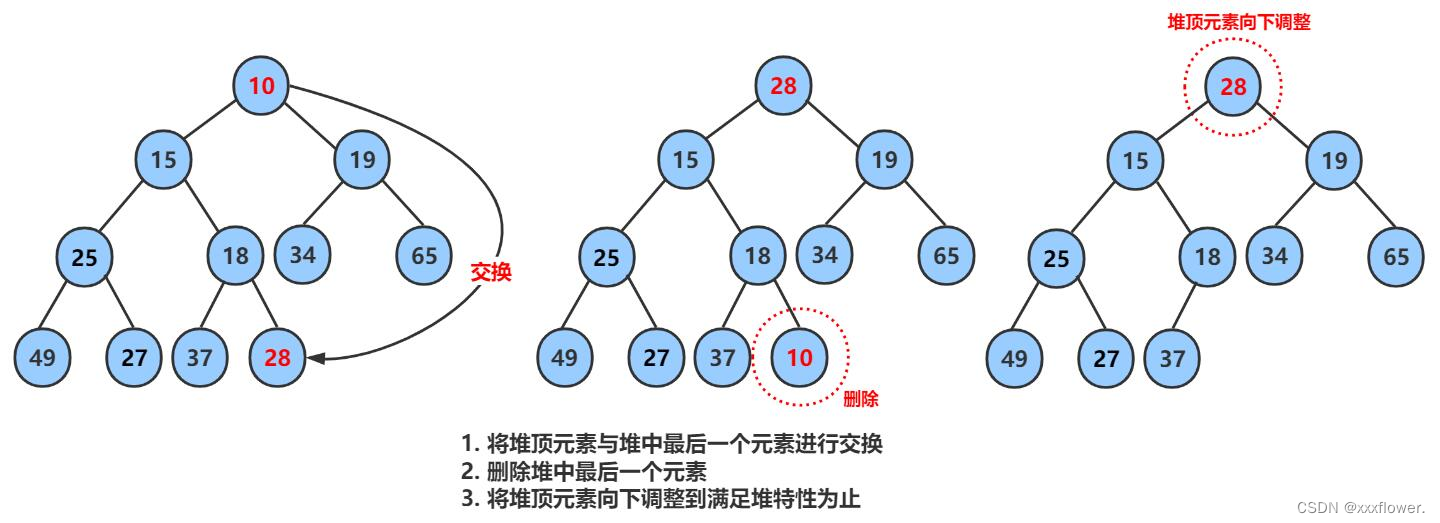
其次，我们来看堆的删除：
堆的删除一定删除的是堆顶元素。（删除中间元素无意义）

public int pop(){
        if(isEmpty()){
            throw new isEmptyExpection("堆空异常!");
        }
        int tmp = elem[0];
        elem[0] = elem[usedSize-1];
        elem[usedSize-1] = tmp;
        usedSize--;
        shiftdown(0,usedSize);
        return tmp;
    }
    public boolean isEmpty(){
        return usedSize == 0;
    }

3.常用接口介绍

Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列，PriorityQueue是线程不安全的，PriorityBlockingQueue是线程安全的。

关于PriorityQueue的使用要注意：

1. 使用时必须导入PriorityQueue所在的包，即：
2. PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出ClassCastException异常
3. 不能插入null对象，否则会抛出NullPointerException
4. 没有容量限制，可以插入任意多个元素，其内部可以自动扩容
5. 插入和删除元素的时间复杂度为
6. PriorityQueue底层使用了堆数据结构
7. PriorityQueue默认情况下是小堆—即每次获取到的元素都是最小的元素
   import java.util.PriorityQueue;
   

默认情况下，PriorityQueue队列是小堆，如果需要大堆需要用户提供比较器；


优先级队列的扩容说明：

1. 如果容量小于64时，是按照oldCapacity的2倍方式扩容的
2. 如果容量大于等于64，是按照oldCapacity的1.5倍方式扩容的
3. 如果容量超过MAX_ARRAY_SIZE，按照MAX_ARRAY_SIZE来进行扩容

4.Top-K问题

题目oj：求数据集合中前k个最大的元素或者最小的元素。
思路一：采用快排，然后写一个循环输出前k项最大/最小的值

public int[] smalllestK(int[] arr,int k){
        Arrays.sort(arr);
        int[] tmp = new int[k];
        for(int i = 0; i< k;i++){
            tmp[i] = arr[i];
        }
        return tmp;
    }

思路二：建一个小根堆，取出数组当中的每个元素，存放到小根堆当中，弹出k个元素，存放到数组当中，返回即可。

public int[] smallestK1(int[] arr,int k){
        //1.建一个堆
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();
        //2.取出数组中的每个元素，存放到小根堆中
        for(int i = 0;i < k;i++){
            minHeap.offer(arr[i]);
        }
        //3.弹出k个元素，存放到数组当中。
        int[] tmp = new int[k];
        for(int i = 0;i < k;i++){
            tmp[i] = arr[i];
        }
        return tmp;
    }

思路三：

Top-K问题：求数据集合中前k个最大的元素或者最小的元素，一般情况下数据量都比较大。

最后

以上就是搞怪铃铛为你收集整理的【数据结构】优先级队列（堆）1.优先级队列2.优先级队列的模拟实现3.常用接口介绍4.Top-K问题的全部内容，希望文章能够帮你解决【数据结构】优先级队列（堆）1.优先级队列2.优先级队列的模拟实现3.常用接口介绍4.Top-K问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。