数据处理(二):数据预处理
这篇文章比较长,大家一定要耐心看下去,并且用代码自己打一遍。相信大家会有收获的
由于数据挖掘中,海量的原始数据有很多不完整,会导致数据挖掘的结果产生偏差。所欲需要对数据进行数据预处理。数据预处理主要包括:
- 数据清洗
- 数据集成
- 数据变换
- 数据规约
1.数据清洗
数据清洗主要是**删除原始数据集中的无关数,重复数据,平滑噪声处理,筛选掉与挖掘主题无关的数据,处理缺失值,异常值等
1.1 缺失值处理
缺失值处理可分为三类:
- 删除记录
- 数据插补
- 不处理
1.1.1 删除数据
当缺失数据的比例在总数据集中只占很小的一部分,可以考虑直接删除该行数据。
1.1.2 数据插补
数据插补常用方法:
| 插补方法 | 方法描述 |
|---|---|
| 均值/中位数/众数插补 | 根据属性值的类型,用该数据取值进行插补 |
| 使用固定值 | 将一个缺失值用一个常量替换,例如北京普通工人的缺失值可以用当年的工人平均标准工资代替 |
| 最近临插补 | 在记录中找到与缺失值最接近的样本的该属性插补 |
| 回归方法 | 根据已有的数据和其他的相关变量的数据建立拟合模型来预测缺失的属性值 |
| 插值法 | 利用已知点建立合适的插值函数发f(x),由未知点求出对应的函数值 |
1.1.3 不处理
一些模型可以将缺失值视为一个特殊的取值,允许直接在有空值的代码上进行建模。
1.2 插值法
主要有拉格朗日插值法,牛顿插值法,还有Hermite插值,分段插值,样条插值等。
1.2.1 拉格朗日插值法
1)根据数学知识可知,对于平面上已知的n个点(无两点在同一条直线上)可以找到一个n-1次多项式
y
=
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
n
−
1
x
n
−
1
y=a_0 + a_1x+a_2x^2 +...+ a_{n-1}x^{n-1}
y=a0+a1x+a2x2+...+an−1xn−1使多项式曲线过这n个点
2)将n个点的坐标
(
x
1
,
y
1
)
(x_1,y_1)
(x1,y1),
(
x
2
,
y
2
)
(x_2,y_2)
(x2,y2)…
(
a
n
−
1
x
n
−
1
)
(a_{n-1}x^{n-1})
(an−1xn−1)带入多项式函数得:
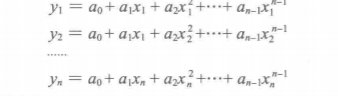
解出拉格朗日插值多项式为:
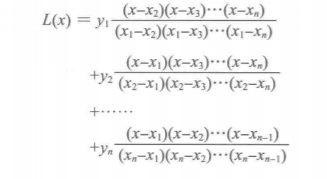
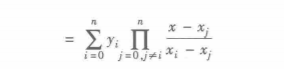
3) 将缺失的函数值对应的点x代入插值多项式得到缺失值的近似值
L
(
x
)
L(x)
L(x)
拉格朗日插值公式结构紧凑,在理论分析中很方便,但当插值点增减时,插值多项式就会随之变化,这在实际运算中很不方便,为了克服这一缺点,提出了牛顿插值法。
1.2.2 牛顿插值法
1)求已知的n个点对
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
.
.
.
(
x
n
,
y
n
)
(x_1,y_1), (x_2,y_2)...(x_n,y_n)
(x1,y1),(x2,y2)...(xn,yn)的所有阶差商公式:
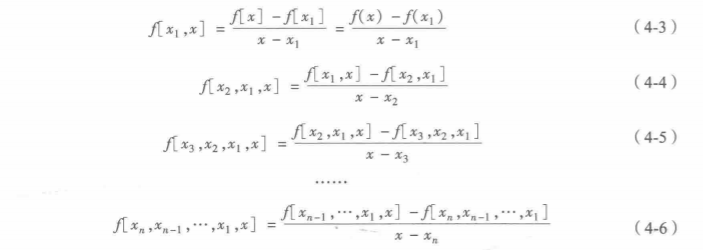
2)联立以上差商公式建立如下插值多项式
f
(
x
)
f(x)
f(x)
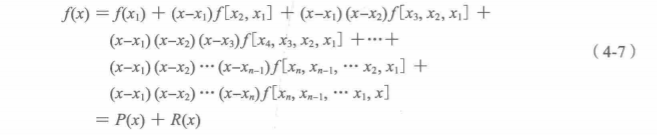
其中:
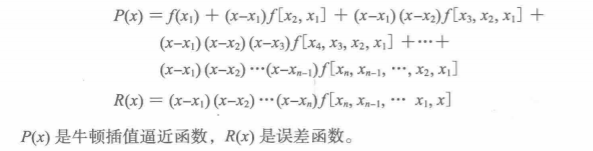
3)将缺失的函数值对应的点x代入插值多项式得到缺失值的近似值
f
(
x
)
f(x)
f(x).
在Python中只提供了拉格朗日插值法的函数,如果需要牛顿插值法,需要自行编写函数.
用python实现牛顿插值法:
| – | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 x 5 x_5 x5 | x 6 x_6 x6 |
|---|---|---|---|---|---|
| x i x_i xi | 0.40 | 0.55 | 0.65 | 0.80 | 0.90 |
| f ( x i ) f(x_i) f(xi) | 0.41075 | 0.57815 | 0.69675 | 0.69675 | 1.02652 |
计算四阶牛顿多项式,并求出f(0.596)
| x i x_i xi | f ( x i ) f(x_i) f(xi) | 一阶商差 | 二阶商差 | 三阶商差 | 四阶商差 | 五阶商差 |
|---|---|---|---|---|---|---|
| 0.40 | 0.41075 | |||||
| 0.55 | 0.57815 | 1.11600 | ||||
| 0.65 | 0.69675 | 1.18600 | 0.28000 | |||
| 0.80 | 0.88811 | 1.27573 | 0.35893 | 0.19733 | ||
| 0.90 | 1.02652 | 1.38410 | 0.43348 | 0.21300 | 0.03134 | |
| 1.05 | 1.25382 | 1.51533 | 0.32493 | 0.22863 | 0.03126 | -0.00012 |
得到:
f
(
x
)
=
0.41075
+
1.11600
(
x
−
0.4
)
+
0.28000
(
x
−
0.4
)
(
x
−
0.55
)
+
0.19733
(
x
−
0.4
)
(
x
−
0.55
)
(
x
−
0.65
)
+
0.03134
(
x
−
0.4
)
(
x
−
0.55
)
(
x
−
0.65
)
(
x
−
0.8
)
f(x)=0.41075+1.11600(x-0.4)+0.28000(x-0.4)(x-0.55)+0.19733(x-0.4)(x-0.55)(x-0.65)+0.03134(x-0.4)(x-0.55)(x-0.65)(x-0.8)
f(x)=0.41075+1.11600(x−0.4)+0.28000(x−0.4)(x−0.55)+0.19733(x−0.4)(x−0.55)(x−0.65)+0.03134(x−0.4)(x−0.55)(x−0.65)(x−0.8)
把0.596代入上式,就可以求出预测值。
import matplotlib.pyplot as plt
from pylab import mpl
import math
"""
牛顿插值法
插值的函数表为
xi 0.4, 0.55, 0.65, 0.80, 0.90, 1.05
f(xi) 0.41075, 0.57815, 0.69675, 0.88811, 1.02652, 1.25382
"""
x = [0.4, 0.55, 0.65, 0.80, 0.90, 1.05]
y = [0.41075, 0.57815, 0.69675, 0.88811, 1.02652, 1.25382]
"""计算五次差商的值"""
def five_order_difference_quotient(x, y):
# i记录计算差商的次数,这里循环5次,计算5次差商。
i = 0
quotient = [0, 0, 0, 0, 0, 0]
while i < 5:
j = 5
while j > i:
if i == 0:
quotient[j]=((y[j]-y[j-1])/(x[j]-x[j-1]))
else:
quotient[j] = (quotient[j]-quotient[j-1])/(x[j]-x[j-1-i])
j -= 1
i += 1
return quotient;
def function(data):
return x[0]+parameters[1]*(data-0.4)+parameters[2]*(data-0.4)*(data-0.55)+parameters[3]*(data-0.4)*(data-0.55)*(data-0.65)+parameters[4]*(data-0.4)*(data-0.55)*(data-0.80)
"""计算插值多项式的值和相应的误差"""
def calculate_data(x,parameters):
returnData=[];
for data in x:
returnData.append(function(data))
return returnData
"""画函数的图像
newData为曲线拟合后的曲线
"""
def draw(newData):
plt.scatter(x,y,label="离散数据",color="red")
plt.plot(x,newData,label="牛顿插值拟合曲线",color="black")
plt.scatter(0.596,function(0.596),label="预测函数点",color="blue")
plt.title("牛顿插值法")
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.legend(loc="upper left")
plt.show()
parameters=five_order_difference_quotient(x,y)
yuanzu=calculate_data(x,parameters)
1.2 异常值处理
在数据预处理得时候,异常值是否剔除,需要根据情况而定。因为有些异常值可能蕴含着许多有用得信息。

将异常值的记录直接删除的方法很简单,但缺陷也很明显。在观测值比较少的情况下,删除异常值是个不明确的选择。可以考虑利用现有的变量信息,对异常值进行填补。
1.3 数据集成
数据挖掘需要的数据往往分布在不同的数据源中,数据集成就是将多个数据源合并并存放在一个一致的数据储存(如数据仓库中)的过程。
需要考虑实体识别的问题和属性冗余问题。
1.3.1 实体识别
实体识别是从不同的数据源识别出现实世界的实体,它的任务是统一不同数据源的矛盾之处。常见形式如下:
(1)同名异义:
数据源A中的属性ID与数据源B中的属性ID分别描述的是菜品编号和订单编号。
(2)异名同义:
义如其名,跟上面相反。
(3)单位不统一:
描述同一实验体可能使用了国际单位和计量单位。
1.3.2 冗余属性识别
数据集成往往导致冗余:
1)同一属性出现多次
2)同一属性名不一致导致重复
有些冗余属性可以用相关性分析检测。
1.4 数据变换
数据变换主要是对数据进行规范化处理。将数据转换成“适当”的形式。
1.4.1 简单函数变换
简单函数变换是对原始数据进行某些数据函数变换,常用的变换包括平方,开方,取对数,差分运算等,即:
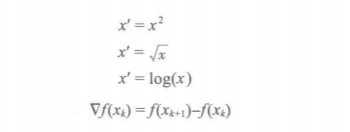
简单的函数变换常用来将不具有正太分布的数据变换成具有正太分布的数据。在时间序列中,有时简单的对数变换或者差分运算就可以将非平稳序列转换成平稳序列。此外,使用对数压缩也是比较常用的方法。
1.4.2 规范化
数据规范化(归一化)处理是数据挖掘的一项基本的工作。不同评价指标往往具有不同的量纲,数值间可能差别很大,不进行处理可能会影响数据分析的结果。为了消除指标之间的量纲和取值范围差异的影响,需要进行标准化处理,将数据按比例进行缩放,使之落入一个特定的区域,比如将工资收入影视到【-1,1】或者【0,1】内
数据规范化对于基于距离的挖掘算法尤为重要。
(1)最小—最大规范化:
最小—最大规范化也称为离差标准化,是对原始数据的线性变换,将数值值映射到[0,1]之间。转换公式如下:
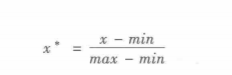
其中,max为样本数据的最大值,min为样本数据的最小值,max-min为极差。离差标准化保留了数据中存在的关系,是消除量纲和数据取值范围影响的最简单的办法。若将来遇到过目前属性[min,max]取值范围的时候,会引起系统错误。
(2) 零—均值规范化
零—均值规范化也成为标准差标准化,经过处理的数据的均值为0,标准差为1,转化公式为:
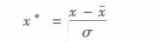
其中σ为原始数据的标准差。是当前用的最多的数据标准化方法。
(3)小数定标规范化
通过移动属性值的小数位数,将属性值映射到[-1,1]之间,移动的小数位数取决于属性绝对值的最大值。转化公式为:
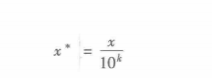
下面通过一个矩阵使用上面3中规范化的处理方法。
#-*- coding: utf-8 -*-
#数据规范化
import pandas as pd
import numpy as np
datafile = '../data/normalization_data.xls' #参数初始化
data = pd.read_excel(datafile, header = None) #读取数据
(data - data.min())/(data.max() - data.min()) #最小-最大规范化
(data - data.mean())/data.std() #零-均值规范化
data/10**np.ceil(np.log10(data.abs().max())) #小数定标规范化
我们看看输出:
>>>data
0 1 2 3
0 78 521 602 2863
1 144 -600 -521 2245
2 95 -457 468 -1283
3 69 596 695 1054
4 190 527 691 2051
>>>(data - data.min())/(data.max() - data.min())
0 1 2 3
0 0.074380 0.937291 0.923520 1.000000
1 0.619835 0.000000 0.000000 0.850941
2 0.214876 0.119565 0.813322 0.000000
3 0.000000 1.000000 1.000000 0.563676
4 1.000000 0.942308 0.996711 0.804149
5 0.264463 0.838629 0.814967 0.909310
6 0.636364 0.846990 0.786184 0.929571
>>>(data - data.mean())/data.std()
0 1 2 3
0 -0.905383 0.635863 0.464531 0.798149
1 0.604678 -1.587675 -2.193167 0.369390
2 -0.516428 -1.304030 0.147406 -2.078279
3 -1.111301 0.784628 0.684625 -0.456906
4 1.657146 0.647765 0.675159 0.234796
5 -0.379150 0.401807 0.152139 0.537286
6 0.650438 0.421642 0.069308 0.595564
>>>data/10**np.ceil(np.log10(data.abs().max()))
0 1 2 3
0 0.078 0.521 0.602 0.2863
1 0.144 -0.600 -0.521 0.2245
2 0.095 -0.457 0.468 -0.1283
3 0.069 0.596 0.695 0.1054
4 0.190 0.527 0.691 0.2051
5 0.101 0.403 0.470 0.2487
6 0.146 0.413 0.435 0.2571
最基础的数据预处理大概就是这些了,希望这些知识对你有所帮助。
最后
以上就是炙热钥匙最近收集整理的关于数据处理(二):数据预处理数据处理(二):数据预处理的全部内容,更多相关数据处理(二)内容请搜索靠谱客的其他文章。








发表评论 取消回复