算法思想：分治法

分治法相关

在偶尔做算法题时，很多人的解题思路都使用了分治法的思想，分治法是一种常用的算法思想。

分治法的核心思想是分解问题，将复杂问题分解，找到问题的最小规模，逐个击破

期间也可以使用递归对分解后的任务进行分治

图解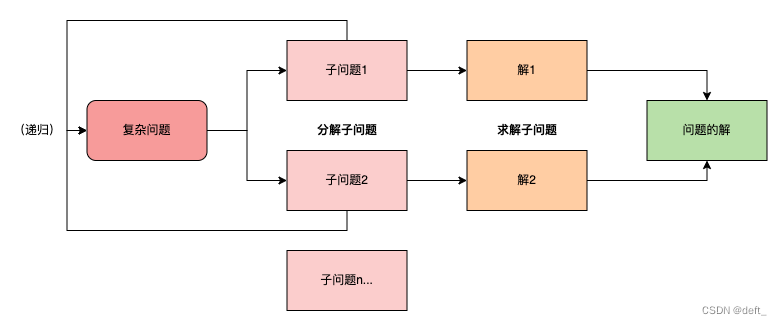

例子：

二分查找：

分治问题最简单的例子即为二分查找，即查找链表的某个值
将链表（数组）分为两个数组（同时对数组进行递归），分别查找两边数组
比较这两个数
以JS为例：

binarySearch(val, arr) {
      const serachFun = (arr, left = 0, right = array.length) => {
        if (left >= right) return -1 // 空 或 头尾相接
        const middle = parseInt((left + right) / 2) // 二分开始
        if (arr[middle] === val) {
          return middle  // 查找成功
        } else if (arr[middle] < val) {
          return serachFun(arr, middle + 1, right) // 移动游标
        } else if (arr[middle] > val) {
          return serachFun(arr, left, middle)   // 移动游标
        }
      }
      const index = serach(arr)
      return index
    }

时间复杂度分析：

根据原理我们可知，设原子个数为n，最大时间复杂度为T(n) （ n > 1 ）

1. 将问题一分为二：T(n/2)
2. 最小原子复杂度为O(n)
   则：
   $$T(n)=T(n/2)+T(n/2)+O(n)=2\cdot T(n/2)+O(n)$$

由此我们即可推出分治-递归的总体时间复杂度

归并排序：

将数组持续地一分为二，递归进行排序，最后依次进行合并
图例：

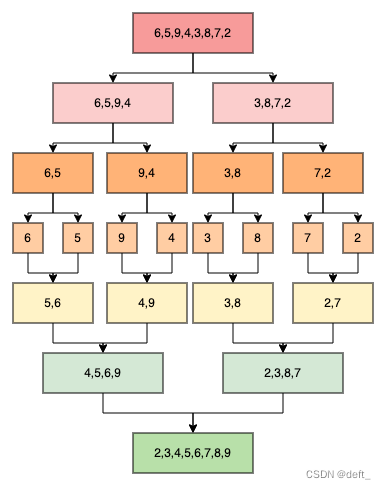
分治-递归时间复杂度：

设：原子个数为n，分解规模为m，最大时间复杂度为T(n) （ m <= n && n > 1 ）
$$T(n)=T(n/m)+T(n/m)+O(n)=m\cdot T(n/m)+O(n)$$

最后

以上就是帅气小兔子为你收集整理的算法思想：分治法的全部内容，希望文章能够帮你解决算法思想：分治法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。