机器学习算法----Adaboost

**

Adaboost算法：

**
设训练数据集T={(x1,y1),(x2,y2)…(xN,yN)}
初始化训练数据的权重分布

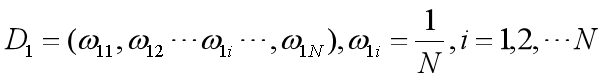
使用具有权值分布Dm的训练数据集学习，得到基本分类器

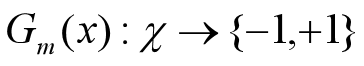
计算Gm(x)在训练数据集上的分类误差率

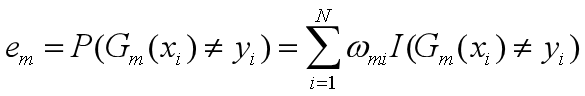
计算Gm(x)的系数

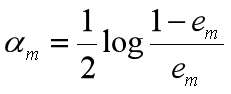
更新训练数据集的权值分布


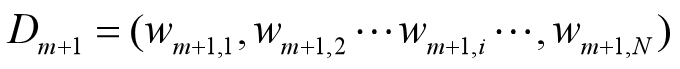
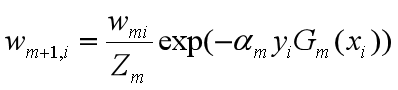
这里，Zm是规范化因子

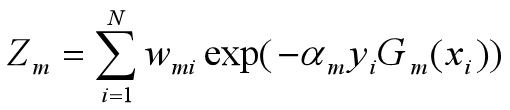
它的目的仅仅是使Dm+1成为一个概率分布

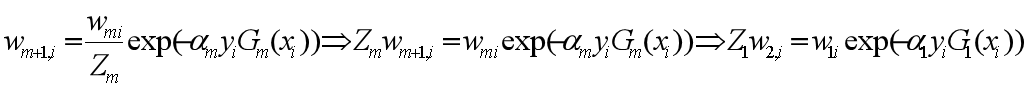
构建基本分类器的线性组合

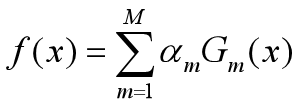
得到最终分类器

**

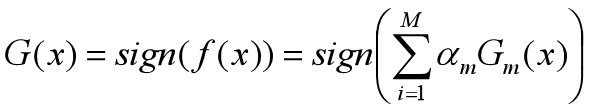
实例

**
•给定下列训练样本，试用AdaBoost算法学习一个强分类器

解：
当m=1时：
•初始化训练数据的权重分布

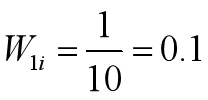
•对于m=1，在权值分布为D1的训练数据上，阈值v取2.5时误差率最低，故基本分类器为：

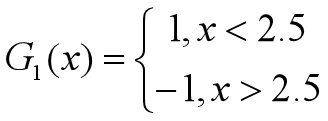
•G1(x)在训练数据集上的误差率为

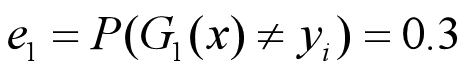
•计算G1的系数

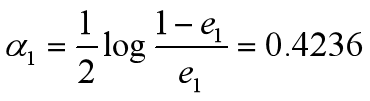
•更新训练数据的权值分布


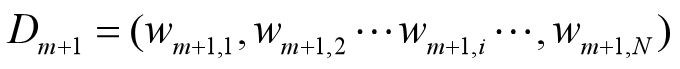
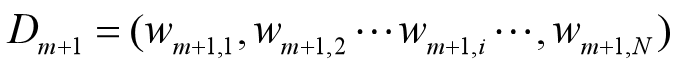
D2={0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715}
分类器为：

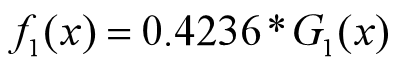
•分类器sign(f1(x))在训练数据集上有3个误分类点。
当m=2时：
•对于m=2，在权值分布为D2的训练数据上，阈值v取8.5时误差率最低，故基本分类器为：

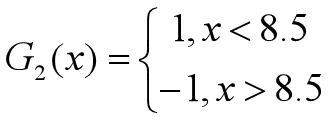
•G2(x)在训练数据集上的误差率为

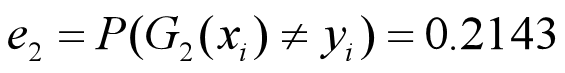
•计算G2的系数

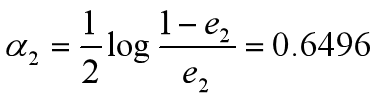
•更新训练数据的权值分布


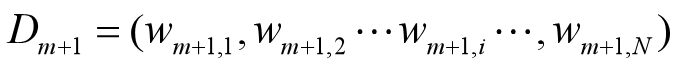
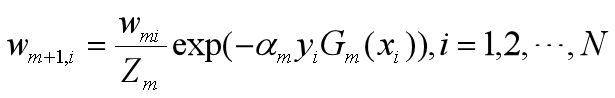
D3={0.0455,0.0455,0.0455,0.1667,0.1667,0.1667,0.1060,0.1060,0.1060,0.1060,0.0455}
分类器为：

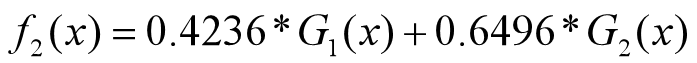
•分类器sign(f2(x))在训练数据集上有3个误分类点。
当m=3时：
•对于m=3，在权值分布为D3的训练数据上，阈值v取5.5时误差率最低，故基本分类器为：

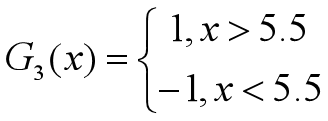
•G3(x)在训练数据集上的误差率为

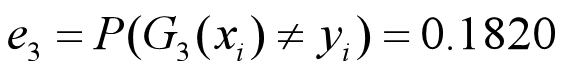
•计算G3的系数

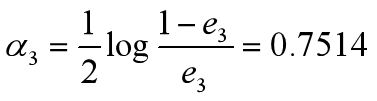
•更新训练数据的权值分布


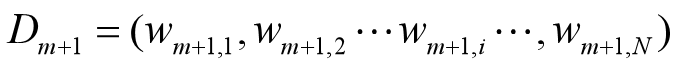
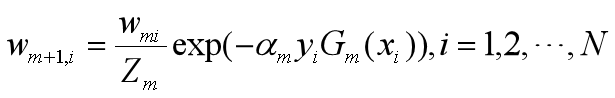
D4={0.125,0.125,0.125,0.102,0.102,0.102,0.065,0.065,0.065,0.125}
分类器为：

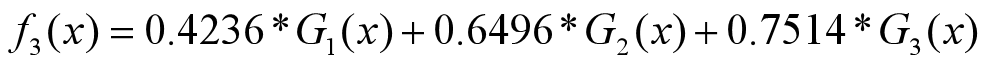
•分类器sign(f3(x))在训练数据集上有0个误分类点。

最后

以上就是文艺可乐最近收集整理的关于机器学习算法----Adaboost的全部内容，更多相关机器学习算法----Adaboost内容请搜索靠谱客的其他文章。