【吴恩达机器学习】学习笔记 （逻辑回归 logistic regression）Logistic Regression

Logistic Regression

前面我们讨论的都是supervised learning中的regression问题，而还有另一类问题叫做classification,这类问题的输出只有0或1，显然就需要用其他方法来解决这类问题。

模型

在线性回归中，我们用h(x)来代表我们的假设函数，这里输出就是我们想要的结果，在逻辑回归里，因为输出项只有0或者1，所以我们需要对这个函数做一下修改，使它产生的输出也是0到1.然后如果h(x)的值大于0.5，代表y为1，h(x)小于0.5，代表y为0.
原来的$$h(x)={\theta }^{T}X$$我们现在利用一个新的函数叫sigmoid function
$$g(z)=\frac{1}{1+e^{-z}}$$
然后得到我们新的h(x)
$$h(x)=g({\theta }^{T}X)$$
这个函数就满足了我们上述的要求，我们也用这个函数来代表逻辑回归中的假设函数

Decision Boundary

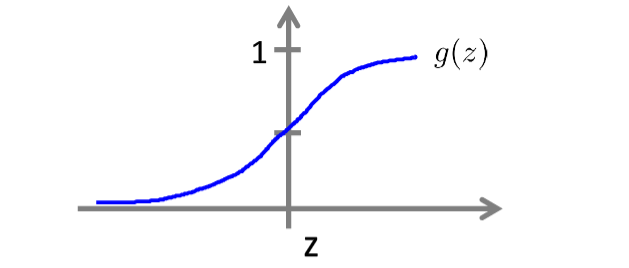
上图是g(z)的图像，如果我们想要最后得到1，即h(x)>0.5,根据图像，我们知道只需让θ^TX>0
例如

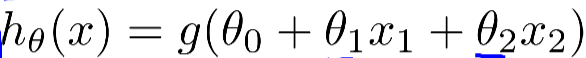
这是我们的h(x),假设θ的三个参数为-3，1，1，那么能得到下面的等式

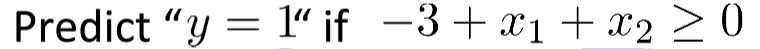
$x1+x2=3$这个等式就叫做decision boundary,它就区分了我们的不同类，如下图

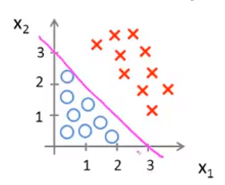
Cost Function

在线性回归中，我们定义的代价函数如下

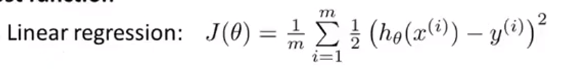
如果我们继续用这个函数来定义逻辑回归的代价函数，就会出现一个问题，这是一个non-convex function，我们不能保证每次求得的是全局最优解，我们需要重新定义一个代价函数


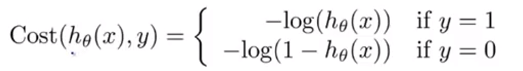
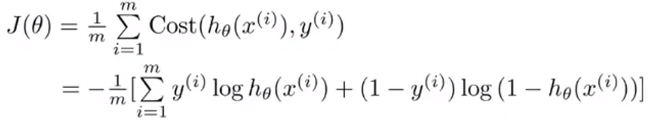
怎么想到这个函数，这里用到了极大似然估计和凸优化，我们只需要记住理解这个函数，这个函数最大的好处就是他是一个凸函数，没有局部最优解。
得到了代价函数，我们就可以用梯度下降的方法求出参数θ。

最后

以上就是忐忑导师为你收集整理的【吴恩达机器学习】学习笔记 （逻辑回归 logistic regression）Logistic Regression的全部内容，希望文章能够帮你解决【吴恩达机器学习】学习笔记 （逻辑回归 logistic regression）Logistic Regression所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。