本文讲解Aurélien Géron所著的《Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow》的第一部分(机器学习基础)的第四章《训练模型》。
该书的总目录如下,分为两部分:第一部分介绍机器学习的基础,第二部分介绍神经网络及深度学习。

到目前为止,我们通常把机器学习模型和训练算法当作黑箱子来处理。如果你实践过前几章的一些示例,你会惊奇地发现你可以优化回归系统,改进数字图像的分类器,甚至可以零基础搭建一个垃圾邮件的分类器,但是你却对它们内部的工作流程一无所知。事实上,许多场合你都不需要知道这些黑箱子的内部有什么,干了什么。
然而,如果你对其内部的工作流程有一定了解的话,当面对一个机器学习任务时候,这些理论可以帮助你快速的找到恰当的机器学习模型,合适的训练算法,以及一个好的超参数集。同时,了解黑箱子内部的构成,有助于你更好地调试参数以及更有效的误差分析。本章讨论的大部分话题对于机器学习模型的理解、构建以及训练神经网络都是非常重要的。
首先,我们将以一个简单的线性回归模型为例,讨论两种不同的训练方法来得到模型的最优解:
i)直接使用封闭方程进行运算,得到模型在当前训练集上的最优参数(即在训练集上使损失函数达到最小值的模型参数)
ii)使用一种叫做梯度下降(GD)的迭代优化方法:在训练集上,它可以逐渐调整模型参数以获得最小的损失函数,最终参数会收敛到和第一种方法相同的的值。同时,我们也会介绍一些梯度下降的变体形式:批量梯度下降(Batch GD)、小批量梯度下降(Mini-batch GD)、随机梯度下降(Stochastic GD),在第二部分的神经网络部分,我们会多次使用它们。
接下来,我们将研究一个更复杂的模型:多项式回归,它可以拟合非线性数据集。由于它比线性模型拥有更多的参数,于是它更容易出现过拟合问题。因此,我们将介绍如何通过学习曲线去判断模型是否出现了过拟合,并介绍几种正则化方法以减少模型出现过拟合的风险。
最后,我们将介绍两个常用于分类的模型:Logistic回归和Softmax回归。
在本章中包含许多数学公式,涉及到一些线性代数和微积分的基本概念。为了理解这些公式,你需要知道什么是向量,什么是矩阵,什么是转置,以及什么是点积,什么是矩阵的逆,什么是偏导数。如果你对这些不是很熟悉的话,你可以阅读本书提供的 Jupyter 在线笔记,它包括了线性代数和微积分的入门指导。对于那些不喜欢数学的人,你也应该快速简单的浏览这些公式。希望它足以帮助你理解大多数的概念。
1)Linear Regression——线性回归
在第一章,我们介绍了一个简单的生活满意度回归模型,这个模型仅仅是输入量GDP_per_capita的线性函数。
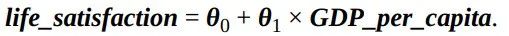
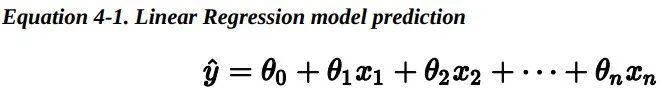
上述公式可以写成更为简洁的向量形式:

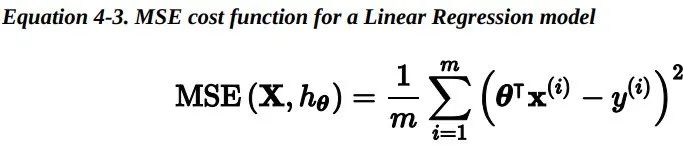
为了找到最小化损失函数的 theta 值,可以采用公式解,换句话说,就是可以通过解正规方程直接得到最后的结果。
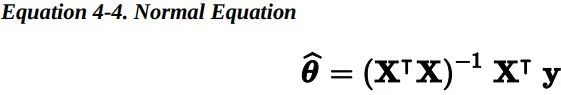
让我们生成一些近似线性的数据来测试一下这个方程。
import numpy as npX = 2 * np.random.rand(100, 1)y = 4 + 3 * X + np.random.randn(100, 1)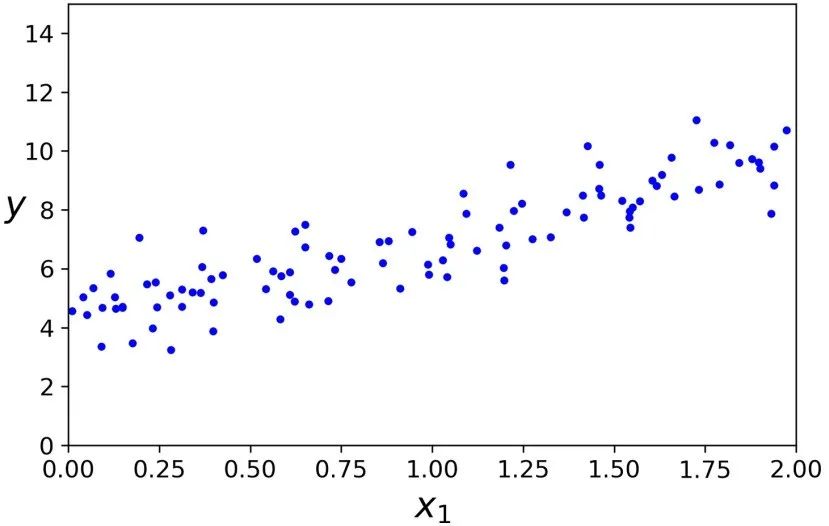
现在让我们使用正规方程来计算 theta,我们将使用 Numpy 的线性代数模块(np.linalg)中的inv()函数来计算矩阵的逆,以及dot()方法来计算矩阵的乘法。X_b = np.c_[np.ones((100, 1)), X] # add x0 = 1 to each instancetheta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
我们生成数据的函数实际上 是 y = 4 + 3x + Gaussian noise 。让我们看一下最后的计算结果。>>> theta_bestarray([[4.21509616], [2.77011339]])>>> X_new = np.array([[0], [2]])>>> X_new_b = np.c_[np.ones((2, 1)), X_new] # add x0 = 1 to each instance>>> y_predict = X_new_b.dot(theta_best)>>> y_predictarray([[4.21509616], [9.75532293]])
画出这个模型的图像。
plt.plot(X_new, y_predict, "r-")plt.plot(X, y, "b.")plt.axis([0, 2, 0, 15])plt.show()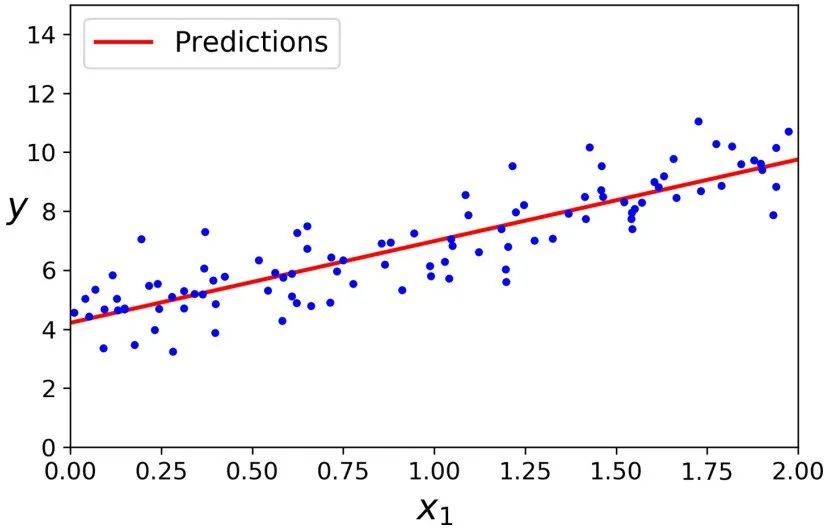
使用 Scikit-Learn 代码执行线性回归模型可以达到相同的效果:
>>> from sklearn.linear_model import LinearRegression>>> lin_reg = LinearRegression()>>> lin_reg.fit(X, y)>>> lin_reg.intercept_, lin_reg.coef_(array([4.21509616]), array([[2.77011339]]))>>> lin_reg.predict(X_new)array([[4.21509616], [9.75532293]])线性回归类是基于scipy.linalg.lstsq()函数的(这个名字代表“最小二乘”),你可以直接调用:
>>> theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)>>> theta_best_svdarray([[4.21509616], [2.77011339]])这个函数其实计算的是x的伪逆与y的乘积,你可以使用np.linalg.pinv()直接计算伪逆:
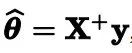
>>> np.linalg.pinv(X_b).dot(y)array([[4.21509616], [2.77011339]])伪逆本身是使用一种称为奇异值分解(SVD)的标准矩阵分解技术来计算的,该技术可以将训练集矩阵X分解成三个矩阵的乘积。
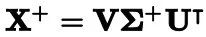
这种方法比计算常规方程更有效,而且它能很好地处理边缘情况:事实上,正规方程可能没法解,如果X.T.dot(X)不可逆的话。例如,当m1.2 Computational Complexity —— 计算复杂度
正规方程需要计算矩阵 X.T.dot(X) 的逆,它是一个(n+1)×(n+1)的矩阵(n是特征的个数)。这样一个矩阵求逆的运算复杂度大约在O(n^2.4) 到O(n^3)之间,具体值取决于实现方式。换句话说,如果你将你的特征个数翻倍的话,其计算时间大概会变为原来的2^2.4=5.3到 2^3=8倍。
Scikit-Learn的线性回归类使用的SVD方法是O (n^2)。如果你将特征的数量加倍,计算时间就会增加大约4倍。
当特征数量增加(如100,000)时,正规方程和SVD方法都会变得非常慢。从积极的一面来看,两者的复杂度对于训练集中的实例数量都是线性的(O(m)),因此它们能够有效地处理大型训练集,只要有内存能存得下这些数据。
同时,一旦你得到了线性回归模型(通过解正规方程或者其他的算法),进行预测是非常快的:因为线性回归的模型计算复杂度对于要进行预测的实例数量和特征个数都是线性的。换句话说,当实例个数变为原来的两倍多的时候(或特征个数变为原来的两倍多),预测时间也仅仅是原来的两倍多。
接下来,我们将介绍另一种方法去训练模型。这种方法适合在特征个数非常多,训练实例非常多,内存无法满足要求的时候使用。
2)Gradient Descent——梯度下降
梯度下降是一种非常通用的优化算法,它能够很好地解决一系列问题。梯度下降的整体思路是通过的迭代来逐渐调整参数使得损失函数达到最小值。假设浓雾下,你迷失在了大山中,你只能感受到自己脚下的坡度。为了最快到达山底,一个最好的方法就是沿着坡度最陡的地方下山。这其实就是梯度下降所做的:它计算误差函数关于参数向量的局部梯度,同时它沿着梯度下降的方向进行迭代。当梯度值为零的时候,就达到了误差函数最小值 。
具体来说,开始时,需要选定一个随机的 theta 值( 这个值称为随机初始值),然后逐渐去改进它,每 一次变化一小步,每一步都试着降低损失函数(例如: 均方差损失函数),直到算法收敛到一个最小值。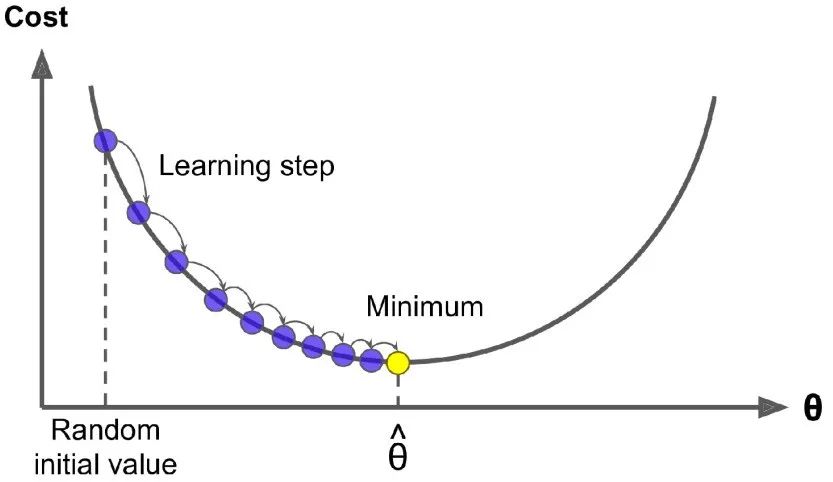
在梯度下降中一个重要的参数是步长,超参数学习率的值决定了步长的大小。如果学习率太小,必须经过多次迭代,算法才能收敛,这是非常耗时的
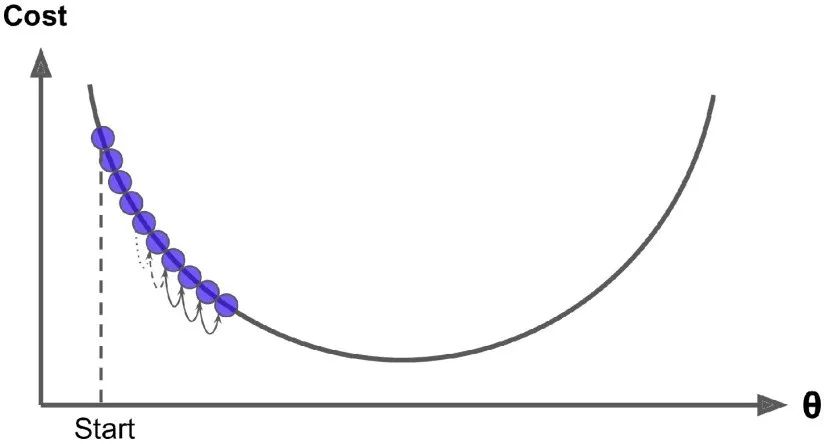
另一方面,如果学习率太大,你将跳过最低点,到达山谷的另一面。这可能使得算法是发散的,损失函数值变得越来越大,永远不可能找到一个好的解。
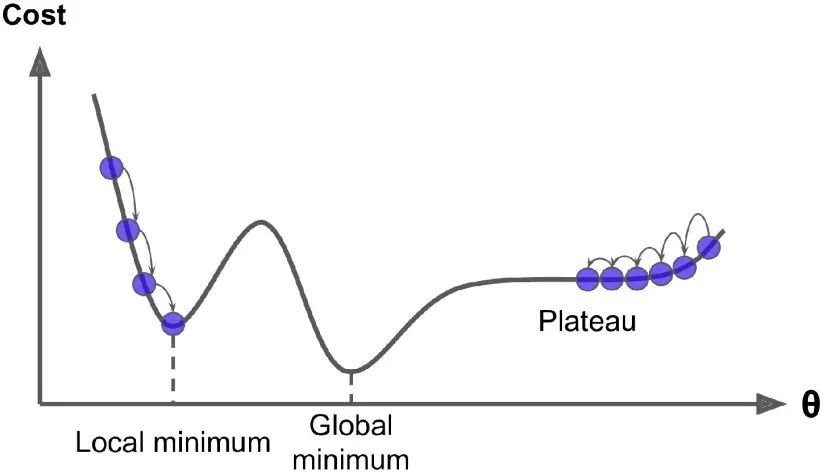
最后,并不是所有的损失函数看起来都像一个规则的碗。它们可能是洞,山脊,平原和各种不规则的地形,使它们收敛到最小值非常困难。如果随机初始值选在了下图图像的左侧,则它将收敛到局部最小值,这个值要比全局最小值要大。如果它从右侧开始,那么跨越高原将需要很长时间,如果你早早地结束训练,你将永远到不了全局最小值。
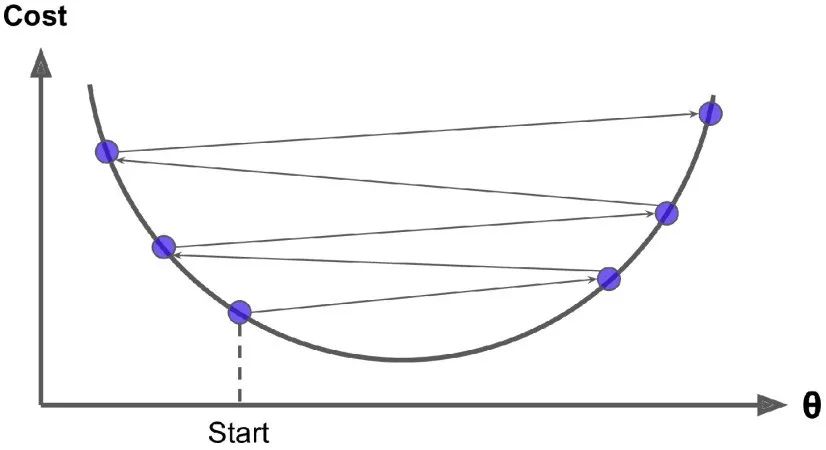
幸运的是,线性回归模型的均方差损失函数是一个凸函数,这意味着如果你选择曲线上的任意两点,它们的连线段不会与曲线发生交叉。这意味着这个损失函数没有局部最小值,仅仅只有一个全局最小值。同时它也是一个斜率不会突变的连续函数。这两个因素导致了一个好的结果:梯度下降可以无限接近全局最小值。(只要你训练时间足够长,同时学习率不是太大 )。
事实上,损失函数的图像呈现碗状,但是不同特征的取值范围相差较大时,这个碗可能是细长的。下图展示了梯度下降在不同训练集上的表现。在左图中,特征 1 和特征 2 有着相同的取值范围。在右图中,特征 1 比特征2的取值要小的多。由于特征 1 较小,因此损失函数改变时,会有较大的变化,于是这个图像会在横轴方向变得细长。
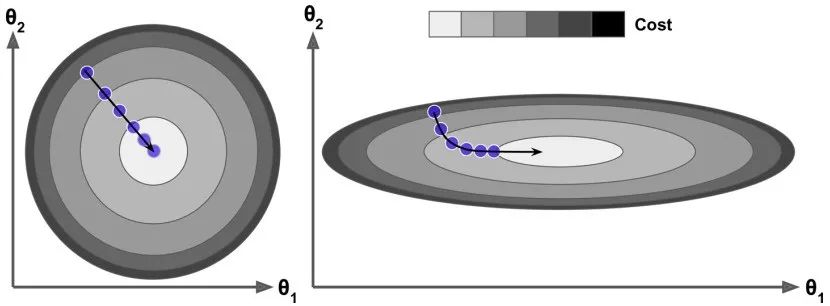
正如你看到的,左面的梯度下降可以直接快速地到达最小值,然而在右面的梯度下降第一次前进的方向几乎和全局最小值的方向垂直,并且最后到达一个几乎平坦的山谷,在平坦的山谷走了很长时间。它最终会达到最小值,但它需要很长时间。
当我们使用梯度下降的时候,应该确保所有的特征有着相近的取值范围(例如:使用 Scikit Learn 的 StandardScaler类),否则它将需要很长的时间才能够收敛。
这幅图也表明了一个事实:训练模型意味着找到一组模型参数,这组参数可以在训练集上使得损失函数最小。这是对于模型参数空间的搜索,模型的参数越多,参数空间的维度越多,找到合适的参数越困难。幸运的是,线性回归模型的损失函数是凸函数,这个最优参数一定在碗的底部。
2.1 Batch Gradient Descent——批梯度下降
使用梯度下降的过程中,你需要计算损失函数关于每一个模型参数的梯度。换句话说,你需要计算当模型参数只变化一点点时,损失函数改变了多少,这称为偏导数。
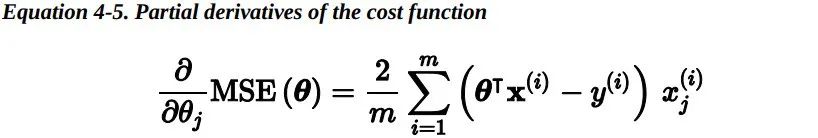

在这个方程中,梯度下降的每一步都计算针对整个训练集进行了计算,这也是为什么这个算法称为批量梯度下降:每一步训练过程都使用所有的的训练数据。因此,在大数据集上,它会变得相当的慢(但是我们接下来将会介绍更快的梯度下降算法)。然而,梯度下降可以很好地扩展到特征特别多的情况中:使用梯度下降训练一个数千个特征的线性回归模型要比使用正规方程或者SVD快得多。
一旦求得了上山方向的梯度向量,你就可以向着相反的方向去下山。这意味着从模型参数中减去偏导数。学习率和梯度向量的积决定了下山时每一步的大小。
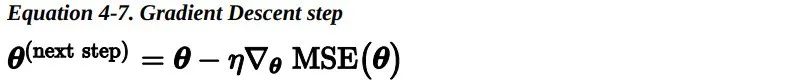
让我们看一下这个算法的实现:
eta = 0.1 # learning raten_iterations = 1000m = 100theta = np.random.randn(2,1) # random initializationfor iteration in range(n_iterations): gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y) theta = theta - eta * gradients这不是太难,让我们看一下最后的结果:
>>> thetaarray([[4.21509616], [2.77011339]])看!这正是正规方程的解。梯度下降完美地求出了参数的最优解。但是当你换一个学习率会发生什么?下图展示了使用了三个不同的学习率进行梯度下降的前 10 步运算(虚线代表起始位置)。
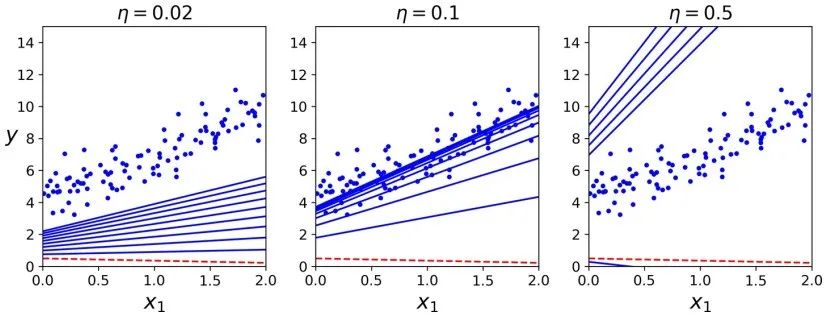
在左面的那副图中,学习率过低:算法最终会达到最优解,但需要很长时间。在中间的这幅图中,学习率看起来不错,仅仅几次迭代后,它就收敛到了最优解。在右面的那副图中,学习率太大了,算法是发散的,每一步都离正确的结果越来越远。
为了找到一个好的学习率,你可以使用网格搜索。当然,你一般会限制迭代的次数,以便网格搜索可以去除需要很长时间才能收敛的模型。
你可能想知道如何选取迭代的次数。如果它太小了,当算法停止的时候,你依然没有找到最优解。如果它太大了,算法会非常的耗时同时迭代参数也不会发生太大的改变。一个简单的解决方法是:设置一个非常大的迭代次数,但是当梯度向量变得非常小的时候,结束迭代。非常小指的是:梯度向量的范数小于一个值e(称为容差)。这时候可以认为梯度下降几乎已经达到了最小值。当损失函数是凸函数,同时它的斜率不会突变(就像均方差损失函数那样),那么固定学习率的批量梯度下降最终将收敛到最优解,但你可能需要等待一段时间:因为它需要O(1/e)次迭代才能达到最优值,这取决于损失函数的形状。换句话说,如果你将容差 缩小 10 倍后(这样可以得到一个更精确的结果),这个算法的迭代次数大约会变成原来的 10 倍。
2.2 Stochastic Gradient Descent —— 随机梯度下降 批量梯度下降的主要问题是每一步计算 梯度时都需要使用整个训练集,这导致在规模较大的数 据集上,其会变得非常的慢。与其完全相反的随机梯度下降,在每一步的梯度计算上只随机选取训练集中的一个样本。很明显,由于每一次的操作都使用了非常少的数据,这样使得算法变得非常快。由于每一次迭代,只需要在内存中有一个实例,这使随机梯度算法可以在大规模训练集上使用。另一方面,由于它的随机性,与批量梯度下降相比,其呈现出更多的不规律性:它到达最小值不是平缓的下降,损失函数会忽高忽低,只是在大体上呈下降趋势。随着时间的推移,它会非常的靠近最小值,但是它不会停止在一个值上,它会一直在这个值附近摆动。因此,当算法停止的时候,最后的参数还不错,但不是最优值。
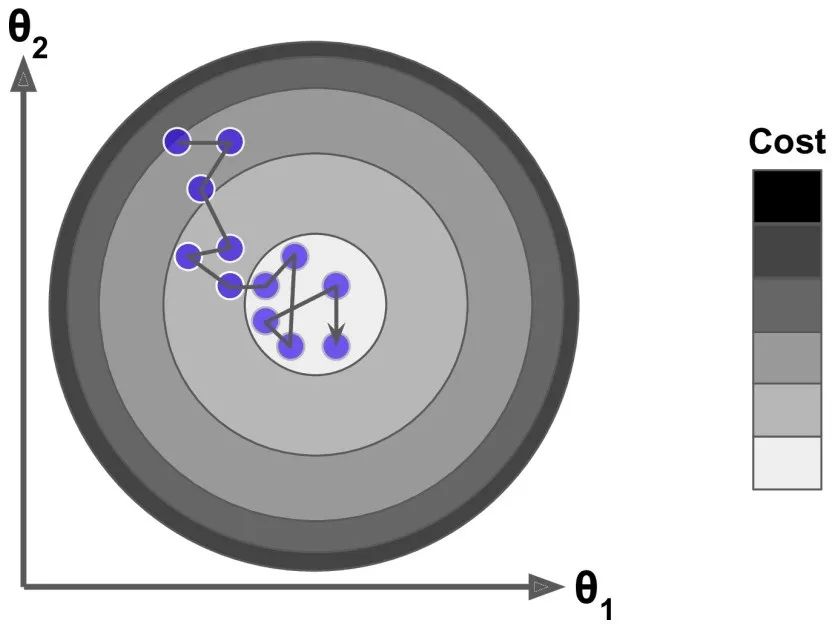
当损失函数很不规则时,随机梯度下降算法能够跳过局部最小值。因此,随机梯度下降在寻找全局最小值上比批量梯度下降表现要好。
虽然随机性可以很好的跳过局部最优值,但同时它却不能达到最小值。解决这个难题的一个办法是逐渐降低学习率。 开始时,走的每一步都较大(这有助于损失函数快速减小同时跳过局部最小值),然后步长变得越来越小,从而使算法到达全局最小值。决定每次迭代的学习率的函数称为learning schedule。 如果学习速度降低得过快,你可能会陷入局部最小值,甚至在到达最小值的半路就停止了。 如果学习速度降低得太慢,你可能在最小值的附近长时间摆动,同时如果过早停止训练,最终只会出现次优解。
下面的代码使用一个简单的learning schedule来实现随机梯度下降:
n_epochs = 50t0, t1 = 5, 50 # learning schedule hyperparametersdef learning_schedule(t): return t0 / (t + t1)theta = np.random.randn(2,1) # random initializationfor epoch in range(n_epochs): for i in range(m): random_index = np.random.randint(m) xi = X_b[random_index:random_index+1] yi = y[random_index:random_index+1] gradients = 2 * xi.T.dot(xi.dot(theta) - yi) eta = learning_schedule(epoch * m + i) theta = theta - eta * gradients按习惯来讲,我们进行 m 轮的迭代。批量梯度下降在整个训练集上迭代了1000次,而随机梯度下降只迭代了50次就得到了一个很好的解:
>>> thetaarray([[4.21076011], [2.74856079]])下图展示了前 20 次的训练过程(注意每一步的不规则程度)。
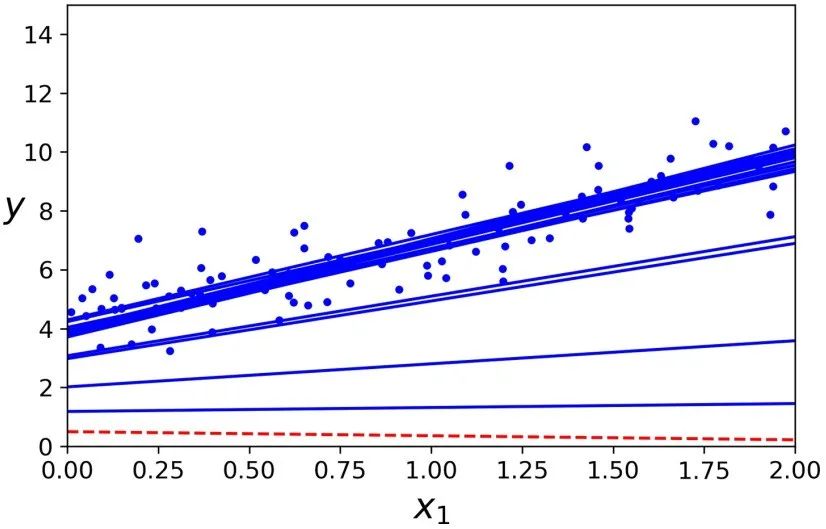
由于每个实例的选择是随机的,有的实例可能一次都没被选到,而有的实例却被多次选到。如果你想保证每一代迭代过程种,算法可以遍历所有实例,一种方法是将训练集打乱重排,然后依次选择一个实例,之后再继续打乱重排,以此类推一直进行下去。但是这样收敛速度会非常的慢。
当使用随机梯度下降时,训练实例必须是独立同分布的(IID),以确保参数从整体上看,是被拉向全局最优的。确保这一点的一个简单方法是在训练期间打乱实例(例如,随机选择每个实例,或在每个epoch开始时打乱训练集)。如果您不打乱样本,例如样本是按标签排序的,那么SGD将首先优化第一个标签,然后优化下一个标签,以此类推,它不会收敛到全局最小值。
通过使用 Scikit-Learn 完成线性回归的随机梯度下降,你需要使用SGDRegressor类,这个类默认优化的是均方差损失函数。下面的代码最大迭代次数为1000或者损失函数的下降值小于0.001(max_iter=1000, tol=1e-3
),学习率 为0.1(eta=0.1),使用默认的learning schedule(与前面的不一样),同时也没有添加任何正则项(penalty = None):
from sklearn.linear_model import SGDRegressorsgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)sgd_reg.fit(X, y.ravel())你可以再一次发现,这个结果非常的接近正规方程的解:
>>> sgd_reg.intercept_, sgd_reg.coef_(array([4.24365286]), array([2.8250878]))最后一个梯度下降算法,我们将介绍小批量梯度下降算法。一旦你理解了批量梯度下降和随机梯度下降,再去理解小批量梯度下降是非常简单的。在迭代的每一步,批量梯度使用整个训练集,随机梯度时候用仅仅一个实例,在小批量梯度下降中,它则使用一个随机的小型实例集。它比随机梯度的主要优点在于你可以通过矩阵运算的硬件优化得到一个较好的训练表现,尤其当你使用 GPU 进行运算的时候。
小批量梯度下降在参数空间上的表现比随机梯度下降要好的多,尤其当小型实例集的规模较大时。因此,小批量梯度下降会比随机梯度更靠近最小值。但是,另一方面,它有可能陷在局部最小值中(在遇到局部最小值问题的情况下,和我们之前看到的线性回归不一样)。下图显示了训练期间三种梯度下降算法在参数空间中的路径。它们都接近最小值,但批量梯度的路径最后停在了最小值,而随机梯度和小批量梯度最后都在最小值附近摆动。但是,不要忘记,批量梯度需要花费大量时间来完成每一步,但是,如果你使用了一个较好的learning schedule,随机梯度和小批量梯度也可以到达最小值。
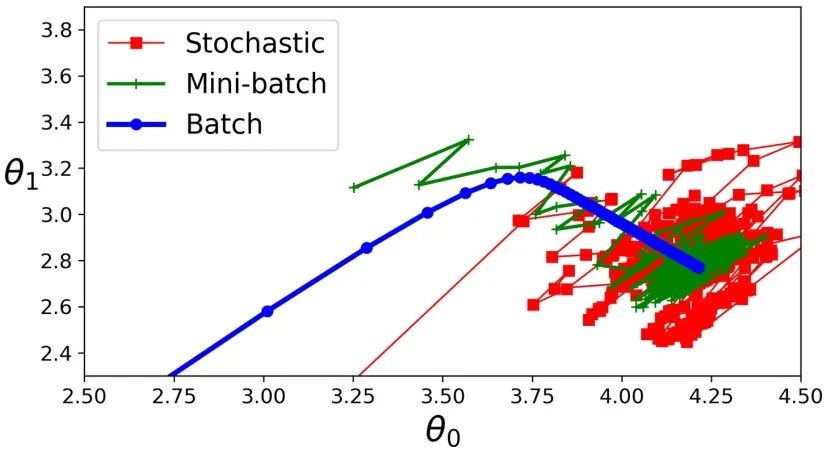
让我们比较一下目前我们已经探讨过的针对线性回归的梯度下降算法。如下表所示。其中,m 表示训练样本的个数,n 表示特征的个数。
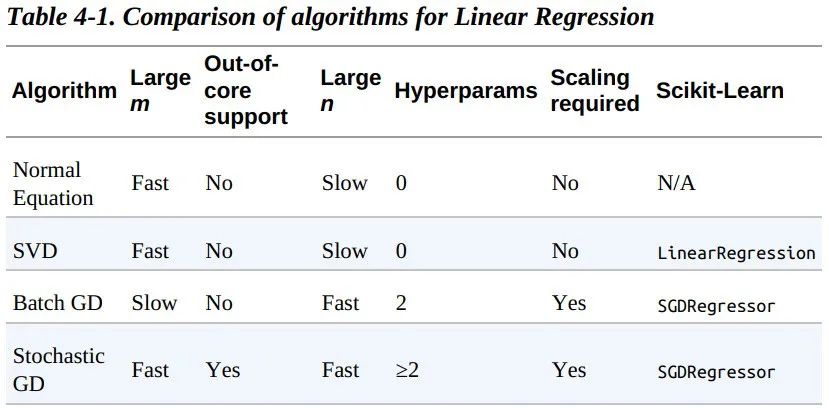

Out-of-core algorithms can handle vast quantities of data that cannot fitin a computer’s main memory. An out-of-core learning algorithm chopsthe data into mini-batches and uses online learning techniques to learnfrom these mini-batches.上述算法在完成训练后,得到的参数基本没什么不同,它们会得到非常相似的模型,最后会以一样的方式去进行预测。
3)Polynomial Regression —— 多项式回归
如果你的数据实际上比简单的直线更复杂呢?令人惊讶的是,你依然可以使用线性模型来拟合非线性数据。一个简单的方法是添加每个特征的幂作为新的特征,然后在这个扩展的特征集上训练一个线性模型。 这种方法称为多项式回归。
让我们看一个例子。首先,我们根据一个简单的二次方程(并加上一些噪声)来生成一些非线性数据:
m = 100X = 6 * np.random.rand(m, 1) - 3y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)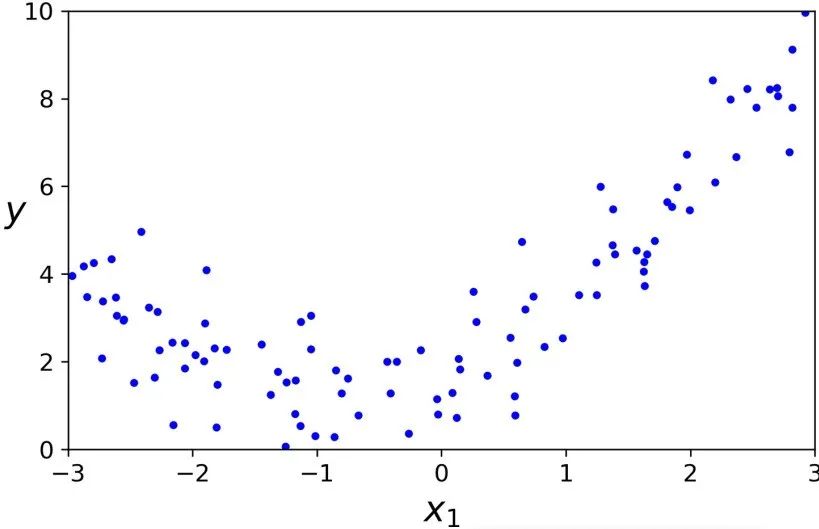
很清楚地可以看出,直线不能恰当的拟合这些数据。于是,我们使用 Scikit-Learning 的PolynomialFeatures类来转换训练数据集,添加训练集中每个特征的平方(2 次多项式)作为新特征:
>>> from sklearn.preprocessing import PolynomialFeatures>>> poly_features = PolynomialFeatures(degree=2, include_bias=False)>>> X_poly = poly_features.fit_transform(X)>>> X[0]array([-0.75275929])>>> X_poly[0]array([-0.75275929, 0.56664654])X_poly现在包含原始特征并加上了这个特征的平方 。现在你可以在这个扩展训练集上使用LinearRegression模型进行拟合:
>>> lin_reg = LinearRegression()>>> lin_reg.fit(X_poly, y)>>> lin_reg.intercept_, lin_reg.coef_(array([1.78134581]), array([[0.93366893, 0.56456263]]))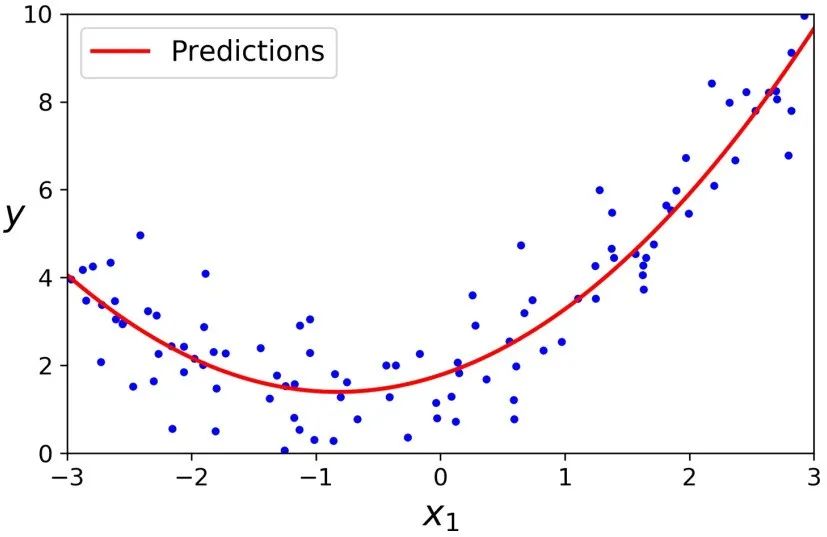
还是不错的。模型预测函数 y_ = 0.56*x^2 + 0.93*x + 1.78,实际上原始函数为 y = 0.5*x^2 + x + 2 + 一些高斯噪声。
请注意,当存在多个特征时,多项式回归能够找出特征之间的关系(这是普通线性回归模型无法做到的)。这是因为PolynomialFeatures 会自动添加给定阶数下特征的所有组合。例如,如果有两个特征 a 和 b ,使用 3 阶( degree=3 )的 PolynomialFeatures 时,不仅有 a^2、a^3、b^2和b^3 , 同时也会有它们的其他组合项 ab、a^2b 和 ab^2 。PolynomialFeatures(degree=d) transforms an array containing n features into an array containing (n+d)!/(n!*d!) features4)Learning Curves —— 学习曲线
如果你使用一个高阶的多项式回归,你可能发现它的拟合程度要比普通的线性回归要好的多。例如,下图使用一个 300 阶的多项式模型去拟合之前的数据集,并同简单线性回归、2 阶的多项式回归进行比较。注意 300 阶的多项式模型如何摆动以尽可能接近训练实例。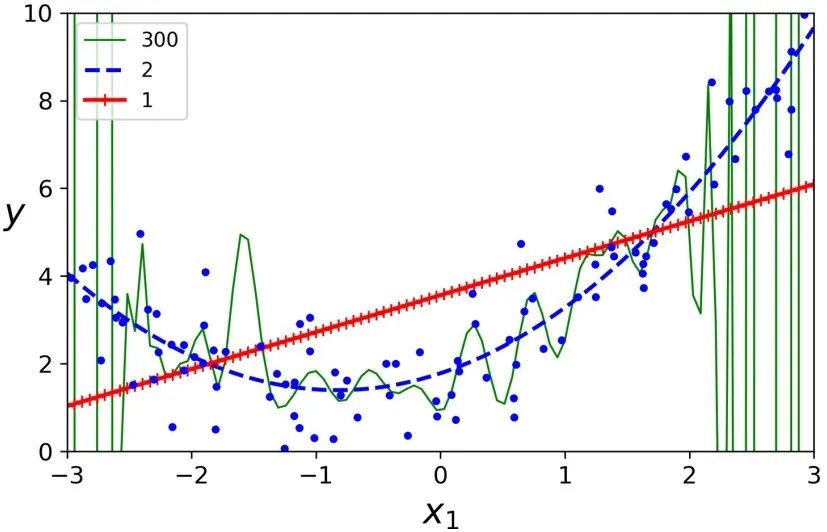
from sklearn.metrics import mean_squared_errorfrom sklearn.model_selection import train_test_splitdef plot_learning_curves(model, X, y): X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2) train_errors, val_errors = [], [] for m in range(1, len(X_train)): model.fit(X_train[:m], y_train[:m]) y_train_predict = model.predict(X_train[:m]) y_val_predict = model.predict(X_val) train_errors.append(mean_squared_error(y_train[:m], y_train_predict)) val_errors.append(mean_squared_error(y_val, y_val_predict)) plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train") plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")lin_reg = LinearRegression()plot_learning_curves(lin_reg, X, y)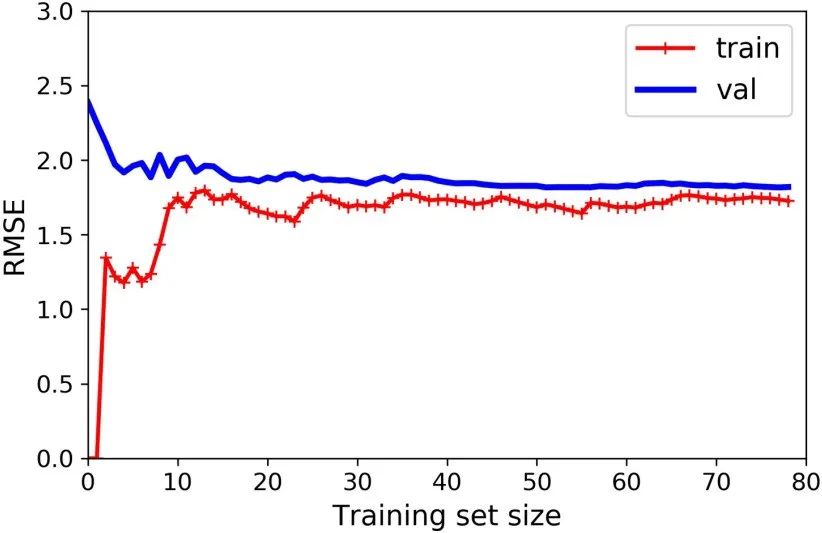
from sklearn.pipeline import Pipelinepolynomial_regression = Pipeline([ ("poly_features", PolynomialFeatures(degree=10, include_bias=False)), ("lin_reg", LinearRegression())])plot_learning_curves(polynomial_regression, X, y)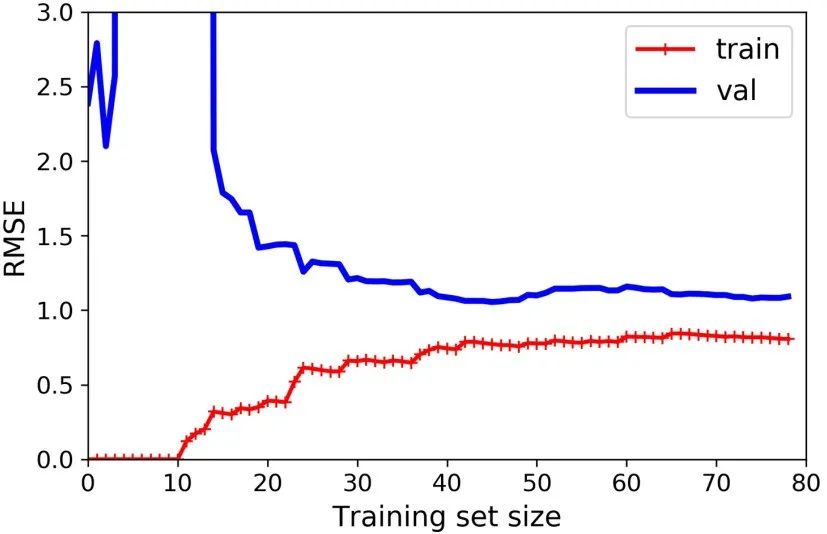
这幅图像和之前的有一点点像,但是其有两个非常重要的不同点:
i) 在训练集上,误差要比线性回归模型低的多。
ii)图中的两条曲线之间有间隔,这意味模型在训练集上的表现要比验证集上好的多,这也是模型过拟合的显著特点。当然,如果你使用了更大的训练数据,这两条曲线最后会非常的接近。
改善模型过拟合的一种方法是提供更多的训练数据,直到训练误差和验证误差相近。偏差和方差的权衡
在统计和机器学习领域有个重要的理论:一个模型的泛化误差由三个不同误差的和决定:
i) 偏差:泛化误差的这部分误差是由于错误的假设决定的。例如实际是一个二次模型,你却假设了一个线性模型。一个高偏差的模型最容易出现欠拟合。
ii) 方差:这部分误差是由于模型对训练数据的微小变化较为敏感,一个多自由度的模型更容易有高的方差(例如一个高阶多项式模型),因此会导致模型过拟合。
iii)不可约误差:这部分误差是由于数据本身的噪声决定的。降低这部分误差的唯一方法就是进行数据清洗(例如:修复数据源,修复坏的传感器,识别和剔除异常值)。
增加模型的复杂性通常会增加其方差并减少其偏差。相反,减少模型的复杂性会增加其偏差并减少其方差。 这就是为什么它被称为一种权衡。5)Regularized Linear Models —— 线性模型的正则化
正如我们在第一和第二章看到的那样,降低模型过拟合的好方法是正则化这个模型(即限制它):模型有越少的自由度,就越难以拟合数据。例如,正则化一个多项式模型,一个简单的方法就是减少多项式的阶数。
对于一个线性模型,正则化的典型实现就是约束模型中参数的权重。接下来我们将介绍三种不同约束权重的方法:Ridge 回归,Lasso 回归和 Elastic Net。
5.1 Ridge Regression —— 岭(Ridge)回归
岭回归(也称为 Tikhonov 正则化)是线性回归的正则化版:在损失函数上直接加上一个正则项
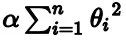
这使得学习算法不仅能够拟合数据,而且能够使模型的参数权重尽量的小。注意到这个正则项只有在训练过程中才会被加到损失函数。当得到完成训练的模型后,我们应该使用没有正则化的测量指标去评价模型的表现。
一般情况下,训练过程使用的损失函数和测试过程使用的评价函数是不一样的。除了正则化,还有一个不同:训练时的损失函数应该在优化过程中易于求导,而在测试过程中,评价函数更应该接近最后的目标。一个好的例子:在分类训练中我们使用对数损失作为损失函数,但是我们却使用精确率/召回率来作为它的评价函数。
超参数 alpha 决定了你想正则化这个模型的强度。如果 alpha=0,那此时的岭回归便变为了线性回归。如果 alpha 非常大,所有权重最后都接近于零,最后结果将是一条穿过数据平均值的水平直线。岭回归的损失函数如下:
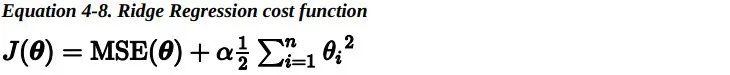
值得注意的是偏差项 theta0 是没有被正则化的(累加运算是从 i=1 而不是 i=0 开始的)。求导后,对于梯度下降来说,仅仅是梯度向量上加上alpha*w这一项 。如果我们定义 w 作为特征的权重向量(theta1 到 theta_n),那么正则项可以简写成 0.5*sqrt(||w||^2),其中 ||w||^2 表示权重向量的 L2 范数。
在使用岭回归前,对数据进行缩放(可以使用StandardScaler)是非常重要的,因为算法对于输入特征的取值范围(scale)非常敏感。大多数的正则化模型都是这样的。
下图展示了在相同线性数据上使用不同 alpha 值的岭回归模型的表现。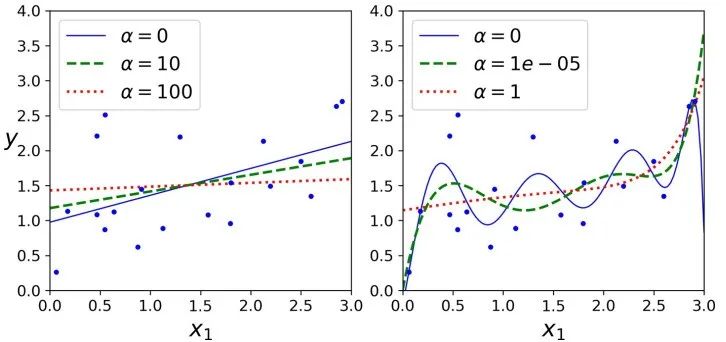
对线性回归来说,对于岭回归,我们可以使用封闭方程去计算,也可以使用梯度下降去处理。它们的缺点和优点同之前所做的分析是一样的。封闭方程的解(矩阵 A 是一个除了左上角有个 0 的单位阵,这个 0 代表偏差项,意味着偏差项 不被正则化)。
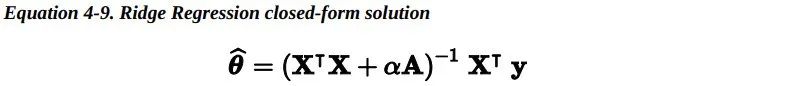
>>> from sklearn.linear_model import Ridge>>> ridge_reg = Ridge(alpha=1, solver="cholesky")>>> ridge_reg.fit(X, y)>>> ridge_reg.predict([[1.5]])array([[1.55071465]])>>> sgd_reg = SGDRegressor(penalty="l2")>>> sgd_reg.fit(X, y.ravel())>>> sgd_reg.predict([[1.5]])array([1.47012588])5.2 LASSO Regression —— LASSO回归
Lasso 回归(也称 Least Absolute Shrinkage and Selection Operator Regression)是另一种正则化版的线性回归:就像岭回归那样,它也在损失函数上添加了一个正则化项,但是它使用权重向量的 L1 范数而不是权重向量 L2 范数平方的一半。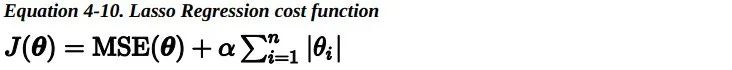
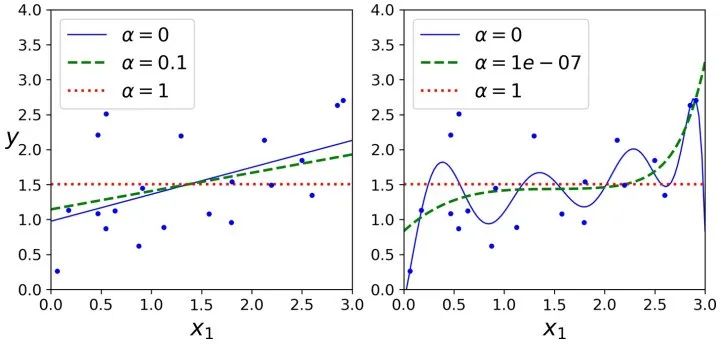
Lasso 回归的一个重要特征是它倾向于完全消除最不重要的特征的权重(即将它们设置为零)。例如,如右图中的虚线所示(alpha=1e-7) ,曲线看起来像一条二次曲线,而且几乎是线性的,这是因为所有的高阶多项式特征的权重都被设置为零。换句话说,Lasso回归自动地进行特征选择同时输出一个稀疏模型(即,具有很少的非零权重)。
你可以从下图知道为什么会出现这种情况。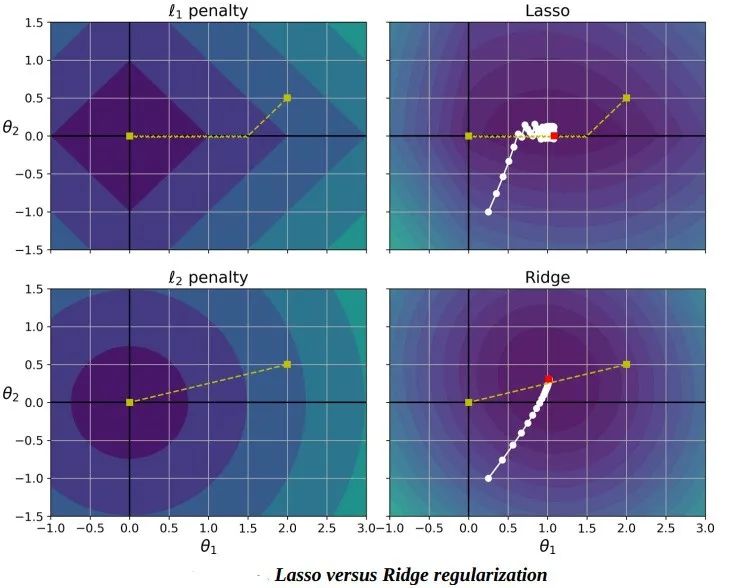
Lasso 损失函数在 theta_i=0 处无法进行微分运算,但是如果你使用子梯度向量,梯度下降仍然起作用。下式是 在 Lasso 损失函数上进行梯度下降的子梯度向量公式。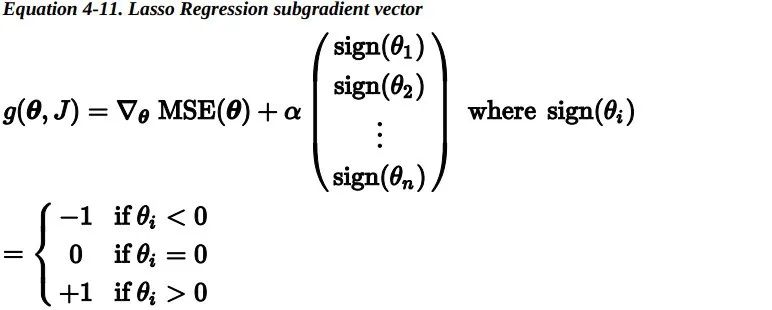
下面是一个使用 Scikit-Learn 的Lasso类的小例子,你也可以使用SGDRegressor(penalty="l1")来代替它。
>>> from sklearn.linear_model import Lasso>>> lasso_reg = Lasso(alpha=0.1)>>> lasso_reg.fit(X, y)>>> lasso_reg.predict([[1.5]])array([1.53788174])
5.3 Elastic Net —— 弹性网
弹性网络介于 Ridge 回归和 Lasso 回归之间。它的正则项是 Ridge 回归和 Lasso 回归正则项的简单混合,同时你可以控制它们的混合率 r。 当 r=0 时,弹性网络就是 Ridge 回归;当 r=1 时,其就是 Lasso 回归。
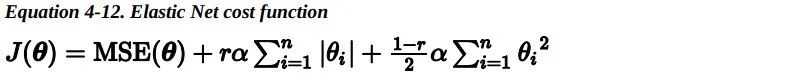
那么我们该如何选择线性回归,岭回归,Lasso 回归或弹性网络呢?一般来说,有一点正则项,模型的表现会更好,因此通常你应该避免使用简单的线性回归。岭回归是一个很好的首选项,但是如果你的特征仅有少数是真正有用的,你应该选择 Lasso 和弹性网络。就像我们讨论的那样,它两能够将无用特征的权重降为零。一般来说,弹性网络的表现要比 Lasso 好,因为当特征数量比样本数量大的时候,或者特征之间有很强的相关性时,Lasso 可能会表现得不规律。下面是一个使用 Scikit-Learn ElasticNet(L1_ratio指的就是混合率 )的简单样本:>>> from sklearn.linear_model import ElasticNet>>> elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)>>> elastic_net.fit(X, y)>>> elastic_net.predict([[1.5]])array([1.54333232])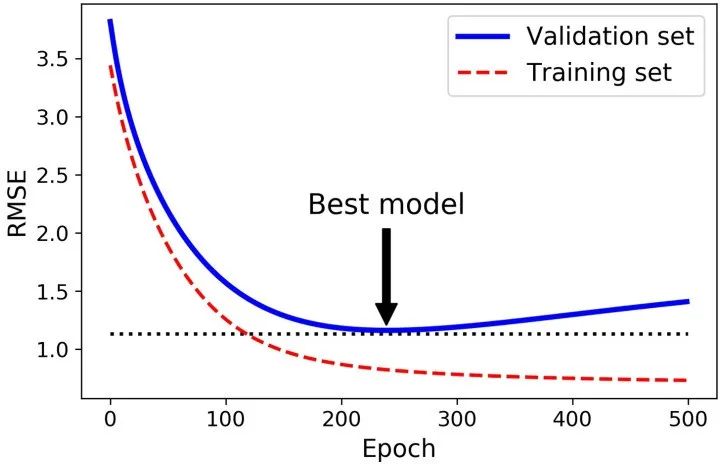
下面是早停的基本实现:
from sklearn.base import clone# prepare the datapoly_scaler = Pipeline([ ("poly_features", PolynomialFeatures(degree=90, include_bias=False)), ("std_scaler", StandardScaler()) ])X_train_poly_scaled = poly_scaler.fit_transform(X_train)X_val_poly_scaled = poly_scaler.transform(X_val)sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True, penalty=None, learning_rate="constant", eta0=0.0005)minimum_val_error = float("inf")best_epoch = Nonebest_model = Nonefor epoch in range(1000): sgd_reg.fit(X_train_poly_scaled, y_train) # continues where it left off y_val_predict = sgd_reg.predict(X_val_poly_scaled) val_error = mean_squared_error(y_val, y_val_predict) if val_error < minimum_val_error: minimum_val_error = val_error best_epoch = epoch best_model = clone(sgd_reg)6)Logistic Regression——逻辑回归
正如我们在第1章中讨论的那样,一些回归算法也可以用于分类(反之亦然)。Logistic 回归(也称为 Logit 回归)通常用于估计一个实例属于某个特定类别的概率(例如,这封电子邮件是垃圾邮件的概率是多少?)。如果估计的概率大于 50%,那么模型预测这个实例属于那个特定类别(称为正类,标记为“1”),反之预测它不属于 那个特定 类别(即它属于负类 ,标记为“0”)。这样便成为了一个二元分类器。 6.1 Estimating Probabilities —— 概率估计那么Logistic 回归是怎样工作的?就像线性回归模型一样,Logistic 回归模型计算输入特征的加权和(加上偏差项),但它不像线性回归模型那样直接输出结果,而是把结果输入logistic()函数进行二次加工后进行输出。
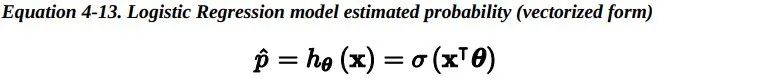
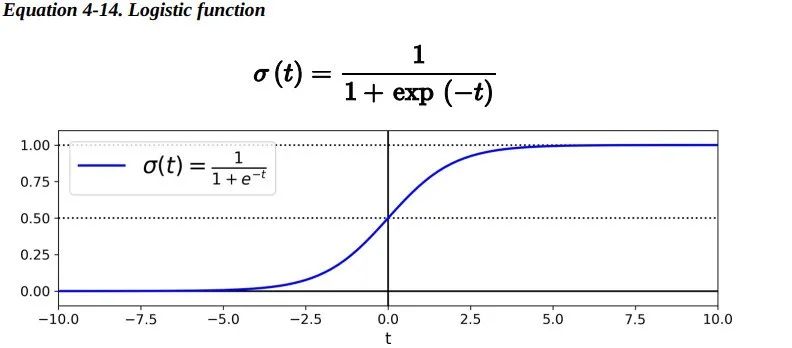
一旦 Logistic 回归模型估计得到了属于正类的概率, 那它很容易做出预测结果。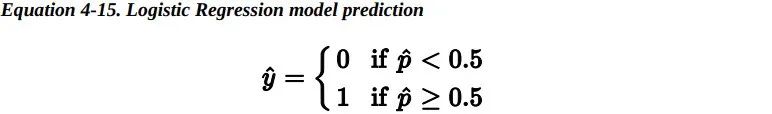
注意:当t<0时,σ(t)<0.5;当t≥0时,σ(t)≥0.5。因此当x^T*theta是正数的的时候,逻辑回归模型输出 1;如果是负数的话,则输出 0。 6.2 Training and Cost Function —— 训练和损失函数好,现在你知道了 Logistic 回归模型如何估计概率并进行预测。但是它是如何训练的呢?训练的目的是调整参数向量theta,使得模型为正类预测较大的概率,为负类预测较小的概率。单个训练实例 的损失函数如下:
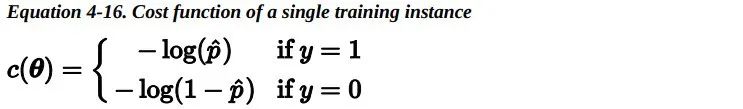
这个损失函数是合理的,因为当 t 接近 0 时,-log(t) 变得非常大,所以如果模型为一个正类估计的概率接近于 0,那么损失函数将会很大;同时如果模型估计一个负类的概率接近 1,那么损失函数同样会很大。另一方面,当 t 接近于 1 时,-log(t) 接近 0,所以如果模型估计一个正类的概率接近于1,那么损失函数接近于 0,同时如果模型估计一个负类的概率接近 0,那么损失函数同样会接近于 0,这正是我们想要的。
整个训练集上的损失函数只是所有训练实例损失的平均值。可以用一个表达式来统一表示,称为对数损失。
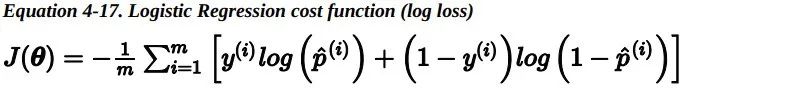
但是对于最小化这个损失函数 是没有闭式解的(没有等价的正规方程 )。但好 消息是,这个损失函数是凸的,所以梯度下降(或任何其他优化算法)一定能够找到全局最小值(如果学习速率不是太大,并且你等待足够长的时间)。下式给出了损失函数关于第 j 个模型参数 theta_j 的偏导数。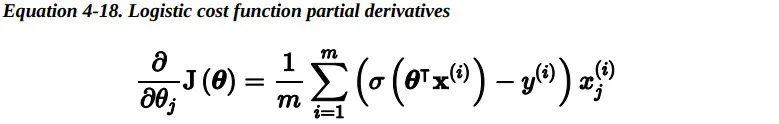

>>> from sklearn import datasets>>> iris = datasets.load_iris()>>> list(iris.keys())['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename']>>> X = iris["data"][:, 3:] # petal width>>> y = (iris["target"] == 2).astype(np.int) # 1 if Iris virginica, else 0from sklearn.linear_model import LogisticRegressionlog_reg = LogisticRegression()log_reg.fit(X, y)X_new = np.linspace(0, 3, 1000).reshape(-1, 1)y_proba = log_reg.predict_proba(X_new)plt.plot(X_new, y_proba[:, 1], "g-", label="Iris virginica")plt.plot(X_new, y_proba[:, 0], "b--", label="Not Iris virginica")# + more Matplotlib code to make the image look pretty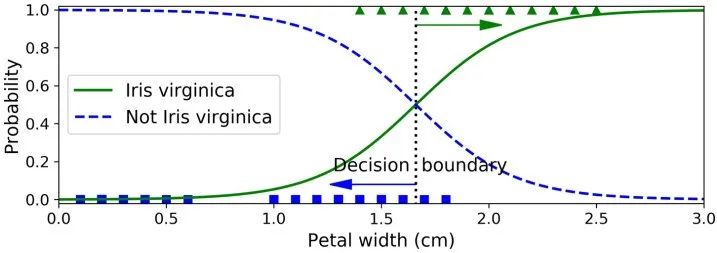
>>> log_reg.predict([[1.7], [1.5]])array([1, 0])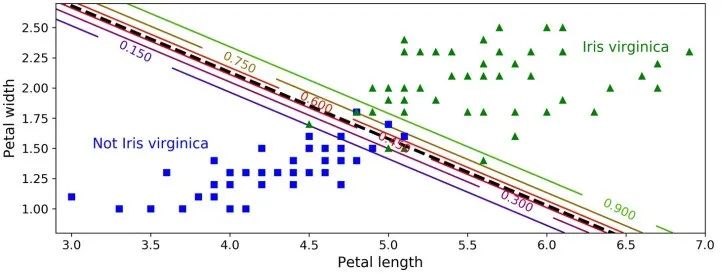
在 Scikit-Learn 的LogisticRegression模型中控制正则化强度的超参数不是 alpha(其它线性模型使用该参数),而是它的逆:C。C 的值越大,模型正则化强度越低。 6.4 Softmax Regression —— Softmax回归 Log istic 回归模型可以 直接推广到支持多类别分类,不必组合和训练多个二分类器 , 称为 Softmax 回归或多项式 Logistic 回归。
这个想法很简单:当给定一个实例x时,Softmax 回归模型首先为第 k 类计算分数s_k(x),然后将Softmax 函数(也称为归一化指数)应用在这些分数上,从而估计出每类的概率。计算s_k(x)的公式看起来很熟悉,因为它就像线性回归预测的公式一样。
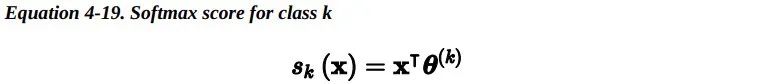
注意,每个类都有自己独一无二的参数向量 theta^(k)。所有这些向量通常作为行放在参数矩阵θ中。
一旦你计算了样本x每一类的得分,你便可以通过Softmax函数估计出样本属于第 k 类的概率:通过计算每个分数的指数,然后再对它们进行归一化(除以所有分数的指数之和)。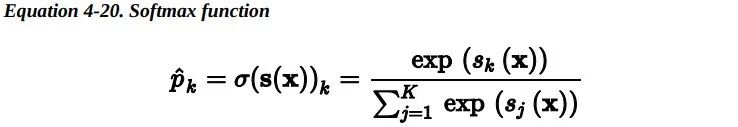
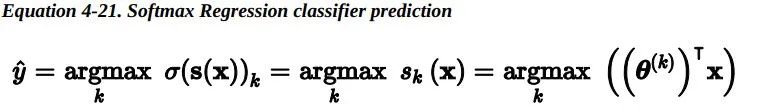
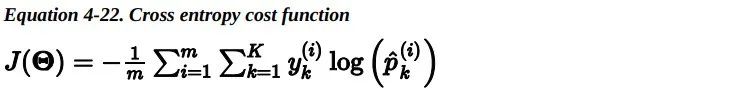
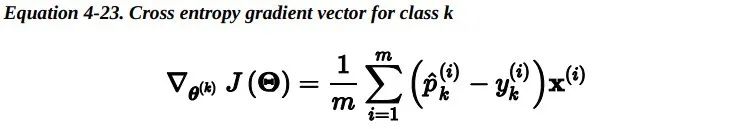
X = iris["data"][:, (2, 3)] # petal length, petal widthy = iris["target"]softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10)softmax_reg.fit(X, y)>>> softmax_reg.predict([[5, 2]])array([2])>>> softmax_reg.predict_proba([[5, 2]])array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])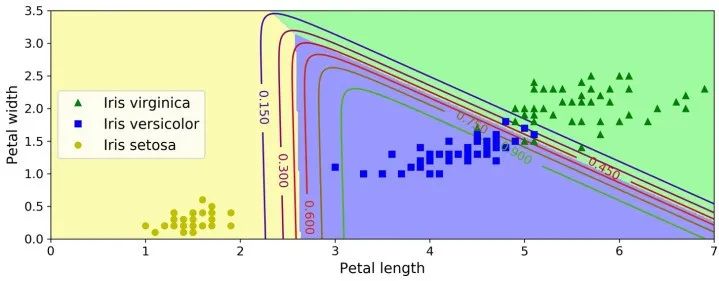
最后
以上就是犹豫耳机最近收集整理的关于基于模型与不基于模型的深度增强学习_基于ScikitLearn、Keras和TensorFlow的机器学习实战:训练模型...的全部内容,更多相关基于模型与不基于模型内容请搜索靠谱客的其他文章。








发表评论 取消回复