枚举
基于逐个尝试答案的一种问题求解策略。
1、例如:求小于N的最大素数
- 找不到一个数学公式,使得根据N就可以直接计算出这个最大素数。
- N-1是素数吗?
- N-2是素数吗?
- …
-> 判断N-i是否为素数的问题
-> 转化为求小于N的全部素数(可以用筛选法)
【C++实现】
#include <iostream>
#include <math.h>
using namespace std;
bool is_preNum(int Num) {
for (int i = 2; i <= sqrt(Num); i++){
if (Num%i == 0){
return false;
}
}
return true;
}
int main()
{
int N;
cout<< "Please Input a int Num(>=2):" << endl;
cin >> N;
if (N < 2) {
cout << "Error Num" << endl;
return 0;
}
for (int i = N - 1; i >=2; i--) {
if (is_preNum(i)) {
cout << "The max prenum is :" << i << endl;
break;
}
}
system("pause");
return 0;
}
2、“完美立方”


解题思路:
四重循环枚举a, b, c, d, 且a 在最外层,d 在最里层,每一层都是从小打到枚举,
- a 的枚举范围是A[2, N]
- b 的枚举范围是B[2, a-1 ]
- c 的枚举范围是C[b, a-1]
- d 的枚举范围是D[c, a-1]
合理的选取枚举范围,能减少不必要的运算。
#include <iostream>
#include <time.h>
using namespace std;
int main()
{
int N;
double start, stop;
start = clock();
std::cin >> N;
start = clock();
for (int a = 2; a <= N; ++a) { //枚举a∈[2,N]
for (int b = 2; b < a; ++b) { //对于每一个a,枚举b∈[2,a-1]
for (int c = b; c < a; ++c) { //对于每一个a和b,枚举c∈[b,a-1]
for (int d = c; d < a; ++d) { //对于每一个abc,枚举d∈[c,a-1]
if (a*a*a == b * b*b + c * c*c + d * d*d) //若枚举出一组数据满足要求,则打印输出
std::cout << "Cude=" << a << 't' << "Triple=" << b << 't' << c << 't' << d << endl;
}
}
}
}
stop = clock();
double duration = (stop - start) / CLK_TCK; //To calculate the time that this function used
std::cout << stop - start <<'t'<<duration << endl;
system("pause"); //Check results
return 0;
}
3、“生理周期”



简单的尝试思路,就是可以对d+1开始直到21252天,每天尝试是否是23、28、33的倍数,但是这样尝试需要遍历20000多次,如图,我们该怎么提高枚举效率

我们知道三天同时出现高峰期时必须是体力的高峰期,所以我们首先找体力的高峰期,即每23天一个循环,再找体力高峰期出现的日子里是不是情商的高峰期,即是不是每28天一个循环,差为28的倍数,如果是则证明即时体力的高峰期又是情商的高峰期,接下来就判断是不是智商的高峰期,即差是不是33的倍数;否则,加23,移到下一个体力的高峰期,直到找到一个体力和情商的双高峰期,然后判断智商的高峰期。智商同理,如果不是智商的高峰期,则需要移到下一个体力和情商的高峰期,加2328;否则输出,即三个的高峰期。
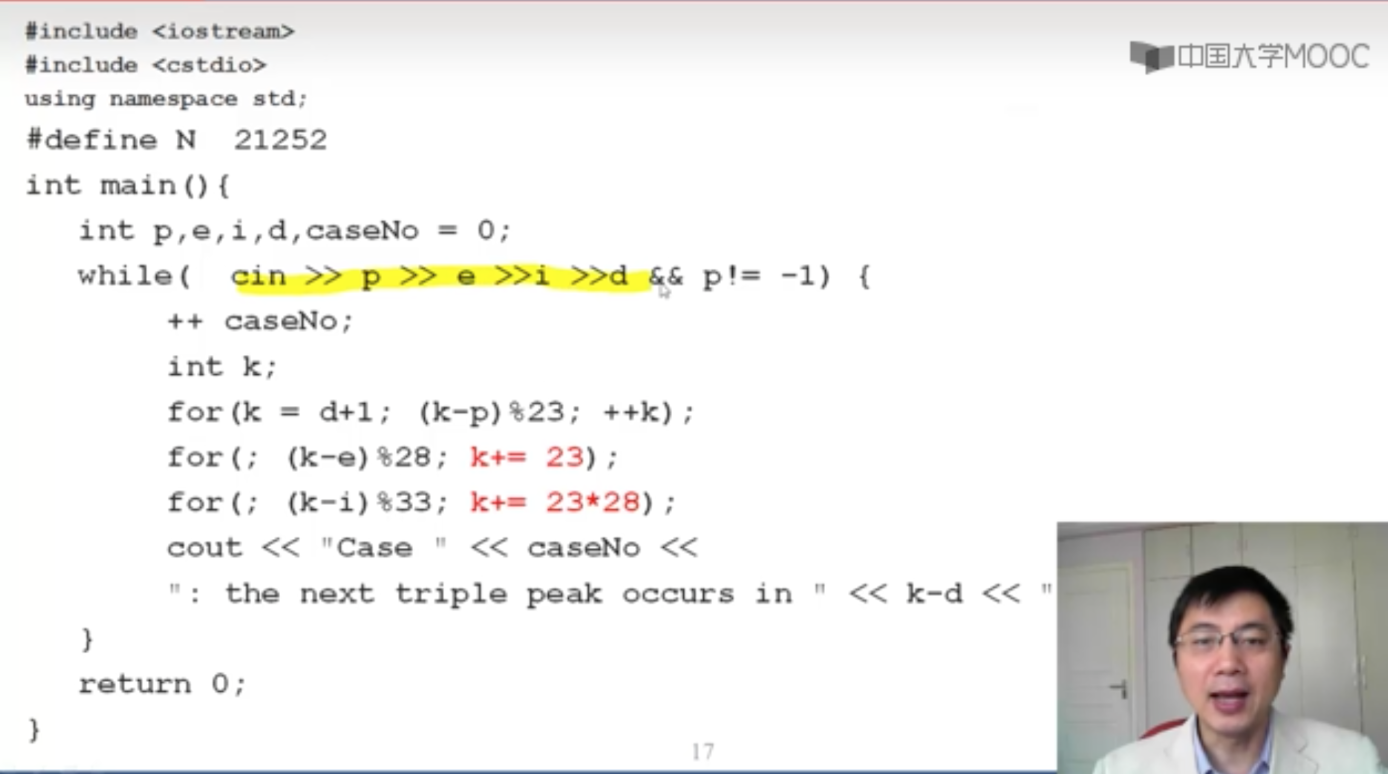
优化算法,只有在体力高峰期的时候才需要判断是不是情商的高峰期,即每隔23天判断情商高峰期,如果是情商高峰期,则判断智商高峰期,如果不是智商高峰期,则每隔2328即体力和情商双高峰期时才判断体力高峰期。
3、称硬币
给出称的结果前提下找真假币,并判断假币轻还是重,不是计算算法称真假币

这道题我们可以枚举从A开始逐个假设是假币并假设轻、重,即如下图,对于A-L,分别假设轻、重并调用函数进行判断此时这种情况是否成立
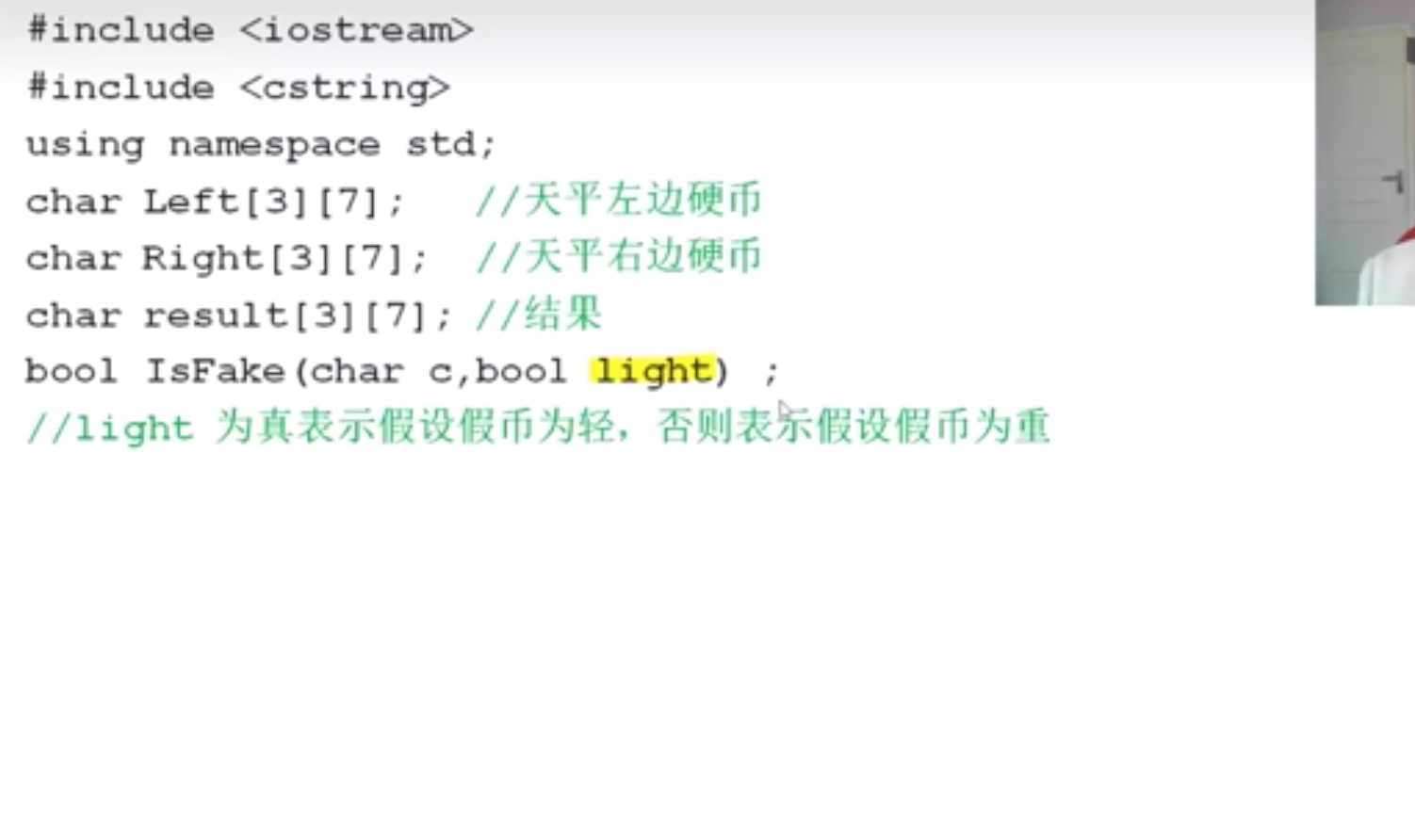
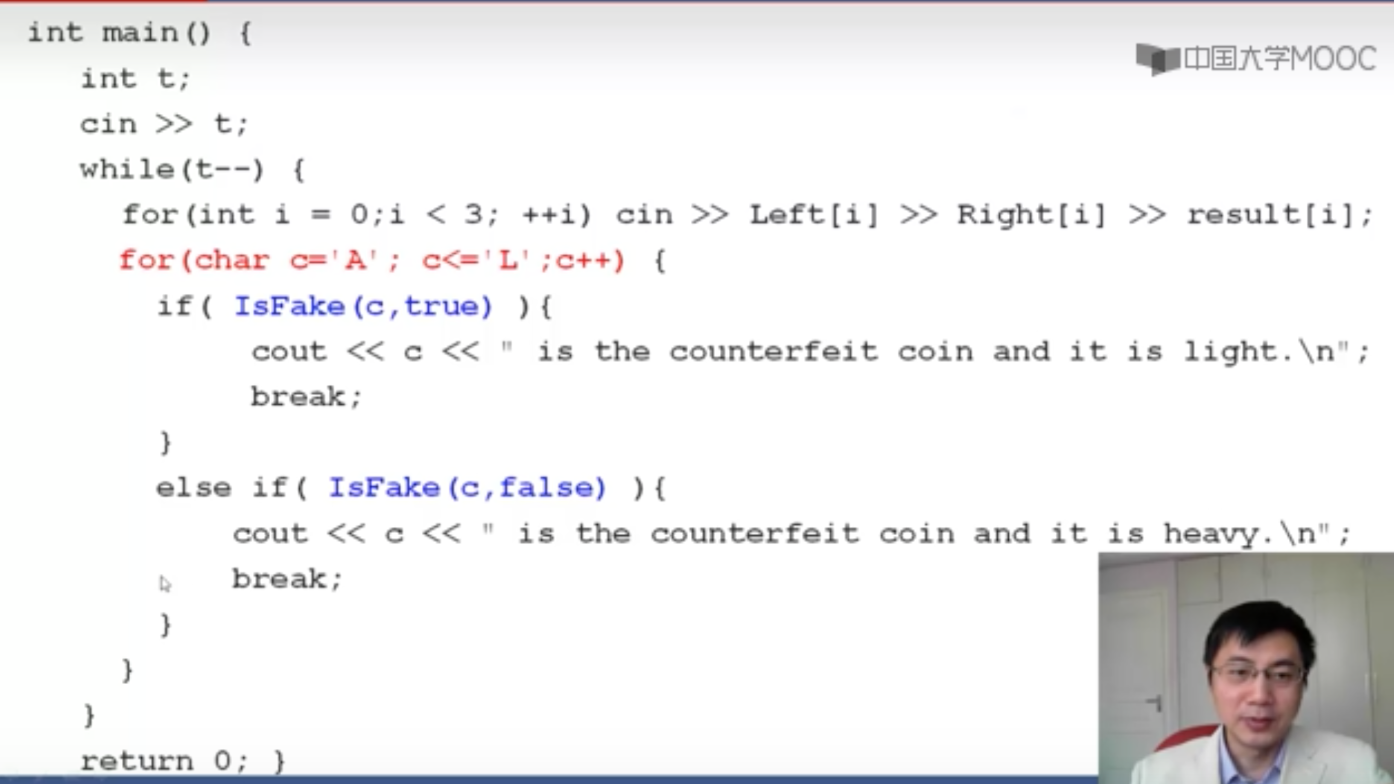

如果假币轻,则应该出现在高的那一边,重,则出现在低的那一边,且天平平衡时肯定没有出现假币,每次枚举时都进行判断,如果结果正确则说明假设正确,这枚币为假币并且轻重也是假设正确
4、熄灯问题


输出的是开关按动的方案,并且注意一个开关按一次是开,按两次就是关相当于没按,所以开关值为0和1,不存在其他次数
而且开关次序也没关系,先按哪个再按哪个结果是一样的

一个简单的想法就是枚举所有开关的可能取值,即每个开关两个值0和1,状态数即2的30次方,超时,需要一种优化的方案

不对全部开关进行枚举,而是选择一部分,例如第一行的状态2的6次方确定后,想要改变第一行的状态只能改变第二行,第二行也就确定了,以此类推,那么后面也就确定,所以只需要遍历第一行的灯

优化算法:
输入存储:只需要一个一维的char类型数据,一个char为8位,一行只需要6位即可,一行6个比特,即5行5个char,使用位运算来进行
用二进制数进行枚举:对于第一行的枚举可以优化为,对于2的次方的枚举,可以用int来累加从0开始到2的k次方减1,即k位01的组合,即2的k次方减1种,例如00,01,10,11->0,1,2,3,用二进制数进行枚举


Tips:
开数组时为了具有一定的容错率,需要设置数组大小比实际所需的大小要多,以防止程序逻辑缺陷导致的数组越界使得程序崩溃。
最后
以上就是精明钻石最近收集整理的关于程序设计与算法基础---枚举的全部内容,更多相关程序设计与算法基础---枚举内容请搜索靠谱客的其他文章。








发表评论 取消回复