| 二叉树 |
|
|---|
| 自平衡二叉查找树 |
|
|---|
| B树 |
|
|---|
| Trie |
|
|---|
| 空间划分树 |
|
|---|
| 非二叉树 |
|
|---|
| 其他类型 |
|
|---|
二叉树:
任何节点最多只允许有两个子节点。
二叉搜索树:
可以提供对数时间的元素插入和访问。任何节点的键值一定大于其左子树中的每一个节点的键值,并不小于其右子树中的每一个节点的键值。
平衡二叉搜索树:
平衡的意思是,没有任何一个节点过深(深度过大)。二叉搜索树可能会在多次插入或删除之后,变得不平衡。
AVL-tree是一个"加上了额外平衡条件"的二叉搜索树,其平衡条件的建立是为了确保整棵树的深度为O(logN)。要求任何节点的左右子树高度相差最多1。
根节点到任一节点的路径长度,即所谓该节点的深度。根节点的深度永远为0.
平衡树和不平衡树的区别: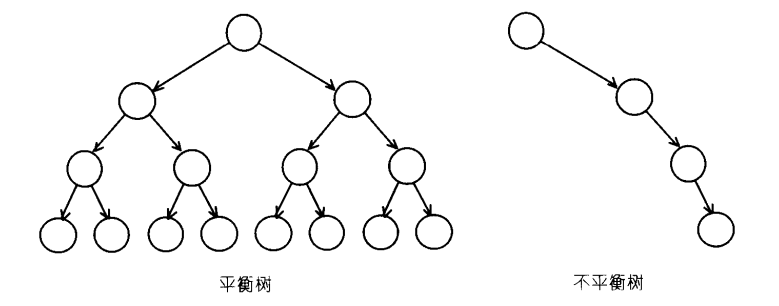
插入节点11之后,树变得不平衡了:
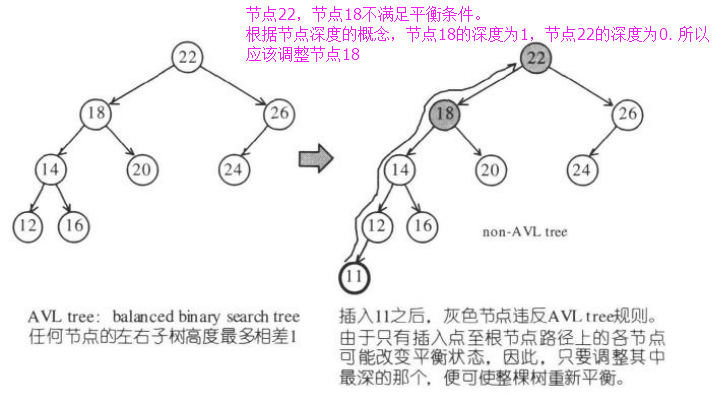
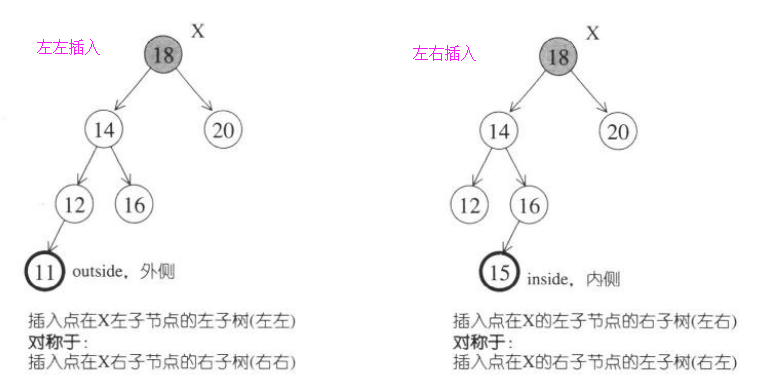
插入节点破坏了平衡条件的四种情况:

情况1,4对称,称为外侧插入,可以采用单旋转操作调整解决。
情况2,3对称,称为内侧插入,可以采用双旋转操作调整解决。
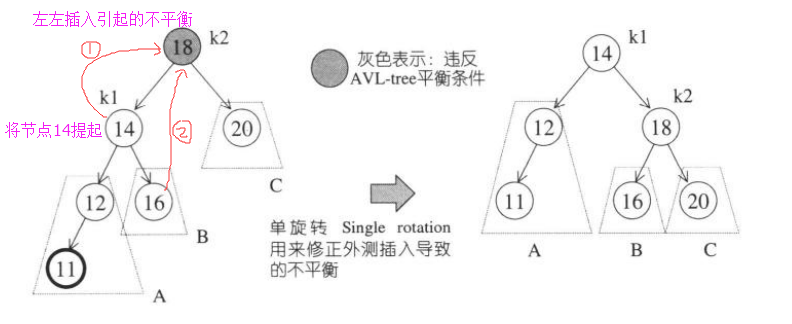
单旋转(旋转的情况为外侧插入):
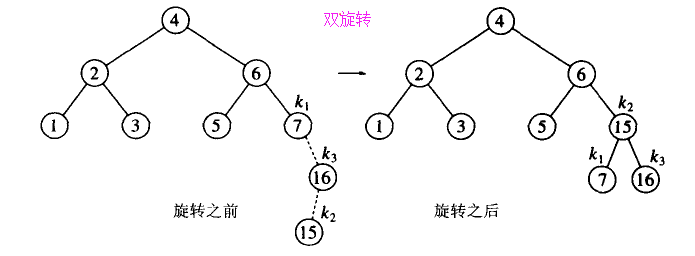
双旋转(旋转的情况为内侧插入):
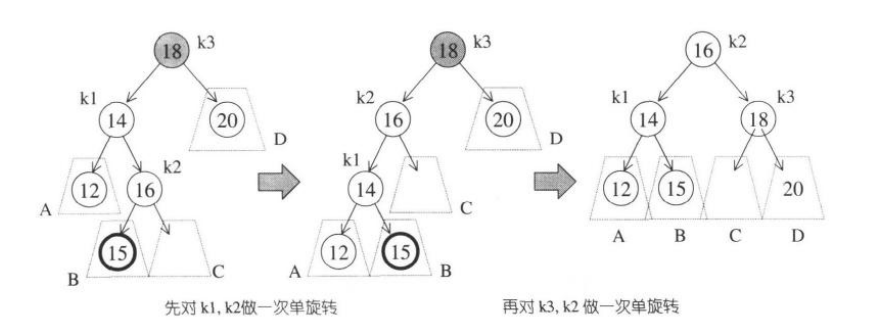
对于双旋转的情况,有一个特殊之处,比如上图,因为插入了15,引起了18的不平衡。15肯定是介于18和18的左子树之间的值。此时肯定要双旋转。
如果15的父节点不是18的子节点(上面的情况)双旋转其实就是将15的父节点代替18结点。(当然还是要旋转的,这只是一个特点)
如果15的父节点16是7的子节点(下面的情况)双旋转其实就是将15节点代替7结点。(当然还是要旋转的,这只是一个特点)
最后
以上就是失眠月饼最近收集整理的关于数据结构与算法——AVL树简介的全部内容,更多相关数据结构与算法——AVL树简介内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复