Day26 容斥原理 nim游戏 异或高斯消元 台阶nim游戏 拆分nim游戏

容斥原理

就是计算n个有交集集合的总面积大小的规律

传送门

所有项的数量是C(n,1)+C(n,2)+……+C(n,n)=2ⁿ
位数是m
所以复杂度是O(m*2^m)
此题刚好是2⁴*2¹⁶=2²⁰=10⁶
1e6的复杂度
运用状态压缩把所有可能的集合都罗列出来
用位运算判断1的个数是否为偶数，为奇数就加起来，否则减掉
并且把集合要除掉的数不断相乘，直至其大于n
因为大于n的话，1~n里就没有这个数的倍数了，所以不必加上这个答案

#include<iostream>
using namespace std;
typedef long long LL;
const int N=20;
int p[N];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<m;i++)cin>>p[i];
    
    int res=0;
    for(int i=1;i<1<<m;i++){
        int cnt=0,t=1;
        for(int j=0;j<m;j++){
            if(i>>j&1){
                if((LL)t*p[j]>n){
                    t=-1;
                    break;
                }
                cnt++;
                t*=p[j];
            }
        }
        
        if(t!=-1){
            if(cnt%2){
                res+=n/t;
            }else {
                res-=n/t;
            }
        }
    }
    cout<<res;
    return 0;
}

nim游戏

就是有很多堆石子
你和队手每步可以取任意一堆石子的任意数量，至少取一个
没法行动的那一方就输

结论是
如果每一堆石子数量异或起来是0先手必败，否则必胜
传送门

#include<iostream>
using namespace std;

int main(){
    int n;
    cin>>n;
    int res=0;
    for(int i=0;i<n;i++){
        int t;
        cin>>t;
        res^=t;
    }
    if(!res)puts("No");
    else puts("Yes");
    return 0;
}

nim游戏基础上
给出m个数，让你只能取其中数的个数石子
问先手是否必胜

这就涉及到sg函数
我们设必败态的sg函数为0
mex({})返回的是集合中不存在并且最小的非0的数
比如{0,1,3}就返回2

那么就可以画出每一堆石子的决策图

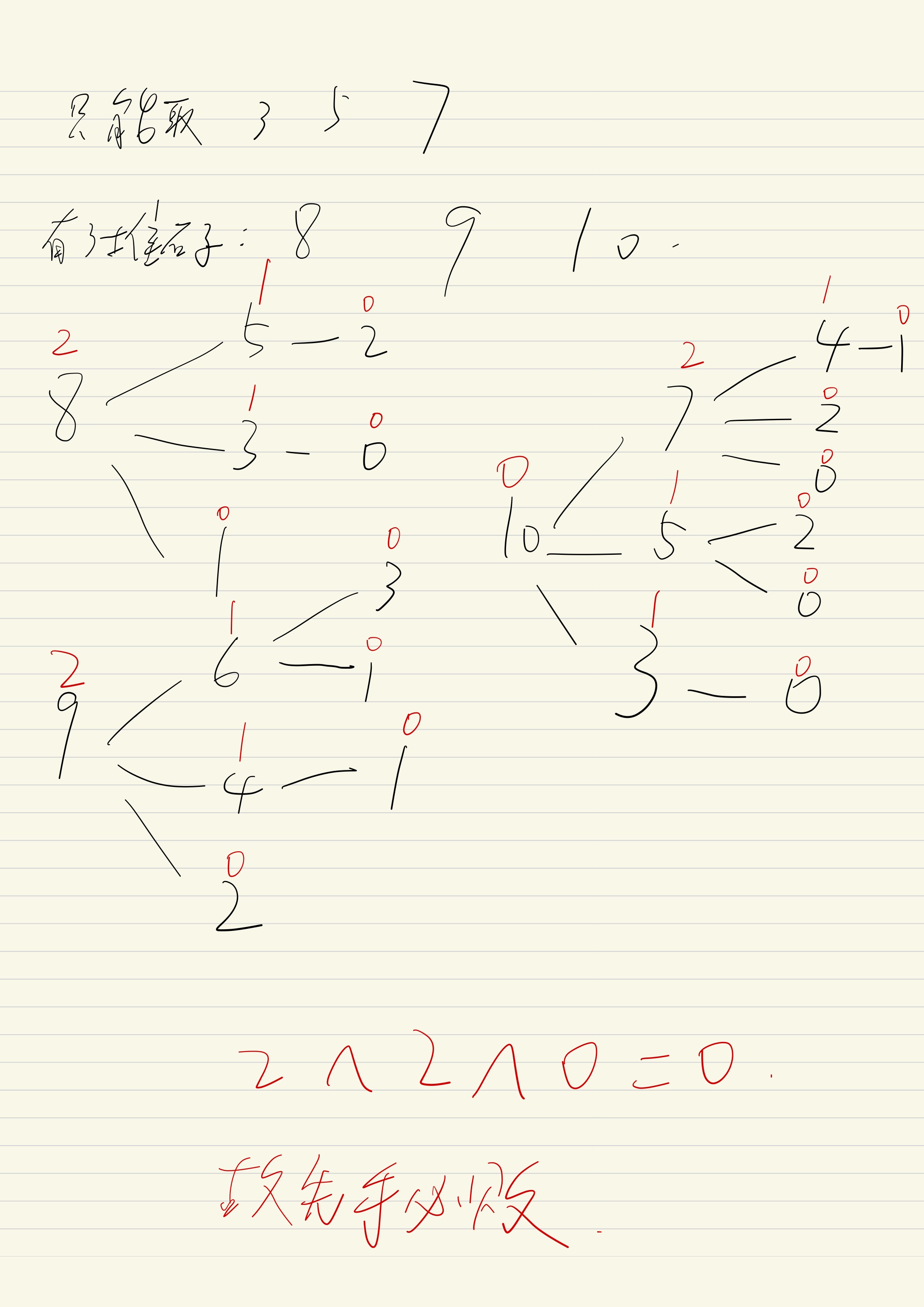
传送门

#include<iostream>
#include<cstring>
#include<unordered_set>
using namespace std;
const int N=110,M=10010;
int s[N],f[M];
int n,m;

int sg(int x){
    
    if(f[x]!=-1)return f[x];
    
    unordered_set<int>S;
    for(int i=0;i<m;i++){
        int sum=s[i];
        if(x-sum>=0)S.insert(sg(x-sum));
    }
    
    for(int i=0;;i++)
        if(!S.count(i))
            return f[x]=i;
}

int main(){
    cin>>m;
    for(int i=0;i<m;i++)cin>>s[i];
    cin>>n;
    int res=0;
    memset(f,-1,sizeof f);
    for(int i=0;i<n;i++){
        int t;
        cin>>t;
        res^=sg(t);
    }
    if(!res)puts("No");
    else puts("Yes");
    return 0;
}

异或高斯消元

其实和加法一样
把方程消成上三角就可以
传送门

#include<iostream>
using namespace std;
const int N=110;
int n,op[N][N];

int guass(){
    int r,c;
    for(r=0,c=0;c<n;c++){
        int t=r;
        for(int i=r;i<n;i++){
            if(op[i][c]){
                t=i;
                break;
            }
        }
        
        //记得在没有1的时候跳掉
        if(!op[t][c])continue;
        //移到最上面,交换的时候要等于n
        for(int i=c;i<=n;i++)swap(op[t][i],op[r][i]);
        //消元
        for(int i=r+1;i<n;i++){
            if(op[i][c]){
                for(int j=c;j<=n;j++){
                    op[i][j]^=op[r][j];
                }
            }
        }
        r++;
    }
    
    if(r<n){
        for(int i=r;i<n;i++){
            if(op[i][n])return 2;
        }
        return 1;
    }
    
    for(int i=r-1;i>=0;i--){
        for(int j=i+1;j<n;j++){
            op[i][n]^=op[i][j]&op[j][n];
        }
    }
    return 0;
}


int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<n+1;j++){
            cin>>op[i][j];
        }
    }
    
    int t=guass();
    
    if(!t){
        for(int i=0;i<n;i++){
            cout<<op[i][n]<<endl;
        }
    }else if(t==1){
        puts("Multiple sets of solutions");
    }else {
        puts("No solution");
    }
    return 0;
}

台阶nim游戏

观察可得

偶数台阶的石子不需要管
所有奇数台阶上的石子构成普通nim游戏
传送门

#include<iostream>
using namespace std;

const int N=1e5+10;

int main(){
    int res=0;
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        int t;
        cin>>t;
        if(i&1){
            res^=t;
        }
    }
    if(res)puts("Yes");
    else puts("No");
    return 0;
}

拆分nim游戏

传送门

其实就是换一下sg函数的求法

因为一个堆可以生成2个小堆
而这个过程是有限的
所以通过递归
并且sg(x)=sg(i)^sg(j)
不是很懂这个原理

#include<unordered_set>
#include<cstring>
#include<iostream>
using namespace std;
const int N=110;
int op[N],f[N];

int sg(int x){
    if(f[x]!=-1)return f[x];
    unordered_set<int>S;
    for(int i=0;i<x;i++){
        for(int j=0;j<=i;j++){
            S.insert(sg(i)^sg(j));
        }
    }
    
    for(int i=0;;i++)
        if(!S.count(i))
            return f[x]=i;
}

int main(){
    int n;
    cin>>n;
    memset(f,-1,sizeof f);
    int res=0;
    for(int i=0;i<n;i++){
        cin>>op[i];
        res^=sg(op[i]);
    }
    
    if(res)puts("Yes");
    else puts("No");
    return 0;
}

最后

以上就是落后墨镜为你收集整理的Day26 容斥原理 nim游戏 异或高斯消元 台阶nim游戏 拆分nim游戏的全部内容，希望文章能够帮你解决Day26 容斥原理 nim游戏 异或高斯消元 台阶nim游戏 拆分nim游戏所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。