1. 首页
  2. 文章中心
  3. 山东大学

山东大学众智课程——网络（图）有关的实验

57 阅读 0 评论
我是靠谱客的博主 拉长向日葵，最近开发中收集的这篇文章主要介绍山东大学众智课程——网络（图）有关的实验，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1.概述

本门课的核心是网络的概念——网络是事物之间相互关联的一种模式。比如我们身在其中的社会网络，体现朋友之间的社交联系。等等。

1.1网络的基本问题

先放几个社会中的网络结构

金融机构之间的借贷网络，其展现与标注方式揭示了不同部分及其作用。

金融

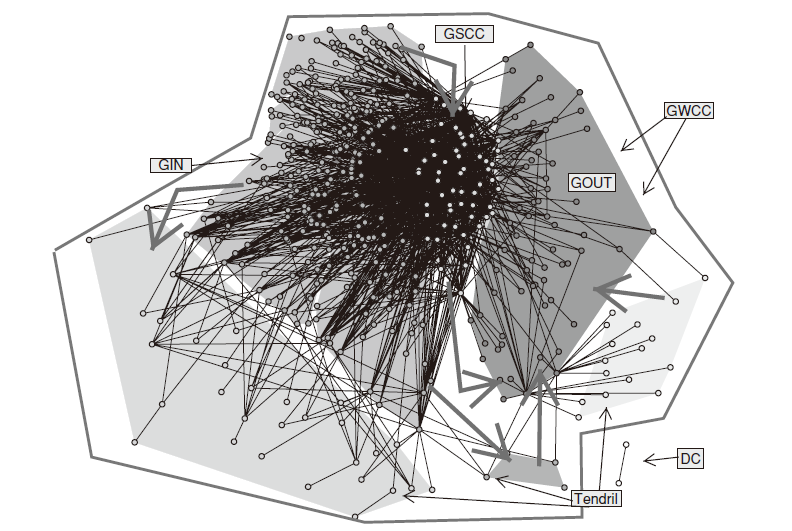
2004年美国总统大选前政治性博客的网络结构

在这里插入图片描述

行为及其动力学

当人们谈及复杂系统的连通性时，实际上是在讨论两个相关问题——结构层面的连通性（谁和谁相连）；另一个是在行为层面的连通性（每个个体的行动对于系统中每个其他个体都有隐含的后果。）
在Google上对Youtube的查询量随时间的变化情况
在这里插入图片描述
这种增长的可见性是整个人群行为的聚集效果。要理解这些过程是如何工作的，他们是怎么通过许多人互相关联的行为实现的，需要研究聚合行为的动力学。

多学科思想的交织

会用到数学建模的思想，建模是一个很重要的思想，是将实际问题转换为数学问题的过程。“不能用数学语言描述的知识不能够称为科学，不能被建模的实际问题不能算是实际解决了。”（来自某某某的吹牛），反正很重要就对了。
本书的中心目标之一，就是要将各领域分别的研究实践结合起来，以帮助形成这样一个综合。

1.2本书的核心内容

两个主要理论图论和博弈论。
图论不用说了，没学过图论的人都不能称作学过计算机。
博弈论是本书的特色——博弈论提供了关于个体行为的一种模型，要点在于个体行为的结果取决于其他个体的行为。

2.实验

2.1计算聚集系数和邻里重叠度

要求

输入：任意图的邻接矩阵
输出：
1）每个节点的聚集系数
2）每个节点对的邻里重叠度

相关定义

1）三元闭包：在一个社交圈内，若两个人有一个共同的朋友，则这两个人在未来成为朋友的可能性就会提高。
2）聚集系数：节点A的聚集系数定义为A的任意两个朋友彼此也是朋友的概率——也就是A相邻的节点之间边的实际数/与A相邻节点对的个数之比
下图中A的聚集系数a)是1/6 b)是1/2
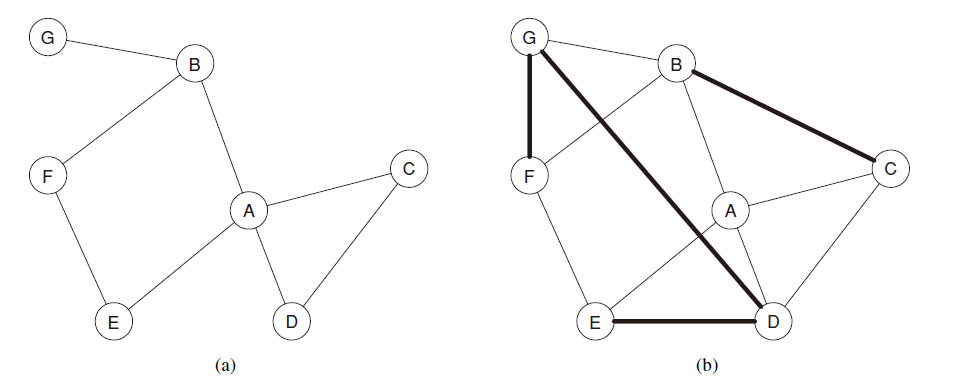
在这里插入图片描述
3）桥(Bridge)与捷径(Local bridge)：桥是指两个端点之间唯一的路径如下图A与B之间的边就是桥。
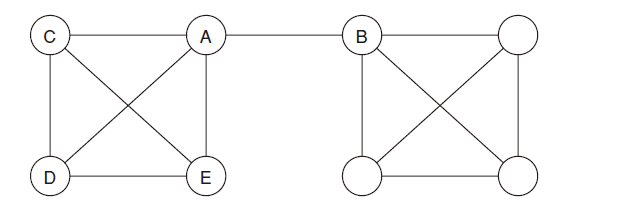
在这里插入图片描述
捷径：如果边AB的端点A和B没有共同的朋友，则称边AB为捷径。如下图
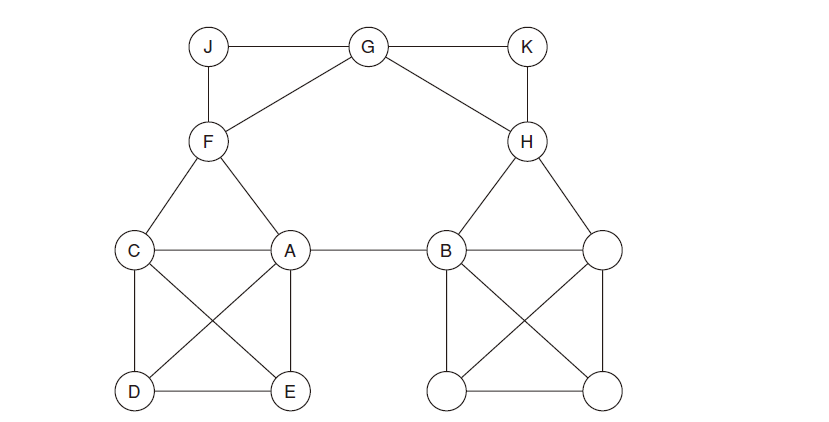
在这里插入图片描述
关系:从图中可以明显的看出,桥一定是捷径但是捷径不一定是桥.
4)强三元闭包性质:将社交网络中的所有关系分为两类-强联系(朋友)和弱联系(熟人),若节点A与节点B与C之间的关系均为强联系,且B和C之间无任何连接(强或弱),则称节点A违反了强三元闭包性质．否则，称节点A满足强三元闭包性质.
下图中所有的点都满足强三元闭包性质.
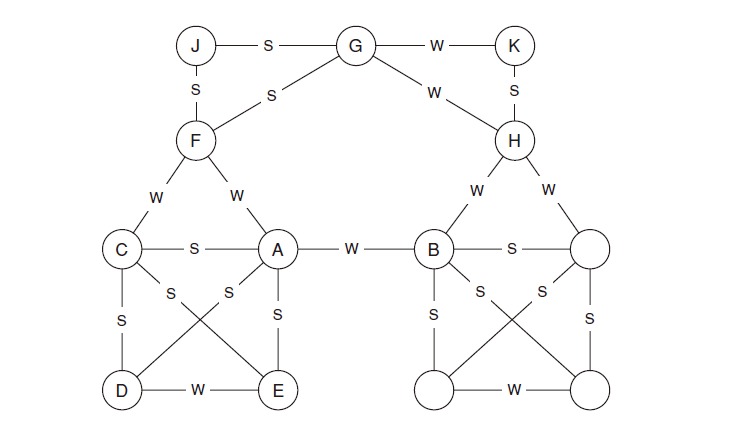
在这里插入图片描述
5)捷径与弱联系:在社交网络中,若节点A满足强三元闭包性质，并且至少有两个强联系边与之相连，则与其相连的任何捷径均为弱联系．
证明如下：
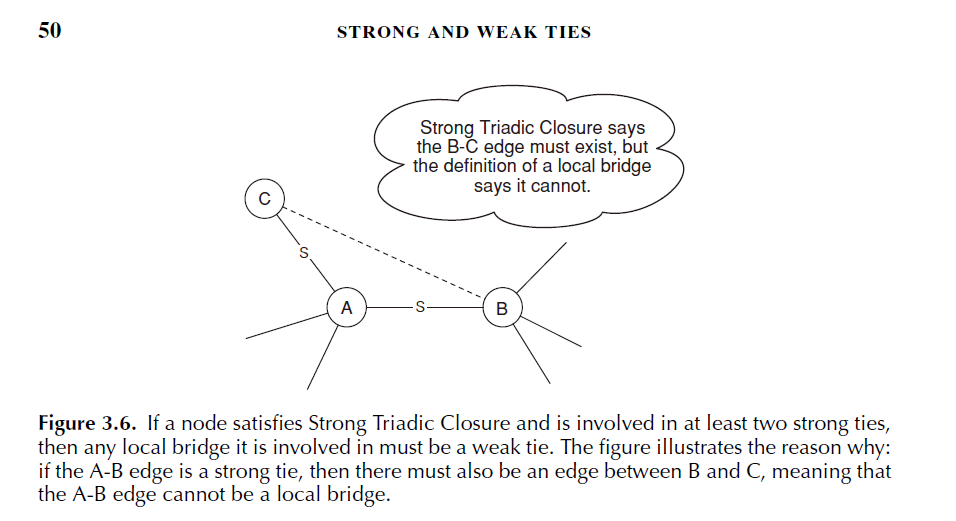
在这里插入图片描述
6)邻里重叠度:定义一条边的邻里重叠度为:与A,B均为邻居的节点数/与A,B中至少一个为邻居的节点数(不包含A，B)
可以看出当分子为零，即邻里重叠度为零时，该边是捷径．

算法及代码

算法：1）求聚集系数：先计算所有与当前节点连接的节点中间可能构成的连接（求法：（度（度-1）/2）（利用等差数列） 有多少个，这个数会作为分母，然后计算实际上有多少个节点被连接上了，这个数会作为分子。2）求邻里重叠度：定义(A, B)边的“与A、B均为邻居的节点数”与“与A、B中至少一个为邻居的节点数”的比值
输入如下图：

图结构(使用邻接矩阵储存图结构，主要的三个类的UML类图如下)：

主要代码：
graph

template <class T>
class graph{
public:
  virtual ~graph(){};

  virtual int numberOfVertices() const = 0;
  virtual int numberOfEdges() const = 0;
  virtual bool existsEdge(int ,int ) const = 0;
  virtual void insertEdge(edge<T>* ) = 0;//edge是一个模板类

  virtual void easeEdge(int ,int ) = 0;
  virtual int degree(int) const = 0;
  virtual int inDegree(int ) const = 0;
  virtual int outDegree(int ) const = 0;

  virtual bool directed() const = 0;
  virtual bool weighted() const = 0;

  //访问指定顶点的相邻顶点s
  virtual vertexIterator<T>* iterators(int ) = 0;

};

adjacencyWDigraph

template <class T>
class adjacencyWDigraph : public graph<T>{
protected:

  int n;
  int e;


  T noEdge;//表示不存在的边

public:

  T **a;//邻接矩阵

  //1.带有默认参数的构造器
  adjacencyWDigraph(int nV = 0,T theNoEdge =0){
      if(nV < 0){
          throw "顶点个数必须大于0!";
      }

      n = nV;
      e = 0;
      noEdge = theNoEdge;
      //make2dArray(a,n+1,n+1);
      //创建邻接矩阵

      a = new T*[n+1];//数组的数组是二维数组

      for (int j = 1; j <=n  ; ++j) {
          a[j] = new T[n+1];
      }

      for (int i = 1; i <= n ; ++i) {
          //初始化邻接矩阵
          for (int j = 1; j <=n ; ++j) {
              a[i][j] = noEdge;
          }
      }

  }




  int numberOfVertices() const { return n;}
  int numberOfEdges() const { return e;}
  bool directed() const { return true;}
  bool weighted() const { return true;}

  //2.判断（i，j）边是否存在
  bool existsEdge(int i,int j) const{
      if (i<1||j<1||i>n||j>n||a[i][j] == noEdge){
          return false;
      } else{
          return true;
      }
  }

  //3.插入边
  void insertEdge(edge<T>* theEdge){

      int v1 = theEdge->vertex1();
      int v2 = theEdge->vertex2();

      if(v1<1||v2<1||v1>n||v2>n||v1==v2){
          throw "如此插入非法！";
      } else{
          if (a[v1][v2] == noEdge){
              e++;
          }
          a[v1][v2] = theEdge->weight();
      }

  }

  //4.删除边
  void easeEdge(int i,int j){
      if(existsEdge(i,j)){
          a[i][j] = noEdge;
          e--;
      }
  }

  //5.顶点的度
  int degree(int theV) const{
      throw "有向图有入度和出度之分！";
  }

  //6.入度和出度
  int outDegree(int theV) const {

      int sum = 0;
      for (int i = 1; i <= n; ++i) {
          if (a[theV][i] != noEdge){
              sum++;
          }
      }

      return sum ;
  }
  int inDegree(int theV) const{
      int sum = 0;

      for (int i = 1; i <= n ; ++i) {
          if(a[i][theV] != noEdge){
              sum++;
          }
      }
      return sum;
  }

  //7.遍历器class
  class myIterator : public vertexIterator<T>{
  public:
      myIterator(T* theRow,T theNoEdge,int numberOfV){
          row = theRow;
          noEdge = theNoEdge;
          n = numberOfV;
          currentVertex = 1;
      }

      ~myIterator(){}

      int next(T & theWeight){
          for (int i = currentVertex; i <= n ; ++i) {
              if (row[i] != noEdge){
                  currentVertex = i+1;
                  theWeight = row[i];
                  return i;
              }
          }

          //不存在下一个邻接的顶点
          currentVertex = n+1;
          return 0;

      }

      int next(){
          for (int i = currentVertex; i <= n ; ++i) {
              if (row[i] != noEdge){
                  currentVertex = i+1;
                  return i;
              }
          }
          //不存在下一个邻接的顶点
          currentVertex = n+1;
          return 0;

      }

  protected:
      T* row;
      T noEdge;
      int n;
      int currentVertex;
  };

  myIterator* iterators(int theV){
      return new myIterator(a[theV],noEdge,n);
  }



};

adjacencyWGraph

template<class T>
class adjacencyWGraph : public adjacencyWDigraph<T> {
public:
  adjacencyWGraph(int numberOfVertices = 0, T theNoEdge = 0)
          : adjacencyWDigraph<T>(numberOfVertices, theNoEdge) {}

  void insertEdge(int v1, int v2, int weight) {
      if (v1 < 1 || v2 < 1 || v1 > this->n || v2 > this->n || v1 == v2) {
          throw "插入非法！";
      }

      //如果边不存在则插入
      if (this->a[v1][v2] == this->noEdge)
          this->e++;

      this->a[v1][v2] = weight;
      this->a[v2][v1] = weight;
  }

  bool directed() const { return false; }

  void eraseEdge(int i, int j) {
      if (i >= 1 && j >= 1 && i <= this->n && j <= this->n && this->a[i][j] != this->noEdge) {
          this->a[i][j] = this->noEdge;
          this->a[j][i] = this->noEdge;
          this->e--;
      }
  }

  int degree(int theVertex) const {
      int sum = 0;
      for (int j = 1; j <= this->n; j++)
          if (this->a[theVertex][j] != this->noEdge)
              sum++;

      return sum;
  }

  int outDegree(int theVertex) const {
      return degree(theVertex);
  }

  int inDegree(int theVertex) const {
      return degree(theVertex);
  }


//返回A的任意两个朋友之间也是朋友数目
  int getFriendsIsFriends(int iE) {

      int *friends = new int[degree(iE)];
      int start = 0;
      for (int j = 1; j <= this->n; ++j) {
          if (this->existsEdge(iE, j)) {
              friends[start++] = j;
//cout<<"邻接的顶点是："<<j<<endl;
          }
      }

      int friendsIsFriends = 0;
      //检查朋友之间是否为朋友
      for (int i = 0; i < degree(iE); i++) {
          //检查这一行的值
          for (int k = 0; k < degree(iE) - 1 - i; k++) {

              int a = friends[i];
              int b = friends[i + 1 + k];
              if (this->existsEdge(a, b)) {
                  friendsIsFriends++;
              }
          }
      }
      return friendsIsFriends;

  }

//返回与顶点i邻接的顶点
  int *getEdges(int i) {
      int *my_result = new int[this->degree(i)];
//cout<<i<<"度为："<<this->degree(i)<<endl;
      int start = 0;
      for (int j = 1; j <= this->n ; ++j) {
          if (this->existsEdge(i,j)){
              my_result[start++] = j;
//                cout<<i<<"的临界点有"<<j<<endl;
          }
      }
//cout<<i<<"的相邻的定点有几个："<< sizeof(my_result) <<endl;//返回的是指针的大小
      return my_result;
  }
};

求聚集系数

string aggCoeff[n+1];//记录每个顶点的聚集系数
    for (int k = 1; k <= n; ++k) {
        int my_degree = 0;

        my_degree = graph.degree(k);
//cout<<"度为"<<my_degree<<endl;cout<<endl;
        int denominator = my_degree*(my_degree-1)/2;
        if (denominator==0){
            aggCoeff[k]="0";
        } else{
            int molecule = graph.getFriendsIsFriends(k);
//cout<<"分子是："<<molecule<<endl;
            if(molecule==0){
                aggCoeff[k]="0";
            } else{
                int temp=molecule/denominator;
                if(temp==1){
                    aggCoeff[k]="1";
                } else{
                    aggCoeff[k]=to_string(molecule)+"/"+to_string(denominator);
                }
            }
        }
    }
    for (int l = 1; l <= n; ++l) {
        cout<<"顶点"<<l<<"的聚集系数为："<<aggCoeff[l]<<endl;
    }

求邻里间的聚集系数

//记录每对相邻节点的邻里重叠度
    string *degreeEdges = new string[e];
    int start2 = 0;
    for (int m = 1; m < n ; ++m) {
        for (int i = m+1; i <=n ; ++i) {
            if (graph.existsEdge(m,i)){
                //获得与A，B邻接的顶点
                int *getAEdges = graph.getEdges(m);
                int *getBEdges = graph.getEdges(i);

                int legA = graph.degree(m);
                int legB = graph.degree(i);

                if(legA==1&&legB==1){
                    degreeEdges[start2++]="0";
                } else{
                    int denominator = getDeno(getAEdges,getBEdges,legA,legB);
                    int molecule = getCoin(getAEdges,getBEdges,legA,legB);

                    if(denominator==molecule){
                        degreeEdges[start2++]="1";
                    } else if(molecule==0){
                        degreeEdges[start2++]="0";
                    } else{
                        degreeEdges[start2++]=to_string(molecule)+"/"+to_string(denominator);
                    }
                }

                cout<<"边（"<<m<<","<<i<<"）之间的邻里重叠度为："<<degreeEdges[start2-1]<<endl;

            }
        }
    }

2.2谢林模型模拟

要求

输入：n*n的矩阵，随机布局的两种节点
输出：
1）调节参数后输出相应的结果
2）需要有界面显示

相关定义

1)同质现象：我们和自己的朋友往往会有相同的特点，即谚语中所说的“物以类聚，人以群分。”
2）选择与社会影响：选择——人们更具相似的特征选择朋友，是一种主观的行为。社会影响——人们会因为需要和朋友们保持一致而改变自己的行为，这是一种客观的影响。
3）社团：社会交往的焦点。
4）归属网络（Affiliation Networks）：表明个体对社团的归属关系。是一个二分图。

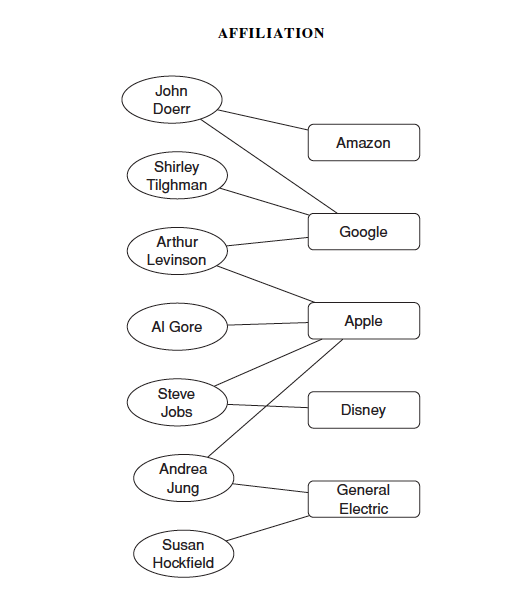
在这里插入图片描述

5）社会归属网络（social-affiliation network）：既包含一个个个体之间的社会网络又包含个体和社团之间的归属网络。

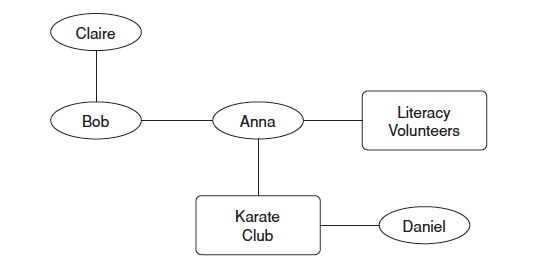
在这里插入图片描述

三元闭包原则在社会归属网络中有了新的拓展：

6）社团闭包（focal closure）：两个个体之间因为参加同一个社团而有建立连接的倾向。

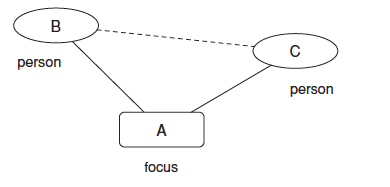
在这里插入图片描述

7）会员闭包（membership closure）：个体B会趋于参加朋友A参加的社团。

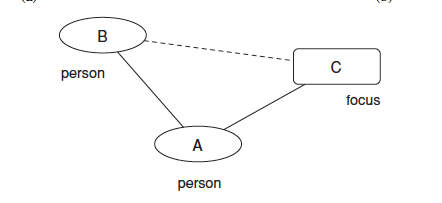
在这里插入图片描述

我们可以看出社团闭包是一种主观的选择而会员闭包是一种客观的社会影响。

8）谢林模型：描述的是同质性对于空间隔离的影响与作用。(像美国的唐人街和黑人聚集区都是谢林模型的表现。)

算法及代码

1）思想：
该模型的基本制约因素是，每一个代理要和一定量的同类代理成为邻居。 我们假设门槛值t适用于所有的代理：如果一个代理发现自己拥有比t少的邻居，他就有兴趣挪到其他的单元，我们称这样的代理不满意现状。 例如，图 (a)是对图(b)的一种标注，不满意现状的代理用“ * ”号指出，对应门槛值等于3中，我们在每个代理后也添加了一个号码，相当于给每个代理一个名字，不过这里的关键是区分代理是属千X类型还是O类型。

图（b）

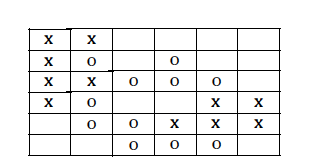
在这里插入图片描述

图（a）

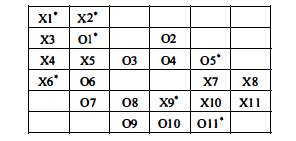
在这里插入图片描述

2）算法：逐步检测各个像素点是否低于门槛值，如果低于门槛值则搬家。

3）关键代码：

%根据百分比，计算像素点数量
empty_tmp = round(m * empty / 100); 
ratio_tmp = round((m - empty_tmp) * ratio / 100);
sim_tmp = sim / 100;
str_tmp = get(handles.round_text,'String'); %获取ROUND NUMBER的字符串
not_satis_red=[]; %初始化不满意红色点序列
not_satis_blue=[];%初始化不满意蓝色点序列
empty_now=[];%初始化空白像素点序列
%R(i,j)=1代表空置，2代表红点，3代表蓝点
for i=1:size
  for j=1:size
      switch R(i,j)
          case 1
              empty_now = [empty_now (j-1)*size+i];
          case 2
              satis_tmp = 0;
              amount_tmp = 0;
              %检测不满意情况    
              if i ~= 1 && R(i-1,j) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= 1 && R(i-1,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= size && R(i-1,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if j ~= 1 && R(i,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if j ~= size && R(i,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && j ~= 1 && R(i+1,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && R(i+1,j) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && j ~= size && R(i+1,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= 1 && R(i-1,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= 1 && R(i-1,j) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= 1 && j ~= size && R(i-1,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if j ~= 1 && R(i,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if j ~= size && R(i,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && j ~= 1 && R(i+1,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && R(i+1,j) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && j ~= size && R(i+1,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if satis_tmp<round(sim_tmp*amount_tmp)
                  not_satis_red =[not_satis_red (j-1)*size+i];
              end
          case 3
              satis_tmp = 0;
              amount_tmp = 0;
              if i ~= 1 && R(i-1,j) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= 1 && R(i-1,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= size && R(i-1,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if j ~= 1 && R(i,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if j ~= size && R(i,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && j ~= 1 && R(i+1,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && R(i+1,j) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && j ~= size && R(i+1,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= 1 && R(i-1,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= 1 && R(i-1,j) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= 1 && j ~= size && R(i-1,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if j ~= 1 && R(i,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if j ~= size && R(i,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && j ~= 1 && R(i+1,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && R(i+1,j) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && j ~= size && R(i+1,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if satis_tmp<round(sim_tmp*amount_tmp)
                  not_satis_blue =[not_satis_blue (j-1)*size+i];
              end
      end
  end
end

GitHub源代码

最后

以上就是拉长向日葵为你收集整理的山东大学众智课程——网络（图）有关的实验的全部内容，希望文章能够帮你解决山东大学众智课程——网络（图）有关的实验所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(38)

相关文章

子模集合函数（Submodular set function）
子模集合函数（Submodular set function）
众智科技上市：年营收2亿市值37亿 为杨新征及崔文峰家族企业
众智科技上市：年营收2亿市值37亿 为杨新征及崔文峰家族企业
mysql会员关系闭包表_Mysql闭包表之关于国家区域的一个实践
mysql会员关系闭包表_Mysql闭包表之关于国家区域的一个实践
超模函数与低模函数
超模函数与低模函数
山东大学众智课程——网络（图）有关的实验
山东大学众智课程——网络（图）有关的实验
对于三元闭包的感悟
对于三元闭包的感悟
山东大学软件学院众智科学与网络化产业（网络、群体与市场）复习笔记
山东大学软件学院众智科学与网络化产业（网络、群体与市场）复习笔记
博弈论题目总结（三）——组合游戏进阶
博弈论题目总结（三）——组合游戏进阶

评论列表共有 0 条评论

立即
投稿
返回
顶部