【众智实验三】山东大学软件学院众智实验三、探究极化关系下网络结构的稳定性（java）

实验目的：探究极化关系下网络结构的稳定性

实验步骤与内容：

输入：
任意极化关系下图的邻接矩阵（注意边有正负）
输出：
是否含有奇数个负向边的圈

步骤：

①编写代码从控制台获得输入。获得邻接矩阵mtr ; 在矩阵mtr中，1为正边，2为负边。

②识别以正边为基础的连通子图，numSection记录连通子图个数，通过BFS方法获得连通子图。

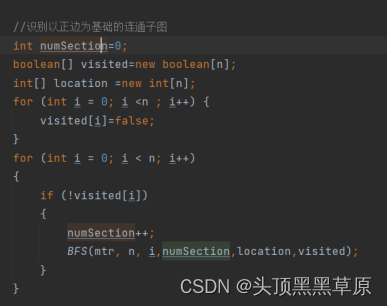
③进一步抽象将每个连通子图抽象为一个节点，获得新的邻接矩阵。新的邻接矩阵的大小为numsection^2,形成新矩阵的方法是遍历整个矩阵的负向边，构建各个连通子图之间的边。

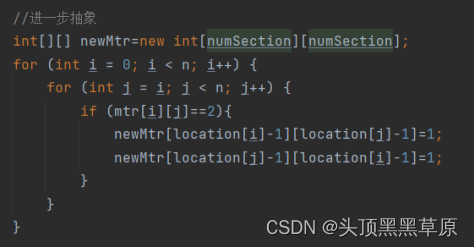
④BFS遍历新的邻接矩阵，并记录每个节点的层数，若不存在同层节点之间的边，则
不存在含奇数个负向边的圈，反之，则存在。

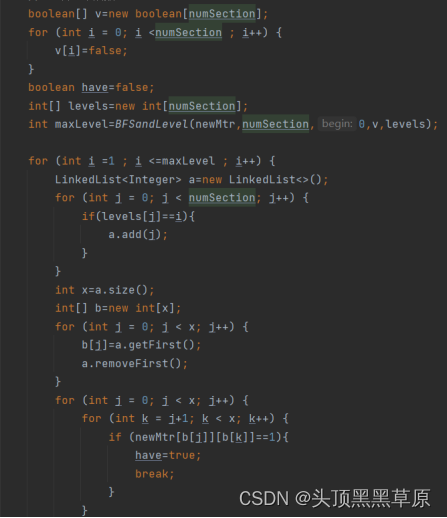
⑤输出结果

结果测试：

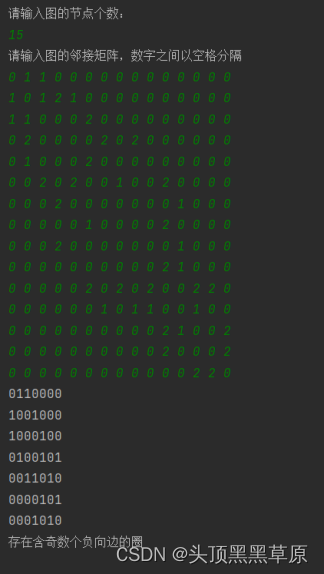
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class test03 {
public static void main(String[] args) {
//图的输入
Scanner sc=new Scanner(System.in);
System.out.println("请输入图的节点个数：");
int n=sc.nextInt();
String t=sc.nextLine();
String[] strs=new String[n];
int[][] mtr=new int[n][n];
System.out.println("请输入图的邻接矩阵，数字之间以空格分隔");
for(int i=0;i<n;i++){
strs[i]=sc.nextLine();
String[] ss=strs[i].split(" ");
int j=0;
for (String s:ss){
mtr[i][j]=Integer.parseInt(s);
j++;
}
}
//识别以正边为基础的连通子图
int numSection=0;
boolean[] visited=new boolean[n];
int[] location =new int[n];
for (int i = 0; i <n ; i++) {
visited[i]=false;
}
for (int i = 0; i < n; i++)
{
if (!visited[i])
{
numSection++;
BFS(mtr, n, i,numSection,location,visited);
}
}
//进一步抽象
int[][] newMtr=new int[numSection][numSection];
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
if (mtr[i][j]==2){
newMtr[location[i]-1][location[j]-1]=1;
newMtr[location[j]-1][location[i]-1]=1;
}
}
}
for (int i = 0; i <numSection ; i++) {
for (int j = 0; j < numSection; j++) {
System.out.print(newMtr[i][j]);
}
System.out.println();
}
//BFS并记录层数
boolean[] v=new boolean[numSection];
for (int i = 0; i <numSection ; i++) {
v[i]=false;
}
boolean have=false;
int[] levels=new int[numSection];
int maxLevel=BFSandLevel(newMtr,numSection,0,v,levels);
for (int i =1 ; i <=maxLevel ; i++) {
LinkedList<Integer> a=new LinkedList<>();
for (int j = 0; j < numSection; j++) {
if(levels[j]==i){
a.add(j);
}
}
int x=a.size();
int[] b=new int[x];
for (int j = 0; j < x; j++) {
b[j]=a.getFirst();
a.removeFirst();
}
for (int j = 0; j < x; j++) {
for (int k = j+1; k < x; k++) {
if (newMtr[b[j]][b[k]]==1){
have=true;
break;
}
}
}
}
//输出结果
if(have){
System.out.println("存在含奇数个负向边的圈");
}else{
System.out.println("不存在含奇数个负向边的圈");
}
}
public static void BFS(int[][] mtr,int n,int begin,int numSection,int[] location,boolean[] visited){
LinkedList<Integer> Q=new LinkedList<>();
Q.add(begin);
visited[begin]=true;
while (!Q.isEmpty()){
int tmp=Q.getFirst();
location[tmp]=numSection;
Q.removeFirst();
for (int i = 0; i < n; i++)
{
if (!visited[i] && mtr[tmp][i]==1)
{
Q.add(i);
visited[i] = true;
}
}
}
}
public static int BFSandLevel(int[][] mtr,int n,int begin,boolean[] visited,int[] levels){
LinkedList<Integer> Q=new LinkedList<>();
Q.add(begin);
visited[begin]=true;
int[] path=new int[n];
levels[begin]=1;
int level=1;
while (!Q.isEmpty()){
int tmp=Q.getFirst();
Q.removeFirst();
for (int i = 0; i < n; i++)
{
if (!visited[i] && mtr[tmp][i]==1)
{
Q.add(i);
visited[i] = true;
path[i]=tmp;
}
}
}
int maxLevel=level;
for (int i = 0; i < n; i++) {
if(i!=begin){
levels[i]=levels[path[i]]+1;
if (levels[i]>maxLevel){
maxLevel=levels[i];
}
}
}
return maxLevel;
}
}

最后

以上就是开放皮带为你收集整理的【众智实验三】山东大学软件学院众智实验三、探究极化关系下网络结构的稳定性（java）的全部内容，希望文章能够帮你解决【众智实验三】山东大学软件学院众智实验三、探究极化关系下网络结构的稳定性（java）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。