概述
一.组合数的计算方法
首先组合和排列数的定义在高中阶段已经知晓，这里主要探讨在算法竞赛中的应用。首先，我们通常把 C n m C_{n}^{m} Cnm写成 ( n m ) tbinom{n}{m} (mn)的形式（注意上下顺序是反过来的），初次看这种格式可能会不太适应。下面用一个例题配合多种数据范围介绍几种常用的组合数求法。
例题：给定 n 组询问，每组询问给定两个整数 a，b，请你输出 ( a b ) % P tbinom{a}{b} %P (ba)%P的值。
方法1
当数据范围比较小时，我们可以使用下面的递推公式去求答案
(
n
m
)
=
(
n
－１
m
)
+
(
n
－１
m
－１
)
tbinom{n}{m} = tbinom{n－１}{m} +tbinom{n－１}{m－１}
(mn)=(mn－１)+(m－１n－１)
关于这个高中我们就学过的式子，下面给一个较为直观的解释：
在a个苹果中,选出b个苹果出来,现有一个苹果p：
- 选这个苹果的方案相当于在剩余的a-1个苹果中选b-1个苹果
- 不选这个苹果的方案相当于在剩余的a-1个苹果中选b个苹果
将1,2两种方案相加就是在a个苹果中选择b个苹果。
code也很简洁
//假设数据范围a<=2000，模数P固定
void init()//预处理所有组合数出来
{
for(int i=0;i<=2000;i++)
{
for(int j=0;j<=i;j++)
{
if( !j ) c[i][j] = 1;
else c[i][j] = (c[i-1][j] + c[i-1][j-1] )%P;
}
}
}
int main()
{
cin>>n;
init();
while( n-- )
{
scanf("%lld %lld",&a,&b);
printf("%lldn",c[a][b]);
}
return 0;
}
方法2
当数据范围大一点的时候，方法一就不行了，我们需要从组合数的另一个公式入手：
(
n
m
)
=
n
!
(
n
−
m
)
!
×
m
!
tbinom{n}{m} = frac{n!}{(n-m)! times m! }
(mn)=(n−m)!×m!n!
但是我们注意题目一般都是要对一个数取模的，但是分母是不能直接取模的，所以我们要变成逆元的形式，不妨令
i
n
v
(
x
)
inv(x)
inv(x)表示
x
x
x在取模
P
P
P意义下的逆元
(
n
m
)
%
P
=
(
n
!
(
n
−
m
)
!
×
m
!
)
%
P
=
[
n
!
×
i
n
v
(
(
n
−
m
)
!
)
×
i
n
v
(
m
!
)
]
%
P
tbinom{n}{m}%P = (frac{n!}{(n-m)! times m! }) %P = [n! times inv( (n-m)! ) times inv( m! ) ]%P
(mn)%P=((n−m)!×m!n!)%P=[n! ×inv((n−m)!)×inv(m!)]%P
我们一般碰到的模数都是一个大质数，在这简单回忆用费马小定理求逆元（此方法极为重要，日后求逆元基本都是用这个）：
当P是质数时， i n v ( x ) = x P − 2 inv(x) = x^{P-2} inv(x)=xP−2，用快速幂即可
code：
const LL p = 1e9+7;//假设模数固定
LL quick_pow(LL a,LL b,LL p)//快速幂函数
{
LL ans = 1;
while( b )
{
if( b&1 ) ans = ans * a % p;
a = a*a % p;
b>>=1;
}
return ans;
}
LL n,fact[N],infact[N],a,b;//fact存阶乘，infact存阶乘的逆元
void init()
{
fact[0] = infact[0] = 1;
for(int i=1;i<N;i++)
{
fact[i] = ( fact[i-1] * i ) % p;
infact[i] = ( infact[i-1] * quick(i,p-2,p) ) % p;
}
}
int main()
{
scanf("%lld %lld",&a,&b);
printf("%lldn", fact[a] * infact[b] % MOD * infact[a-b] % MOD );
return 0;
}
方法3
当数据范围大到
1
0
18
10^{18}
1018这种不可能预处理阶乘的大小时，我们需要用到一个新的定理来求。这就是卢卡斯定理，这里只给出公式，具体证明可自行搜索，这里不证。
(
n
m
)
≡
(
n
%
P
m
%
P
)
×
(
n
p
m
p
)
(
m
o
d
P
)
tbinom{n}{m} equiv tbinom{n%P}{m%P} times tbinom{frac{n}{p}}{frac{m}{p}}quad(mod : P)
(mn)≡(m%Pn%P)×(pmpn)(modP)
code中有注释
//卢卡斯定理
#define LL long long
const LL p = 1e5+7;
LL quick(LL a,LL b,LL p)//依然是快速幂求逆元
{
LL res = 1;
while( b )
{
if( b&1 ) res = res * a % p;
a = a * a % p;
b>>=1;
}
return res;
}
LL C(LL a,LL b,LL p)//把数值拆的很小后，用组合数定义公式求数
{
if( b>a ) return 0;
LL ans = 1;
for(int i=1,j=a;i<=b;i++,j--)
{
ans = ans * j % p;
ans = ans * quick( i,p-2,p ) % p;
}
return ans;
}
LL lucas(LL a,LL b,LL p)//卢卡斯定理
{
if( a<p && b<p ) return C(a,b,p);
return C( a%p,b%p,p ) * lucas( a/p,b/p,p )%p;
}
int main()
{
LL n,a,b;
scanf("%lld %lld",&a,&b);
printf("%lldn",lucas(a,b,p));
return 0;
}
二.卡特兰数
有很多种方式可以推出卡特兰数的公式，这里选择较为通俗易懂的方式来讲述。（毕竟别的比如生成函数来推导太噩梦了 ）我们从几个经典的问题来了解一下卡特兰数。
经典问题1：进出栈序列
题目描述
n 个元素进栈序列为：1，2，3，4，…，n，则有多少种出栈序列。
（这是一道最经典的入门级卡特兰数题目，后面的例题跟这个差不多。）
分析：我们将进栈表示为 +1，出栈表示为 -1，则 1 3 2 的出栈序列可以表示为：+1 -1 +1 +1 -1 -1。过程如下图。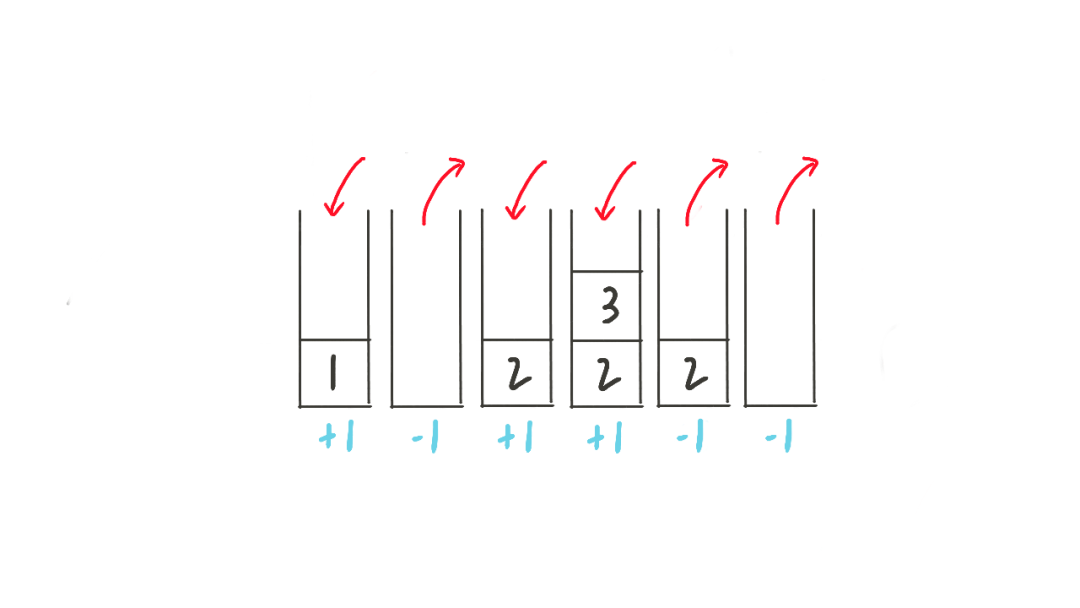
根据栈本身的特点，每次出栈的时候，必定之前有元素入栈，即对于每个 -1 前面都有一个 +1 相对应。因此，出栈序列的所有前缀和必然大于等于 0，并且 +1 的数量 等于 -1 的数量。
接下来让我们观察一下 n = 3 的一种出栈序列：+1 -1 -1 +1 -1 +1。序列前三项和小于 0，显然这是个非法的序列。
如果将 第一个 前缀和小于 0 的前缀，即前三项元素都进行取反，就会得到：-1 +1 +1 +1 -1 +1。此时有 3 + 1 个 +1 以及 3 - 1 个 -1。
因为这个小于 0 的前缀和必然是 -1，且 -1 比 +1 多一个，取反后，-1 比 +1 少一个，则 +1 变为 n + 1 个，且 -1 变为 n - 1 个。进一步推广，对于 n 元素的每种非法出栈序列，都会对应一个含有 n + 1 个 +1 以及 n - 1个 -1 的序列。
那么我们会有一个问题：如何证明这两种序列是一一对应的？
可以假设非法序列为 A，对应的序列为 B。每个 A 只有一个"第一个前缀和小于 0 的前缀"，所以每个 A 只能产生一个 B。而每个 B 想要还原到 A，就需要找到"第一个前缀和大于 0 的前缀"，显然 B 也只能产生一个 A。
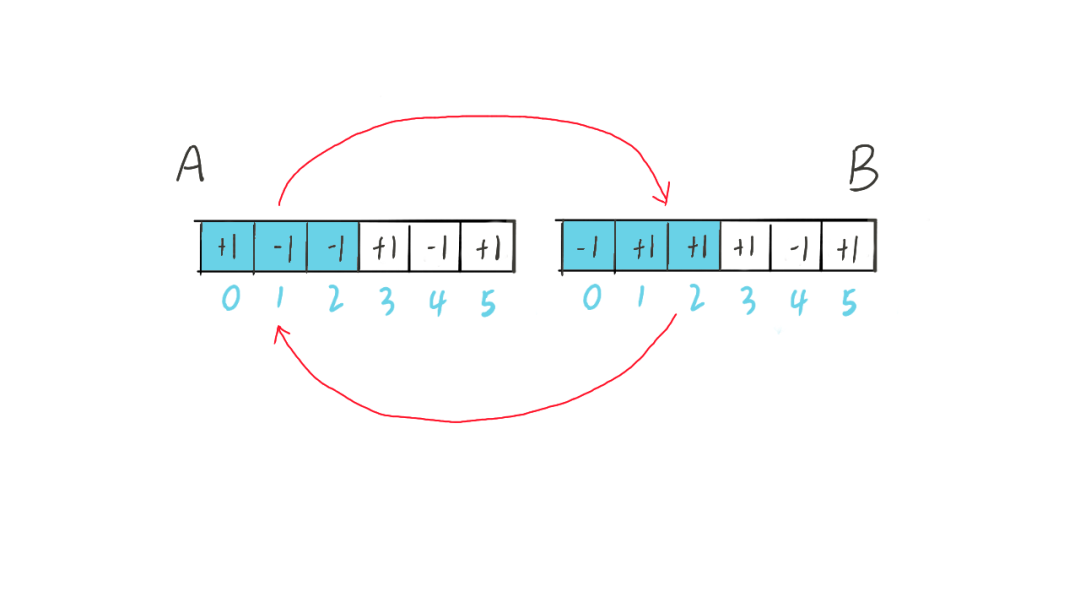
每个 B 都有 n + 1 个 +1 以及 n - 1 个 -1，因此 B 的数量为
(
2
n
n
+
1
)
tbinom{2n}{n+1}
(n+12n)，相当于在长度为 2n 的序列中找到n + 1个位置存放 +1。相应的，非法序列的数量也就等于
(
2
n
n
+
1
)
tbinom{2n}{n+1}
(n+12n)。出栈序列的总数量共有
(
2
n
n
)
tbinom{2n}{n}
(n2n)，因此，合法的出栈序列的数量为
(
2
n
n
)
−
(
2
n
n
+
1
)
tbinom{2n}{n} - tbinom{2n}{n+1}
(n2n)−(n+12n)。
到此为止，我们已经得到了卡特兰数的通项 ( 2 n n ) − ( 2 n n + 1 ) = ( 2 n n ) n + 1 tbinom{2n}{n} - tbinom{2n}{n+1} = frac{ tbinom{2n}{n} }{n+1} (n2n)−(n+12n)=n+1(n2n) 。
经典问题2：括号序列
题目描述
n 对括号，则有多少种 “括号匹配” 的括号序列
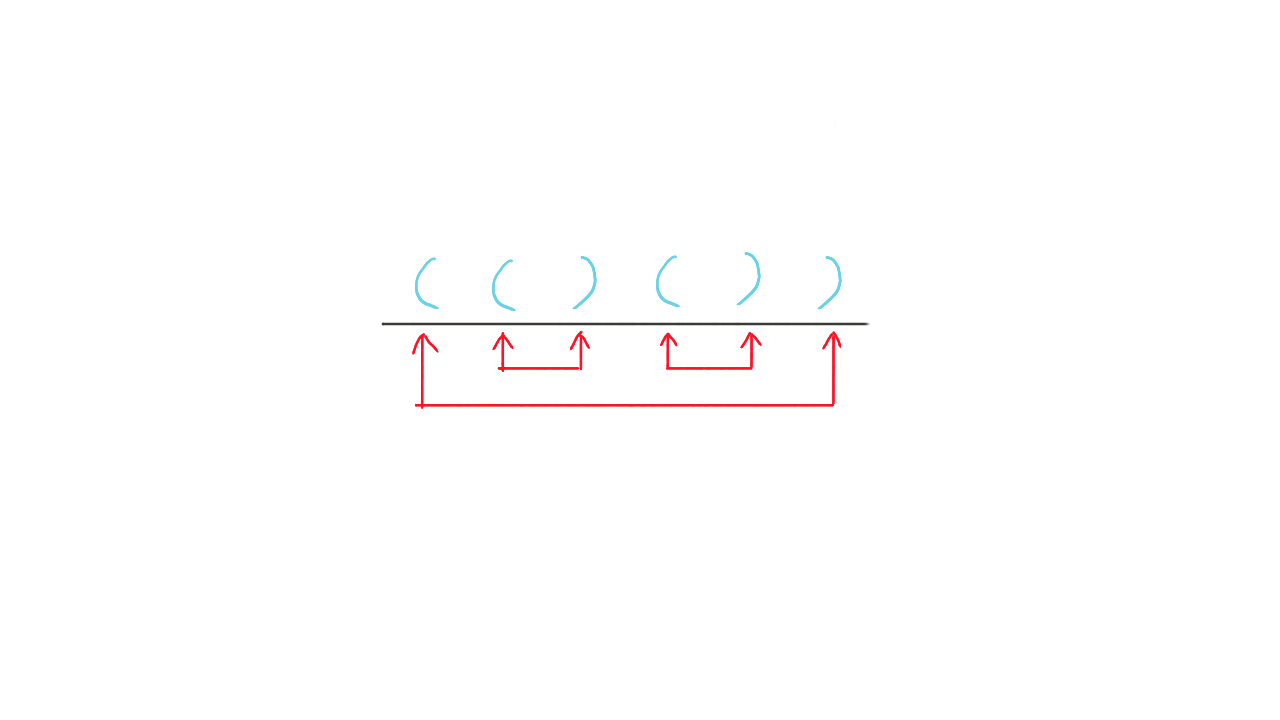
分析： 左括号看成 +1，右括号看成 -1，那么就和上题的进出栈一样，共有
(
2
n
n
)
−
(
2
n
n
+
1
)
=
(
2
n
n
)
n
+
1
tbinom{2n}{n} - tbinom{2n}{n+1} = frac{ tbinom{2n}{n} }{n+1}
(n2n)−(n+12n)=n+1(n2n) 种序列。
经典问题3：买票找零问题
题目描述
电影票一张 50元，且售票厅一开始没有零钱。m 个人各自持有 50元，n 个人各自持有 100元。则有多少种排队方式，可以让每个人都买到电影票。
分析：持有 50 元的人每次购票时不需要找零，并且可以帮助后面持有 100元的人找零；而对于持有 100元的人每次购票时需要找零，但100元对后面的找零没有任何作用。
因此，相当于每个持有 100元 的人都需要和一个持有 50元 的人进行匹配。我们将持有 50元的标记为 +1，持有 100元的标记为 -1，此时我们会惊喜地发现这个问题跟经典问题1也是差不多的！
但是但是，不同的是，这题 m 并一定等于 n，且排队序列是一种排列，需要考虑先后顺序，例如各自持有 50元 的两个人的前后关系互换会造成两种不同的排队序列。故在此我们乘上相应排列的数目，最后答案是 [ ( n + m m ) − ( n + m m + 1 ) ] × n ! × m ! [tbinom{n+m}{m} - tbinom{n+m}{m+1}] times n! times m! [(mn+m)−(m+1n+m)]×n!×m!种。
代码实现
上面我们已经推出了通式
C
n
=
(
2
n
n
)
−
(
2
n
n
+
1
)
=
(
2
n
n
)
n
+
1
C_n = tbinom{2n}{n} - tbinom{2n}{n+1} = frac{ tbinom{2n}{n} }{n+1}
Cn=(n2n)−(n+12n)=n+1(n2n)
根据公式配合组合数计算方法这可以直接求值了。除了这个通项公式之外，卡特兰数还有一个由该通项公式推导而来的递推公式更加常用：
C
n
+
1
=
4
n
+
2
n
+
2
C
n
C_{n+1} = frac{4n+2}{n+2} C_n
Cn+1=n+24n+2Cn
递推边界是
C
0
=
1
C_0=1
C0=1
一个例题
题意：就是经典问题1
code
int n;
long long f[25];//存储卡特兰数
void solve()
{
f[0] = 1;
cin >> n;
for (int i = 1; i <= n; i++) f[i] = f[i - 1] * (4 * i - 2) / (i + 1);
// 这里用的递推
cout << f[n] << endl;
return 0;
}
除了本文介绍的几种经典问题，还有很多问题最后也是可以推导到卡特兰数上的。感兴趣可以自行找资料。
最后
以上就是内向戒指为你收集整理的组合数求法、卡特兰数一.组合数的计算方法二.卡特兰数的全部内容，希望文章能够帮你解决组合数求法、卡特兰数一.组合数的计算方法二.卡特兰数所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复