《机器学习》+周志华+第五章习题+5.5实现标准BP算法和累积BP算法

43 阅读 0 评论 29 点赞

我是靠谱客的博主难过爆米花，最近开发中收集的这篇文章主要介绍《机器学习》+周志华+第五章习题+5.5实现标准BP算法和累积BP算法，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

5.5 试编程实现标准BP算法和累积BP算法，在西瓜数据集3.0上分别用这两个算法训练一个单隐层网络，并进行比较。

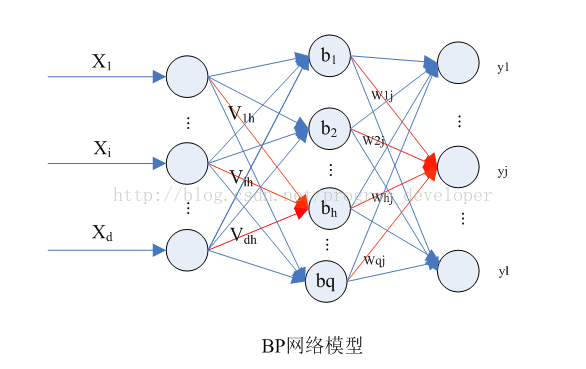
给定训练集D={(x1,y1),(x2,y2),......,(xm,ym)},其中输入示例由d个属性描述，输出l为实质向量。

图中拥有d个输入神经元、l个输出神经元、q个隐层神经元的多层前馈网络结构。

θj：表示输出层第j个神经元的阈值。

γh：表示隐层第h个神经元的阈值。

Vih：输入层第i个神经元与隐层第h个神经元直接的连接权值。

Whj：隐层第h个神经元与输出层第j个神经元之间的连接权值。

BP算法每次迭代都计算一个样本，最小化该样本输出值与真实值的差距，然后将修改过的参数传给下一个样本，直到达到收敛条件。这样做参数更新频繁，也可能出现参数更改相互抵消的情况，于是有了累积误差逆传播算法（ABP）。

ABP算法每次迭代都会先算出所有样本的输出，然后最小化整个样本输出与真实值的最小平方和，修改参数后进行下一次迭代。ABP参数更新次数比BP算法少的多，但是当累积误差降到一定程度时，进一步下降会非常缓慢。

迭代终止的条件：这里设置的终止条件是相邻一百次迭代的均方误差的差值不超过0.0001。

BP算法MATLAB语言：

clear

x = xlsread('E:machine_learningBPwatermelon3.0.xlsx', 'Sheet1', 'A1:Q8');
y = xlsread('E:machine_learningBPwatermelon3.0.xlsx', 'Sheet1', 'A9:Q9');
x=x';     %x进行转置 
y=y';     %y进行转置
%将y设置为0,1两类
y=y-1;
%获取输入参数的样本数与参数数
[m,d]=size(x);    %m是x矩阵的行数，表示总共有多少个训练集。d是矩阵的列数，表示训练集的输入。

OutputLayerNum=1;  %输出层神经元

v=rand(d,d+1);                      %输入层与隐层的权值,v是一个d行d+1列矩阵
w=rand(d+1,OutputLayerNum);         %隐层与输出层的权值,w是一个d+1行1列矩阵
gamma=rand(d+1);                    %隐层阈值,gamma是d+1行1列矩阵
theta=rand(OutputLayerNum);         %输出层阈值,theta是1行1列矩阵
py=zeros(m,OutputLayerNum);         %输出层输出
b=zeros(d+1);                       %隐层输出
g=zeros(OutputLayerNum);            %均方误差对w,gamma求导的参数
e=zeros(d+1);                       %均方误差对v,theta求导的参数

eta=1;                               %学习率


kn=0;        %迭代的次数
sn=0;        %同样的均方误差值累积次数
previous_E=0; %前一次迭代的累计误差
while(1)
    kn=kn+1;
    E=0;      %当前迭代的均方误差
    for i=1:m
      %计算隐层输出
      for j=1:d+1
        alpha=0;   %当前一个隐层节点神经元的输入
        for k=1:d
          alpha=alpha+v(k,j)*x(i,k);
         end
         b(j)=1/(1+exp(-alpha+gamma(j)));  %计算某个隐层节点的输出
       end
       %计算输出层输出
       for j=1:OutputLayerNum
         beta=0;
         for k=1:d+1
           beta=beta+w(k,j)*b(k);
         end
         py(i,j)=1/(1+exp(-beta+theta));
        end
        %计算当前一个训练数据的均方误差
        for j=1:OutputLayerNum
          E=E+((py(i,j)-y(i))^2)/2;
        end
        %计算w,beta导数参数
        for j=1:OutputLayerNum
          g(j)=py(i,j)*(1-py(i,j))*(y(i)-py(i,j));
        end
        %计算v,gamma导数参数
        for j=1:d+1
          teh=0;
          for k=1:OutputLayerNum
            teh=teh+w(j,k)*g(k);
          end
          e(j)=teh*b(j)*(1-b(j));
         end
         %更新v,gamma
         for j=1:d+1
           gamma(j)=gamma(j)+(-eta)*e(j);
           for k=1:d
             v(k,j)=v(k,j)+eta*e(j)*x(i,k);
            end
           end
          %更新w,theta
          for j=1:OutputLayerNum
            theta(j)=theta(j)+(-eta)*g(j);
            for k=1:d+1
              w(k,j)=w(k,j)+eta*g(j)*b(k);
             end
           end
         end
         %迭代终止判断
         if(abs(previous_E-E)<0.0001)
            sn=sn+1;
            if(sn==100)
               break;
             end
          else
             previous_E=E;
             sn=0;
         end
 end

西瓜3.0数据集在Excel中表示：

训练权重结果：

输出层输出结果： 真实结果：

这个实验的GitHub地址：https://github.com/Microstrong0305/Machine-Learning-ZhouZhiHua

ABP（accumulated error backpropagation）算法：即为累积BP算法，累积BP算法直接针对累积误差最小化，它在读取整个训练集D一遍后才对参数进行更新，其参数更新的频率低得很，但是在很多任务中，累积误差下降到一定程度之后，进一步下降会非常缓慢，这时标准BP往往会更快获得较好的解，尤其是在训练集D非常大时更新明显。

ABP算法的MATLAB实现:

clear

x = xlsread('E:machine_learningBPwatermelon3.0.xlsx', 'Sheet1', 'A1:Q8');
y = xlsread('E:machine_learningBPwatermelon3.0.xlsx', 'Sheet1', 'A9:Q9');
x=x';     %x进行转置 
y=y';     %y进行转置
%将y设置为0,1两类
y=y-1;
%获取输入参数的样本数与参数数
[m,d]=size(x);    %m是x矩阵的行数，表示总共有多少个训练集。d是矩阵的列数，表示训练集的输入。

OutputLayerNum=1;  %输出层神经元

v=rand(d,d+1);                      %输入层与隐层的权值,v是一个d行d+1列矩阵
w=rand(d+1,OutputLayerNum);         %隐层与输出层的权值,w是一个d+1行1列矩阵
gamma=rand(d+1);                    %隐层阈值,gamma是d+1行1列矩阵
theta=rand(OutputLayerNum);         %输出层阈值,theta是1行1列矩阵
py=zeros(m,OutputLayerNum);         %输出层输出
b=zeros(d+1);                       %隐层输出
g=zeros(OutputLayerNum);            %均方误差对w,gamma求导的参数
e=zeros(d+1);                       %均方误差对v,theta求导的参数

eta=1;                               %学习率

kn=0;        %迭代的次数
sn=0;        %同样的均方误差值累积次数
previous_E=0; %前一次迭代的累计误差
while(1)
    kn=kn+1;
    E=0;      %当前迭代的均方误差
    %计算全部样本输出层输出
    for i=1:m
      %计算隐层的输出
      for j=1:d+1
        alpha=0;
        for k=1:d
          alpha=alpha+v(k,j)*x(i,k);
        end
        b(i,j)=1/(1+exp(-alpha+gamma(j)));
       end
       %计算输出层输出
       for j=1:OutputLayerNum
         beta=0;
         for k=1:d+1
           beta=beta+w(k,j)*b(i,k);
          end
          py(i,j)=1/(1+exp(-beta+theta(j)));
         end
        end
       %用来存储累积误差对四个变量的下降方向
       delta_v=zeros(d,d+1);
       delta_w=zeros(d+1,OutputLayerNum);
       delta_gamma=zeros(d+1);
       delta_theta=zeros(OutputLayerNum);
       %计算累积误差
       for i=1:m
         for j=1:OutputLayerNum
           E=E+((y(i)-py(i,j))^2)/2;
          end
          %计算w、theta导数参数
          for j=1:OutputLayerNum
            g(j)=py(i,j)*(1-py(i,j))*(y(i)-py(i,j));
          end
          %计算v、gamma导数参数
          for j=1:d+1
            teh=0;
            for k=1:OutputLayerNum
              teh=teh+w(j,k)*g(k);
            end
              e(j)=teh*b(i,j)*(1-b(i,j));
          end
          %计算w、theta导数
          for j=1:OutputLayerNum
            delta_theta=delta_theta+(-1)*eta*g(j);
            for k=1:d+1
              delta_w(k,j)=delta_w(k,j)+eta*g(j)*b(i,k);
            end
          end
          %计算v、gamma导数
          for j=1:d+1
            gamma(j)= gamma(j)+(-1)*eta*e(j);
            for k=1:d
              delta_v(k,j)=delta_v(k,j)+eta*e(j)*x(i,k);
            end
           end
          end
          %更新参数
          v=v+delta_v;
          w=w+delta_w;
         gamma=gamma+delta_gamma;
         theta=theta+delta_theta;
         %迭代终止条件
         if(abs(previous_E-E)<0.0001)
            sn=sn+1;
            if(sn==50)
               break;
            end
          else
           previous_E=E;
           sn=0;
         end
end

训练的数据集还是西瓜数据集3.0,上边已经给出了。

训练权重的结果：