周志华版机器学习第三章习题答案

原文参考链接：[https://blog.csdn.net/icefire_tyh/article/details/52064910]
习题
3.1

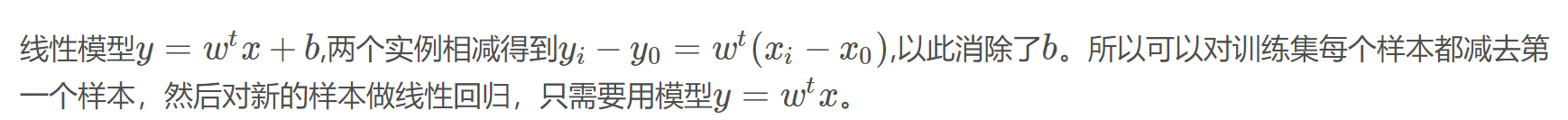
3.2
如果一个多元函数是凸的，那么它的Hessian矩阵是半正定的

3.3

#导入需要的包
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
#导入数据
data = np.array([[0.697, 0.460, 1],
        [0.774, 0.376, 1],
        [0.634, 0.264, 1],
        [0.608, 0.318, 1],
        [0.556, 0.215, 1],
        [0.403, 0.237, 1],
        [0.481, 0.149, 1],
        [0.437, 0.211, 1],
        [0.666, 0.091, 0],
        [0.243, 0.267, 0],
        [0.245, 0.057, 0],
        [0.343, 0.099, 0],
        [0.639, 0.161, 0],
        [0.657, 0.198, 0],
        [0.360, 0.370, 0],
        [0.593, 0.042, 0],
        [0.719, 0.103, 0]])
定义变量
X = data[:,0:2]
y = data[:,2]
#随机划分训练集和测试集
X_train,X_test,Y_train,Y_test=train_test_split(X,y,test_size=0.25,random_state=33)
 #定义sigmoid
def sigmoid(z): 
    s = 1 / (1 + np.exp(-z))
    return s
def initialize_with_zeros(dim):
    """
    This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
    """
    w = np.zeros((dim, 1))
    b = 0
    assert (w.shape == (dim, 1))
    assert (isinstance(b, float) or isinstance(b, int))
    return w, b

def propagate(w, b, X, Y):
    """
    Implement the cost function and its gradient for the propagation explained above
    """
    m = X.shape[1]
    A = sigmoid(np.dot(w.T, X) + b)
      # 计算损失
    cost = -np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))/ m  
  
    dw = np.dot(X, (A - Y).T) / m
    db = np.sum(A - Y) / m

    assert (dw.shape == w.shape)
    assert (db.dtype == float)
    cost = np.squeeze(cost)
    assert (cost.shape == ())

    grads = {"dw": dw,
             "db": db}
    return grads, cost

def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost=False):
    """
    This function optimizes w and b by running a gradient descent algorithm
    """
    costs = []

    for i in range(num_iterations):
        grads, cost = propagate(w, b, X, Y)
        # Retrieve derivatives from grads
        dw = grads["dw"]
        db = grads["db"]
        # update rule 
        w = w - learning_rate * dw
        b = b - learning_rate * db
        # Record the costs
        if i % 100 == 0:
            costs.append(cost)
        # Print the cost every 100 training iterations
        if print_cost and i % 100 == 0:
            print("Cost after iteration %i: %f" % (i, cost))

    params = {"w": w,
              "b": b}
    grads = {"dw": dw,
             "db": db}
    return params, grads, costs
def predict(w, b, X):
    '''
    Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
    '''
    m = X.shape[1]
    Y_prediction = np.zeros((1, m))
    w = w.reshape(X.shape[0], 1)

    # Compute vector "A" predicting the probabilities of a cat being present in the picture
    A = sigmoid(np.dot(w.T, X) + b)
    for i in range(A.shape[1]):
        # Convert probabilities A[0,i] to actual predictions p[0,i]
        if A[0, i] >= 0.5:
            Y_prediction[0, i] = 1
        else:
            Y_prediction[0, i] = 0
        pass
    assert (Y_prediction.shape == (1, m))

    return Y_prediction
def model(X_train, Y_train, X_test, Y_test, num_iterations, learning_rate, print_cost=False):
    # initialize parameters with zeros (≈ 1 line of code)
    w, b = initialize_with_zeros(X_train.shape[0])

    # Gradient descent (≈ 1 line of code)
    parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)

    # Retrieve parameters w and b from dictionary "parameters"
    w = parameters["w"]
    b = parameters["b"]

    # Predict test/train set examples (≈ 2 lines of code)
    Y_prediction_test = predict(w, b, X_test)
    Y_prediction_train = predict(w, b, X_train)

    # Print train/test Errors
    print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
    print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))

    d = {"costs": costs,
         "Y_prediction_test": Y_prediction_test,
         "Y_prediction_train": Y_prediction_train,
         "w": w,
         "b": b,
         "learning_rate": learning_rate,
         "num_iterations": num_iterations}

    return d
X_train = X_train.T
Y_train = Y_train.T.reshape(1,X_train.shape[1])
X_test = X_test.T
Y_test = Y_test.T.reshape(1,X_test.shape[1])
d = model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = True)
# Plot learning curve (with costs)
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()

显示结果


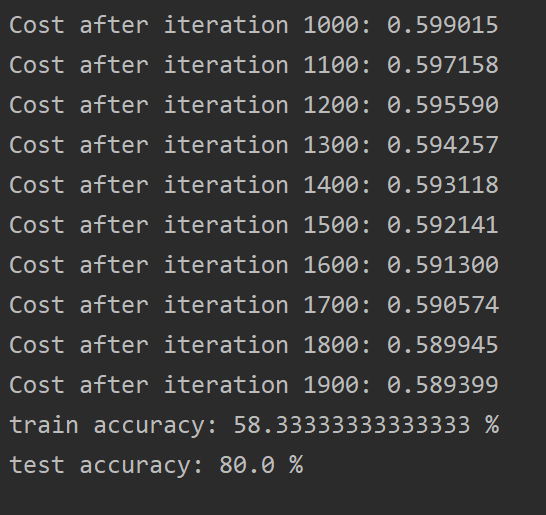
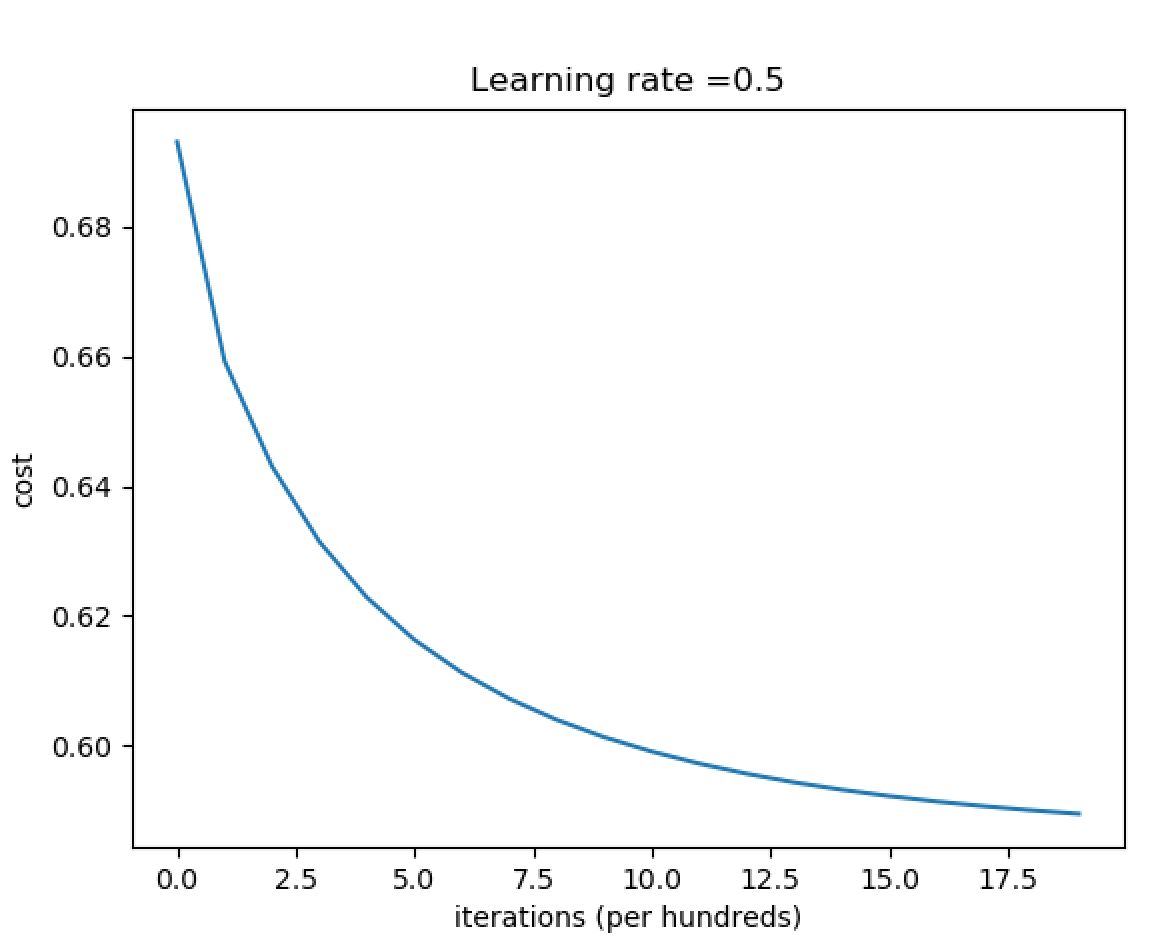
3.4

import numpy as np
import matplotlib.pyplot as plt

def readData():
    """
    Read data from txt file.
    Return:
        X1, y1, X2, y2, X3, y3: X is list with shape [50, 4],
                                y is list with shape [50,]
    """
    X1 = []
    y1 = []
    X2 = []
    y2 = []
    X3 = []
    y3 = []
    #read data from txt file
    with open("bezdekIris.txt", "r") as f:
        for line in f:
            x = []
            iris = line.strip().split(",")
            for attr in iris[0:4]:
                x.append(float(attr))

            if iris[4]=="Iris-setosa":
                X1.append(x)
                y1.append(1)
            elif iris[4]=="Iris-versicolor":
                X2.append(x)
                y2.append(2)
            else:
                X3.append(x)
                y3.append(3)
    return X1, y1, X2, y2, X3, y3

def tenFoldData(X1, X2):
    """
    Generate 10-fold training data. Each fold includes 5 positive and 5 negtive.
    Input:
        X1: list with shape [50, 4]. Instances in X1 belong to positive class.
        X2: list with shape [50, 4]. Instances in X2 belong to negtive class.
    Return:
        folds: list with shape [10, 10, 4].
        y: list with shape [10, 10]
    """
    print (len(X1))
    print (len(X2))
    folds = []
    y = []
    for i in range(10):
        fold = []
        fold += X1[ i*5:(i+1)*5 ]
        fold += X2[ i*5:(i+1)*5 ]
        folds.append(fold)
        y.append([1]*5 + [0]*5)
    return folds, y

def LR(X, y):
    """
    Given training dataset, return optimal params of LR algorithm with Newton method.
    Input:
        X: np.array with shape [N, d]. Input.
        y: np.array with shape [N, 1]. Label.
    Return:
        beta: np.array with shape [1, d]. Optimal params with Newton method
    """
    N, d = X.shape
    lr = 0.001
    #initialization
    beta = np.ones((1, d)) * 0.1
    #shape [N, 1]
    z = X.dot(beta.T)

    for i in range(150):
        #shape [N, 1]
        p1 = np.exp(z) / (1 + np.exp(z))
        #shape [N, N]
        p = np.diag((p1 * (1-p1)).reshape(N))
        #shape [1, d]
        first_order = -np.sum(X * (y - p1), 0, keepdims=True)

        #update
        beta -= first_order * lr
        z = X.dot(beta.T)

    l = np.sum(y*z + np.log( 1+np.exp(z) ) )
    #print l
    return beta


def testing(beta, X, y):
    """
    Given trained LR model, return error number in input X.
    Input:
        beta: np.array with shape [1, d]. params of LR model
        X: np.array with shape [N, d]. Testing instances.
        y: np.array with shape [N, 1]. Testing labels.
    Return:
        error_num: Error num of LR on X.
    """
    predicts = ( X.dot(beta.T) >= 0 )
    error_num = np.sum(predicts != y)
    return error_num

def tenFoldCrossValidation(folds, y):
    """
    Return erroe num of 10-fold cross validation.
    Input:
        folds: list with shape [10, 10, 4].
        y: list with shape [10, 10]
    Return:
        ten_fold_error_nums:
    """
    ten_fold_error_nums = 0
    for i in range(10):
        train_X = folds[:i] + folds[i+1:]
        train_y = y[:i] + y[i+1:]
        val_X = folds[i]
        val_y = y[i]
        train_X = np.array(train_X).reshape(-1, 4)
        train_y = np.array(train_y).reshape([-1, 1])
        val_X = np.array(val_X)
        val_y = np.array(val_y).reshape([-1, 1])
        beta = LR(train_X, train_y)
        error_num = testing(beta, val_X, val_y)
        ten_fold_error_nums += error_num
    return ten_fold_error_nums

def LOO(X, y):
    """
    Return erroe num of LOO.
    Input:
        X: list with shape [100, 4].
        y: list with shape [100]
    Return:
        loo_error_nums:
    """
    loo_error_nums = 0
    for i in range(100):
        train_X = X[:i] + X[i+1:]
        train_y = y[:i] + y[i+1:]
        val_X = X[i]
        val_y = y[i]
        train_X = np.array(train_X).reshape(-1, 4)
        train_y = np.array(train_y).reshape([-1, 1])
        val_X = np.array(val_X)
        val_y = np.array(val_y).reshape([-1, 1])
        beta = LR(train_X, train_y)
        error_num = testing(beta, val_X, val_y)
        loo_error_nums += error_num
    return loo_error_nums

if __name__=="__main__":
    #data read from txt file
    X1, y1, X2, y2, X3, y3 = readData()

    #10-fold cross validation
    print ("10-fold cross validation...")
    #X1 and X2
    folds, y = tenFoldData(X1, X2)
    round1_ten_fold_error_nums = tenFoldCrossValidation(folds, y)
    #X1, X3
    folds, y = tenFoldData(X1, X3)
    round2_ten_fold_error_nums = tenFoldCrossValidation(folds, y)
    #X2, X3
    folds, y = tenFoldData(X3, X2)
    round3_ten_fold_error_nums = tenFoldCrossValidation(folds, y)
    ten_fold_error_nums = round1_ten_fold_error_nums + round2_ten_fold_error_nums 
                          + round3_ten_fold_error_nums

    #LOO
    print ("LOO ...")
    #X1, X2
    X = X1 + X2
    y = [1]*len(X1) + [0]*len(X2)
    round1_loo_error_nums = LOO(X, y)
    #X1, X3
    X = X1 + X3
    y = [1]*len(X1) + [0]*len(X2)
    round2_loo_error_nums = LOO(X, y)
    #X2, X3
    X = X3 + X2
    y = [1]*len(X1) + [0]*len(X2)
    round3_loo_error_nums = LOO(X, y)
    loo_error_nums = round1_loo_error_nums + round2_loo_error_nums 
                     + round3_loo_error_nums
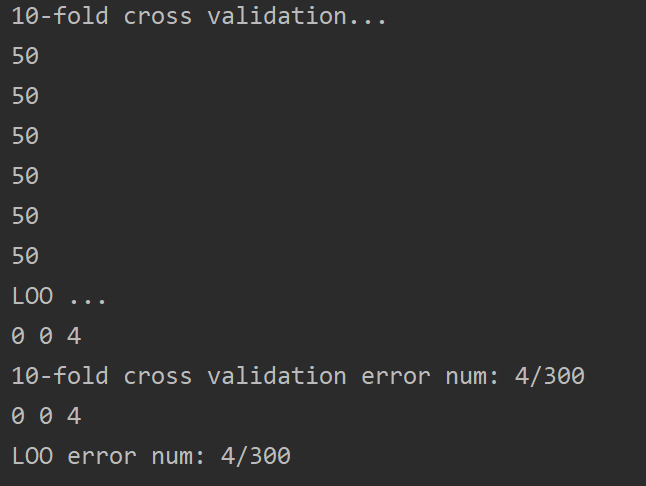
    print (round1_ten_fold_error_nums, round2_ten_fold_error_nums, round3_ten_fold_error_nums)
    print ("10-fold cross validation error num: {}/300".format(ten_fold_error_nums))
    print (round1_loo_error_nums, round2_loo_error_nums, round3_loo_error_nums)
    print ("LOO error num: {}/300".format(loo_error_nums))

3.5

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

def LDA(X0, X1):
    """
    Get the optimal params of LDA model given training data.
    Input:
        X0: np.array with shape [N1, d]
        X1: np.array with shape [N2, d]
    Return:
        omega: np.array with shape [1, d]. Optimal params of LDA.
    """
    #shape [1, d]
    mean0 = np.mean(X0, axis=0, keepdims=True)
    mean1 = np.mean(X1, axis=0, keepdims=True)
    Sw = (X0-mean0).T.dot(X0-mean0) + (X1-mean1).T.dot(X1-mean1)
    omega = np.linalg.inv(Sw).dot((mean0-mean1).T)
    return omega

if __name__=="__main__":
    #read data from xls
    work_book = pd.read_csv("watermelon_3a.csv", header=None)
    positive_data = work_book.values[work_book.values[:, -1] == 1.0, :]
    negative_data = work_book.values[work_book.values[:, -1] == 0.0, :]
    print (positive_data)

    #LDA
    omega = LDA(negative_data[:, 1:-1], positive_data[:, 1:-1])

    #plot
    plt.plot(positive_data[:, 1], positive_data[:, 2], "bo")
    plt.plot(negative_data[:, 1], negative_data[:, 2], "r+")
    lda_left = 0
    lda_right = -(omega[0]*0.9) / omega[1]
    plt.plot([0, 0.9], [lda_left, lda_right], 'g-')

    plt.xlabel('density')
    plt.ylabel('sugar rate')
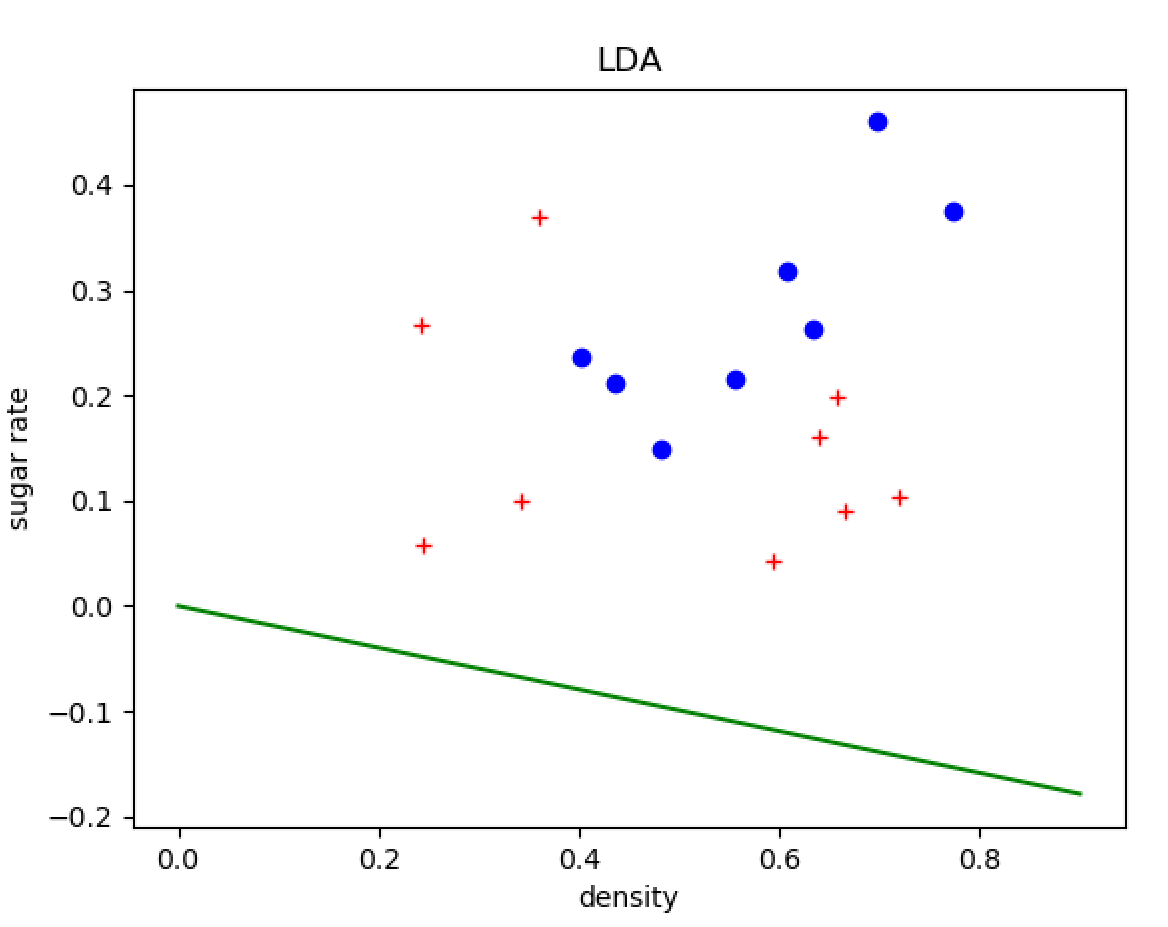
    plt.title("LDA")
    plt.show()

结果如下
[[1. 0.697 0.46 1. ]
[2. 0.774 0.376 1. ]
[3. 0.634 0.264 1. ]
[4. 0.608 0.318 1. ]
[5. 0.556 0.215 1. ]
[6. 0.403 0.237 1. ]
[7. 0.481 0.149 1. ]
[8. 0.437 0.211 1. ]]

3.6
参照6.4节，使用核函数, 就可以运用于非线性可分数据
3.7-3.10
略略略~
我也不会做，挖个坑在这，有时间再填

最后

以上就是生动刺猬为你收集整理的周志华版机器学习第三章习题答案的全部内容，希望文章能够帮你解决周志华版机器学习第三章习题答案所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。