特征降维是无监督学习的另一个应用,目的有两个:一是我们经常在实际项目中遭遇特征维度非常高的训练样本,而往往无法借助自己的领域知识人工构建有效特征;二是在数据表现方面,我们无法用肉眼观测超过三个维度的特征。因此特征降维不仅重构了有效的低维度特征向量,同时也为数据展现提供了可能。PCA是最为经典和实用的特征降维技术,特别在辅助图形识别方面有突出的表现。
本篇我们依然沿用上篇的“手写体数字图像”全集数据。我们从PCA展示数据的角度出发,显示经过处理之后,这些数字图像映射在二维空间的分布情况,如下图所示。
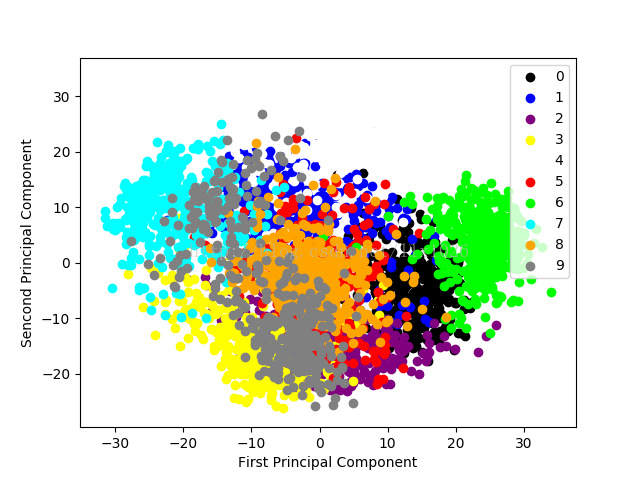
尽管我们把原始64维度的图像压缩到只有二个维度的特征空间,依然可以发现绝大多数数字之间的区分性,详细过程见如下代码:
# 导入pandas用于数据读取和处理。
import pandas as pd
# 从互联网读入手写体图片识别任务的训练数据,存储在变量digits_train中。
digits_train = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tra', header=None)
# 从互联网读入手写体图片识别任务的测试数据,存储在变量digits_test中。
digits_test = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tes', header=None)
# 分割训练数据的特征向量和标记。
X_digits = digits_train[np.arange(64)]
y_digits = digits_train[64]
# 从sklearn.decomposition导入PCA。
from sklearn.decomposition import PCA
# 初始化一个可以将高维度特征向量(64维)压缩至2个维度的PCA。
estimator = PCA(n_components=2)
X_pca = estimator.fit_transform(X_digits)
# 显示10类手写体数字图片经PCA压缩后的2维空间分布。
from matplotlib import pyplot as plt
def plot_pca_scatter():
colors = ['black', 'blue', 'purple', 'yellow', 'white', 'red', 'lime', 'cyan', 'orange', 'gray']
for i in xrange(len(colors)):
px = X_pca[:, 0][y_digits.as_matrix() == i]
py = X_pca[:, 1][y_digits.as_matrix()== i]
plt.scatter(px, py, c=colors[i])
plt.legend(np.arange(0,10).astype(str))
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.show()
plot_pca_scatter()我们在基础篇3中使用了支持向量机分类模型对手写体数字图像进行识别,并取得了很好的预测性能。当时,我们使用了64维度的图像像素特征对模型进行训练。这里我们通过下述代码,分别训练两个以支持向量机为基础的手写体数字图像识别模型,其中一个模型以原始64维度的像素特征,另一个采用经过PCA压缩重建之后的低维特征。
# 对训练数据、测试数据进行特征向量(图片像素)与分类目标的分隔。
X_train = digits_train[np.arange(64)]
y_train = digits_train[64]
X_test = digits_test[np.arange(64)]
y_test = digits_test[64]
# 导入基于线性核的支持向量机分类器。
from sklearn.svm import LinearSVC
# 使用默认配置初始化LinearSVC,对原始64维像素特征的训练数据进行建模,并在测试数据上做出预测,存储在y_predict中。
svc = LinearSVC()
svc.fit(X_train, y_train)
y_predict = svc.predict(X_test)
# 使用PCA将原64维的图像数据压缩到20个维度。
estimator = PCA(n_components=20)
# 利用训练特征决定(fit)20个正交维度的方向,并转化(transform)原训练特征。
pca_X_train = estimator.fit_transform(X_train)
# 测试特征也按照上述的20个正交维度方向进行转化(transform)。
pca_X_test = estimator.transform(X_test)
# 使用默认配置初始化LinearSVC,对压缩过后的20维特征的训练数据进行建模,并在测试数据上做出预测,存储在pca_y_predict中。
pca_svc = LinearSVC()
pca_svc.fit(pca_X_train, y_train)
pca_y_predict = pca_svc.predict(pca_X_test)使用下述代码对比原始维度特征与经过PCA压缩重建之后的图像特征在相同配置的支持向量机模型上识别性能的差异。
# 从sklearn.metrics导入classification_report用于更加细致的分类性能分析。
from sklearn.metrics import classification_report
# 对使用原始图像高维像素特征训练的支持向量机分类器的性能作出评估。
print svc.score(X_test, y_test)
print classification_report(y_test, y_predict, target_names=np.arange(10).astype(str))
# 对使用PCA压缩重建的低维图像特征训练的支持向量机分类器的性能作出评估。
print pca_svc.score(pca_X_test, y_test)
print classification_report(y_test, pca_y_predict, target_names=np.arange(10).astype(str))0.930996104619
precision recall f1-score support
0 0.99 0.98 0.99 178
1 0.94 0.84 0.89 182
2 0.99 0.97 0.98 177
3 0.97 0.92 0.94 183
4 0.95 0.97 0.96 181
5 0.89 0.96 0.93 182
6 0.99 0.98 0.99 181
7 0.98 0.90 0.94 179
8 0.78 0.91 0.84 174
9 0.86 0.89 0.87 180
avg / total 0.93 0.93 0.93 1797
0.909293266555
precision recall f1-score support
0 0.96 0.96 0.96 178
1 0.78 0.85 0.82 182
2 0.96 0.98 0.97 177
3 0.99 0.89 0.94 183
4 0.95 0.92 0.93 181
5 0.84 0.97 0.90 182
6 0.96 0.97 0.96 181
7 0.93 0.92 0.93 179
8 0.83 0.83 0.83 174
9 0.92 0.82 0.86 180
avg / total 0.91 0.91 0.91 1797
我们发现,尽管经过PCA特征压缩和重建之后的特征数据会损失2%左右的预测准确性,但是相比原始数据的特征而言,我们使用PCA压缩了并降低了68.75%的维度。
特点分析:降维/压缩问题则是选取数据具有代表性的特征,在保持数据多样性的基础上,规避掉大龙的特征冗余和噪声,不过这个过程也很有可能会损失一些有用的模式信息。经过大量的实践证明,相较于损失的少部分模型性能,维度压缩能够节省大量用于模型训练的实践。这样一来,使得PCA所带来的模型综合效率变得更为划算。
最后
以上就是从容绿草最近收集整理的关于Python机器学习及实践——特征降维的全部内容,更多相关Python机器学习及实践——特征降维内容请搜索靠谱客的其他文章。








发表评论 取消回复