Feature Selection and Extraction

Reference:

Pattern recognition, by Sergios Theodoridis, Konstantinos Koutroumbas (2009)

Slides of CS4220, TUD

The Peaking Phenomenon (5.3)

More features $\stackrel{?}{⟹}$ Better performance

• If the corresponding PDFs are known, the Bayesian error goes down with more features. We can perfectly discriminate the two classes by arbitrarily increasing the number of features.
• If the PDFs are unknown and the associated parameters must be estimated using a finite training set, then we must try to keep the number of features to a relatively low number.

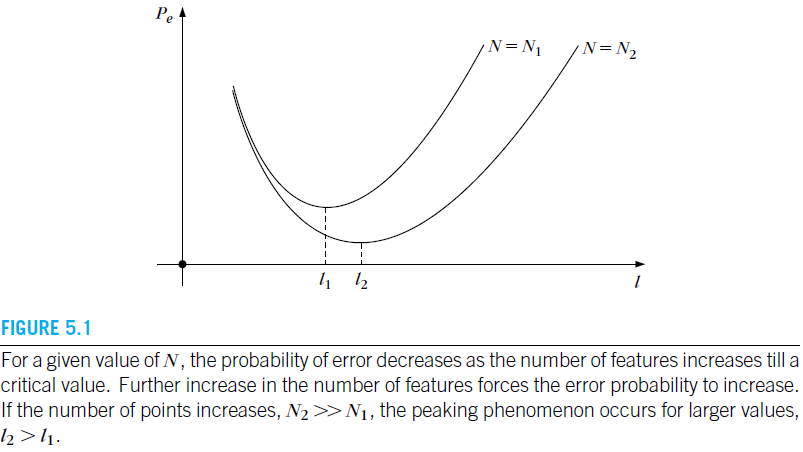
In practice, for a finite $N$, by increasing the number of features one obtains an initial improvement in performance, but after a critical value further increase of the number of features results in an increase of the probability of error. This phenomenon is also known as the peaking phenomenon.

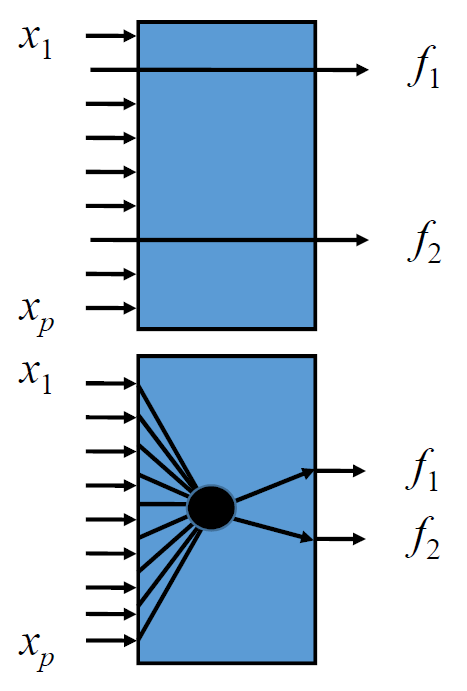
What feature subset to keep? $⟹$ Feature selection / extraction

• Feature selection: select $d$ out of $p$ measurements
• Feature extraction: map $p$ measurements to $d$ measurements

What do we need?

• Criterion functions, e.g., error, class overlap, information loss…
• Optimization or “search” algorithms to find mapping for given criterion

Class Separability Measures (5.6)

Divergence

Let us recall our familiar Bayes rule. Given two classes ${\omega }_1$ and ${\omega }_2$ and a feature vector $\mathbf{x}$, we select ${\omega }_1$ if
$$P({\omega }_1|\mathbf{x})>P({\omega }_2|\mathbf{x})$$
The classification error probability depends on the difference between $P({\omega }_1|\mathbf{x})$ and $P({\omega }_2|\mathbf{x})$, hence the ratio $P({\omega }_1|\mathbf{x})/P({\omega }_2|\mathbf{x})$ can convey useful information concerning the discriminatory capabilities associated with an adopted feature vector $\mathbf{x}$. Alternatively, the same information resides in the ratio
$$\ln \frac{p(\mathbf{x}|{\omega }_1)}{p(\mathbf{x}|{\omega }_2)}\equiv D_{12}(\mathbf{x})$$
Since $\mathbf{x}$ takes different values, it is natural to consider the mean value over class ${\omega }_1$ (because $\mathbf{x}$ is classified to class ${\omega }_1$), that is
$$D_{12}={\int }_{-\infty }^{+\infty }p(\mathbf{x}|{\omega }_1)\ln \frac{p(\mathbf{x}|{\omega }_1)}{p(\mathbf{x}|{\omega }_2)}d\mathbf{x}\text{\hspace{1em}(DV.1)}$$
Similar arguments hold for class ${\omega }_2$, and we define
$$D_{21}={\int }_{-\infty }^{+\infty }p(\mathbf{x}|{\omega }_2)\ln \frac{p(\mathbf{x}|{\omega }_2)}{p(\mathbf{x}|{\omega }_1)}d\mathbf{x}\text{\hspace{1em}(DV.2)}$$
The sum
$$d_{12}=D_{12}+D_{21}\text{\hspace{1em}(DV.3)}$$
is known as the divergence and can be used as a separability measure for the classes ${\omega }_1,{\omega }_2$, with respect to the adopted feature vector $\mathbf{x}$.

For a multiclass problem, the divergence is computed for every class pair ${\omega }_i,{\omega }_j$
$$d_{ij}=D_{ij}+D_{ji}={\int }_{-\infty }^{+\infty }[p(\mathbf{x}|{\omega }_i)-p(\mathbf{x}|{\omega }_j)]\ln \frac{p(\mathbf{x}|{\omega }_i)}{p(\mathbf{x}|{\omega }_j)}d\mathbf{x}\text{\hspace{1em}(DV.4)}$$
and the average class separability can be computed using the average divergence
$$d=\sum _{i=1}^M\sum _{j=1}^{M}P({\omega }_i)P({\omega }_j)d_{ij}\text{\hspace{1em}(DV.5)}$$
If the components of the feature vector are statistically independent, then it can be shown that
$$\begin{array}{rl}{d}_{ij}(x_1,x_2,\cdots ,x_l)& ={\int }_{-\infty }^{+\infty }[p(\mathbf{x}|{\omega }_i)-p(\mathbf{x}|{\omega }_j)]\sum _{r=1}^l\ln \frac{p(x_r|{\omega }_i)}{p(x_r|{\omega }_j)}d\mathbf{x}\\ & \stackrel{a}{=}\sum _{r=1}^l{\int }_{-\infty }^{+\infty }[p(x_r|{\omega }_i)-p(x_r|{\omega }_j)]\ln \frac{p(x_r|{\omega }_i)}{p(x_r|{\omega }_j)}d{x}_r\\ & =\sum _{r=1}^l{d}_{ij}(x_r)\end{array}\text{\hspace{1em}(DV.6)}$$
where $\stackrel{a}{=}$ is due to
$${\int }_{-\infty }^{+\infty }\cdots {\int }_{-\infty }^{+\infty }p(\mathbf{x}|{\omega }_i)-p(\mathbf{x}|{\omega }_j)d{x}_1\cdots d{x}_{r-1}d{x}_{r+1}\cdots d{x}_l=p(x_r|{\omega }_i)-p(x_r|{\omega }_j)$$
Assuming now that the density functions are Gaussians $\mathcal{N}({\mathbf{\mu }}_i,{\mathbf{\Sigma }}_i)$ and $\mathcal{N}({\mathbf{\mu }}_j,{\mathbf{\Sigma }}_j)$, respectively, the computation of the divergence is simplified, and it is not difficult to show that
d i j = 1 2 t r a c e { Σ i − 1 Σ j + Σ j − 1 Σ i − 2 I } + 1 2 ( μ i − μ j ) T ( Σ i − 1 + Σ j − 1 ) ( μ i − μ j ) (DV.7) d_{ij}=frac{1}{2}mathrm{trace}{boldsymbol Sigma_i^{-1}boldsymbol Sigma_j+boldsymbol Sigma_j^{-1}boldsymbol Sigma_i-2I }+frac{1}{2}(boldsymbol mu_i-boldsymbol mu_j)^T(boldsymbol Sigma_i^{-1}+boldsymbol Sigma_j^{-1})(boldsymbol mu_i-boldsymbol mu_j)tag{DV.7} dij​=21​trace{Σi−1​Σj​+Σj−1​Σi​−2I}+21​(μi​−μj​)T(Σi−1​+Σj−1​)(μi​−μj​)(DV.7)
It can be seen that a class separability measure cannot depend only on the difference of the mean values; it must also be variance dependent. If the covariance matrices of the two Gaussian distributions are equal, then the divergence is further simplified to
$$d_{ij}=({\mathbf{\mu }}_i-{\mathbf{\mu }}_j{)}^T{\mathbf{\Sigma }}^{-1}({\mathbf{\mu }}_i-{\mathbf{\mu }}_j)$$
which is nothing other than the Mahalanobis distance between the corresponding mean vectors. This has a direct relation with the Bayes error, which is a desirable property for class separation measures.

Chernoff Bound and Bhattacharyya Distance

The minimum attainable classification error of the Bayes classifier for two classes ${\omega }_1,{\omega }_2$ can be written as
$$P_e={\int }_{-\infty }^{+\infty }\min [P({\omega }_i)p(\mathbf{x}|{\omega }_i),P({\omega }_j)p(\mathbf{x}|{\omega }_j)]d\mathbf{x}\text{\hspace{1em}(CB.1)}$$
Analytic computation of this integral in the general case is not possible. However, an upper bound can be derived based on the inequality
$$\min [a,b]\le a^s{b}^{1-s}\text{for }a,b\ge 0,\text{ and }0\le s\le 1\text{\hspace{1em}(CB.2)}$$
Combining $(CB.1)$ and $(CB.2)$, we get
$$P_e\le P({\omega }_i{)}^{s}P({\omega }_j{)}^{1-s}{\int }_{-\infty }^{+\infty }p(\mathbf{x}|{\omega }_i{)}^{s}p(\mathbf{x}|{\omega }_j{)}^{1-s}d\mathbf{x}\equiv {ϵ}_{CB}\text{\hspace{1em}(CB.3)}$$
${ϵ}_{CB}$ is known as the Chernoff bound. The minimum bound can be computed by minimizing ${ϵ}_{CB}$ w.r.t $s$.

A special form of the bound results for $s=1/2$. For Gaussian distributions $\mathcal{N}({\mathbf{\mu }}_i,{\mathbf{\Sigma }}_i)$ and $\mathcal{N}({\mathbf{\mu }}_j,{\mathbf{\Sigma }}_j)$, it reduces to
$${ϵ}_{CB}=\sqrt{P({\omega }_i)P({\omega }_j)}\exp (-B)$$
where
$$B=\frac{1}{8}({\mathbf{\mu }}_i-{\mathbf{\mu }}_j{)}^T{\left(\frac{{\mathbf{\Sigma }}_i+{\mathbf{\Sigma }}_j}{2}\right)}^{-1}({\mathbf{\mu }}_i-{\mathbf{\mu }}_j)+\frac{1}{2}\ln \frac{\left|\frac{{\mathbf{\Sigma }}_i+{\mathbf{\Sigma }}_j}{2}\right|}{\sqrt{|{\mathbf{\Sigma }}_i||{\mathbf{\Sigma }}_j|}}\text{\hspace{1em}(CB.4)}$$
which is known as the Bhattacharyya distance.

Scatter Matrices

A major disadvantage of the class separability criteria considered so far is that they are not easily computed,unless the Gaussian assumption is employed. We will now turn our attention to a set of simpler criteria, built upon information related to the way feature vector samples are scattered in the $l$-dimensional space. To this end, the following matrices are defined:

• Within-class scatter matrix
  $${\mathbf{S}}_w=\sum _{i=1}^M{P}_i{\mathbf{\Sigma }}_i\text{\hspace{1em}(SM.1)}$$
  where ${\mathbf{\Sigma }}_i$ is the covariance matrix for class ${\omega }_i$
  $${\mathbf{\Sigma }}_i=E[(\mathbf{x}-{\mathbf{\mu }}_i)(\mathbf{x}-{\mathbf{\mu }}_i{)}^T]\simeq \frac{{\sum }_{\mathbf{x}\in {\omega }_i}\mathbf{x}{\mathbf{x}}^T}{n_i}-{\mathbf{\mu }}_i{\mathbf{\mu }}_i^T$$
  and $P_i$ is the priori probability of class ${\omega }_i$. That is, $P_i\simeq n_i/N$, where $n_i$ is the number of samples in class ${\omega }_i$, out of a total of $N$ samples.

• Between-class scatter matrix
  $${\mathbf{S}}_b=\sum _{i=1}^M{P}_i({\mathbf{\mu }}_i-{\mathbf{\mu }}_0)({\mathbf{\mu }}_i-{\mathbf{\mu }}_0{)}^T\text{\hspace{1em}(SM.2)}$$
  where ${\mathbf{\mu }}_0$ is the global mean vector
  $${\mathbf{\mu }}_0=\sum _i^M{P}_i{\mathbf{\mu }}_i$$

• Mixture scatter matrix
  $${\mathbf{S}}_m=E\left[\left(\mathbf{x}-{\mathbf{\mu }}_0\right){\left(\mathbf{x}-{\mathbf{\mu }}_0\right)}^T\right]\simeq \frac{\sum \mathbf{x}{\mathbf{x}}^T}{N}-{\mathbf{\mu }}_0{\mathbf{\mu }}_0^T\text{\hspace{1em}(SM.3)}$$

  That is, ${\mathbf{S}}_m$ is the covariance matrix of the feature vector with respect to the global mean. It can be shown that (with ${\mathbf{\mu }}_0={\sum }_i^M{P}_i{\mathbf{\mu }}_i$)
  $${\mathbf{S}}_m={\mathbf{S}}_w+{\mathbf{S}}_b\text{\hspace{1em}(SM.4)}$$

From these definitions it is straightforward to see that the criterion
J 1 = trace ⁡ { S m } trace ⁡ { S w } (SM.5) J_{1}=frac{operatorname{trace}left{mathbf S_{m}right}}{operatorname{trace}left{mathbf S_{w}right}}tag{SM.5} J1​=trace{Sw​}trace{Sm​}​(SM.5)
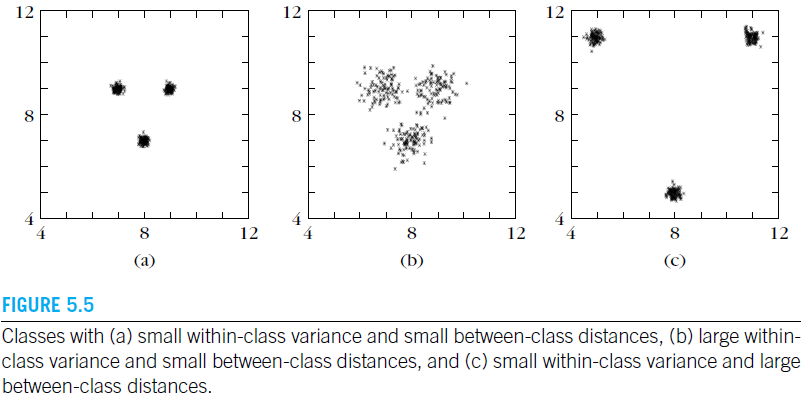
takes large values when samples in the $l$-dimensional space are well clustered around their mean, within each class, and the clusters of the different classes are well separated. Sometimes ${\mathbf{S}}_b$ is used in place of ${\mathbf{S}}_m$.

An alternative criterion results if determinants are used in the place of traces. This is justified for scatter matrices that are symmetric positive definite, and thus their eigenvalues are positive. The trace is equal to the sum of the eigenvalues, while the determinant is equal to their product. Hence, large values of $J_1$ also correspond to large values of the criterion
$$J_2=\frac{|{\mathbf{S}}_m|}{|{\mathbf{S}}_w|}=|{\mathbf{S}}_w^{-1}{\mathbf{S}}_m|\text{\hspace{1em}(SM.6)}$$
or
J 3 = t r a c e { S w − 1 S m } (SM.7) J_3=mathrm{trace}{mathbf S_w^{-1}mathbf S_m}tag{SM.7} J3​=trace{Sw−1​Sm​}(SM.7)
These criteria take a special form in the one-dimensional, two-class problem. In this case,it is easy to see that for equiprobable classes $|{\mathbf{S}}_w|$ is proportional to ${\sigma }_1^2+{\sigma }_2^2$ and $|{\mathbf{S}}_b|$ proportional to $({\mu }_1-{\mu }_2{)}^2$. Using $J_2$ leads to the so-called Fisher’s discriminant ratio (FDR) results
$$FDR=\frac{({\mu }_1-{\mu }_2{)}^2}{{\sigma }_1^2+{\sigma }_2^2}\text{\hspace{1em}(SM.8)}$$

Feature Selection (5.7)

The object is to select a subset of $l$ out of $m$ measurements which optimizes chosen criterion. Theoretically, there are $C_m^l=\frac{m!}{l!(m-l)!}$ subsets to be compared. Since the computation may not affordable in high dimension, we settle for suboptimal searching techniques.

The simplest way, named scalar feature selection, treats features individually. The value of the criterion $C(k)$ is computed for each of the features, $k=1,2,...,m$. The $l$ features corresponding to the $l$ best values of $C(k)$ are then selected to form the feature vector.

However, such approaches do not take into account existing correlations between features. Therefore, we proceed to techniques dealing with vectors, named vector feature selection.

Sequential Backward Selection

Starting from $m$, at each step we drop out one feature from the “best” combination until we obtain a vector of $l$ features.

For example, let $m=4$, and the originally available features are $x_1,x_2,x_3,x_4.$ We wish to select two of them. The selection procedure consists of the following steps:

• Adopt a class separability criterion, $C,$ and compute its value for the feature vector ${\left[x_1,x_2,x_3,x_4\right]}^T$
• Eliminate one feature and for each of the possible resulting combinations, that is, ${\left[x_1,x_2,x_3\right]}^T,{\left[x_1,x_2,x_4\right]}^T,{\left[x_1,x_3,x_4\right]}^T,{\left[x_2,x_3,x_4\right]}^T,$ compute the corresponding criterion value. Select the combination with the best value, say ${\left[x_1,x_2,x_3\right]}^T$
• From the selected three-dimensional feature vector eliminate one feature and for each of the resulting combinations, ${\left[x_1,x_2\right]}^T,{\left[x_1,x_3\right]}^T,{\left[x_2,x_3\right]}^T,$ compute the criterion value and select the one with the best value.

Sequential Forward Selection

Here, the reverse to the preceding procedure is followed:

• Compute the criterion value for each of the features. Select the feature with the best value, say $x_1$
• Form all possible two-dimensional vectors that contain the winner from the previous step, that is, ${\left[x_1,x_2\right]}^T,{\left[x_1,x_3\right]}^T,{\left[x_1,x_4\right]}^T$. Compute the criterion value for each of them and select the best one, say ${\left[x_1,x_3\right]}^T$.

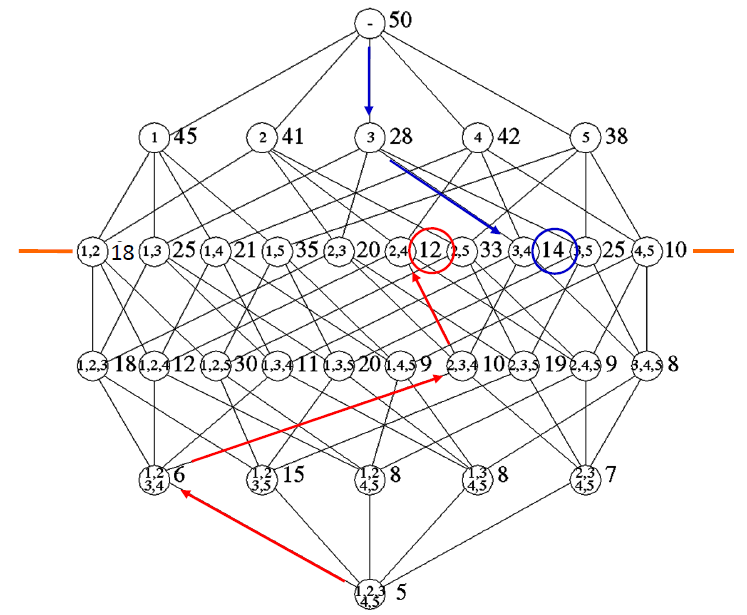
This figure shows how to select 2 out of 5 features using backward selection (red arrows) and forward selection (blue arrows). The black lines show all combinations needed to be computed if we want to find the optimal solution.

Note: Here we choose lower values, but sometimes we choose larger values, depending on the specific criterion.

Floating Search Methods

The $k+1$ best subset $X_{k+1}$ is formed by “borrowing” an element from $Y_{m-k}$. Then, return to the previously selected lower dimension subsets to check whether the inclusion of this new element improves the criterion $C$. If it does,the new element replaces one of the previously selected features.

Feature Extraction

We are going to introduce two classical linear feature extractors: LDA and PCA.

Let our data points, $\mathbf{x}$, be in the $m$-dimensional space and assume that they originate from two classes. Our goal is to generate a feature $\mathbf{y}$ as a linear combination of the components of $\mathbf{x}$. In such a way, we expect to “squeeze” the classification related information residing in $\mathbf{x}$ in a smaller number of features.

Supervised-Linear Discriminant Analysis-LDA (5.8)

In this section, this goal is achieved by seeking the direction $\mathbf{w}$ in the $m$ dimensional space, along which the two classes are best separated in some way.

Given an $\mathbf{x}\in {\mathcal{R}}^m$ the scalar
$$y=\frac{{\mathbf{w}}^T\mathbf{x}}{\Vert \mathbf{w}\Vert }\text{\hspace{1em}(LDA.1)}$$
is the projection of $\mathbf{x}$ along $\mathbf{w}$. Since scaling all our feature vectors by the same factor does not add any classification-related information, we will ignore the scaling factor $\Vert \mathbf{w}\Vert$.

For one dimensional, two-class problem, we can adopt the [Fisher’s discriminant ratio (FDR)](# Scatter Matrices)
$$FDR=\frac{({\mu }_1-{\mu }_2{)}^2}{{\sigma }_1^2+{\sigma }_2^2}\text{\hspace{1em}(SM.8)}$$
where ${\mu }_1,{\mu }_2$ are the mean values and ${\sigma }_1^2,{\sigma }_2^2$ the variances of $y$ in the two classes ${\omega }_1$ and ${\omega }_2$, respectively, after the projection along $\mathbf{w}$. Using the definition in $(LDA.1)$ and omitting $\Vert \mathbf{w}\Vert$, it is readily seen that
$${\mu }_i={\mathbf{w}}^T{\mathbf{\mu }}_i\text{\hspace{1em}(LDA.2)}$$
where ${\mathbf{\mu }}_i$ is the mean value of the data in ${\omega }_i$ in the $m$-dimensional space. Assuming the classes to be equiprobable and recalling the definition of ${\mathbf{S}}_b$ and ${\mathbf{S}}_w$ in [Scatter Matrices](# Scatter Matrices), it is easily shown that
$$({\mu }_1-{\mu }_2{)}^2={\mathbf{w}}^T({\mathbf{\mu }}_1-{\mathbf{\mu }}_2)({\mathbf{\mu }}_1-{\mathbf{\mu }}_2{)}^T\mathbf{w}\propto {\mathbf{w}}^T{\mathbf{S}}_b\mathbf{w}\text{\hspace{1em}(LDA.3)}$$

$${\sigma }_i^2=E[(y-{\mu }_i{)}^2]=E[{\mathbf{w}}^T(\mathbf{x}-{\mathbf{\mu }}_i)(\mathbf{x}-{\mathbf{\mu }}_i{)}^T\mathbf{w}]={\mathbf{w}}^T{\mathbf{\Sigma }}_i\mathbf{w}$$

$${\sigma }_1^2+{\sigma }_2^2\propto {\mathbf{w}}^T{\mathbf{S}}_w\mathbf{w}\text{\hspace{1em}(LDA.4)}$$

Combining $(SM.8)$, $(LDA.3)$, and $(LDA.4)$, we end up that the optimal direction is obtained by maximizing Fisher’s criterion
$$FDR(\mathbf{w})=\frac{{\mathbf{w}}^T{\mathbf{S}}_b\mathbf{w}}{{\mathbf{w}}^T{\mathbf{S}}_w\mathbf{w}}\text{\hspace{1em}(LDA.5)}$$
w.r.t. $\mathbf{w}$. This is celebrated generalized Rayleigh quotient. Since ${\mathbf{S}}_w$ is positive definite and symmetric (assuming ${\mathbf{S}}_w$ is invertible), let ${\mathbf{S}}_w=\mathbf{D}\mathbf{D}$ and $\mathbf{v}=\mathbf{D}\mathbf{w}$. Then
$$FDR(\mathbf{v})=\frac{{\mathbf{v}}^T{\mathbf{D}}^{-1}{\mathbf{S}}_b{\mathbf{D}}^{-1}\mathbf{v}}{{\mathbf{v}}^T\mathbf{v}}$$
It is maximized if $\mathbf{v}$ is chosen such that
$${\mathbf{D}}^{-1}{\mathbf{S}}_b{\mathbf{D}}^{-1}\mathbf{v}=\lambda \mathbf{v}$$
or in terms of $\mathbf{w}$,
$${\mathbf{S}}_w^{-1}{\mathbf{S}}_b\mathbf{w}=\lambda \mathbf{w}\text{\hspace{1em}(LDA.6)}$$
where $\lambda$ is the largest eigenvalue of ${\mathbf{S}}_w^{-1}{\mathbf{S}}_b$.

However, for our simple case we do not have to worry about any eigen decomposition. By the definition of ${\mathbf{S}}_b$ we have that
$$\lambda {\mathbf{S}}_w\mathbf{w}=({\mathbf{\mu }}_1-{\mathbf{\mu }}_2)({\mathbf{\mu }}_1-{\mathbf{\mu }}_2{)}^T\mathbf{w}=\alpha ({\mathbf{\mu }}_1-{\mathbf{\mu }}_2)$$
where $\alpha$ is a scalar. Solving the previous equation w.r.t. $\mathbf{w}$, and since we are only interested in the direction of $\mathbf{w}$, we can write
$$\mathbf{w}={\mathbf{S}}_w^{-1}({\mathbf{\mu }}_1-{\mathbf{\mu }}_2)\text{\hspace{1em}(LDA.7)}$$

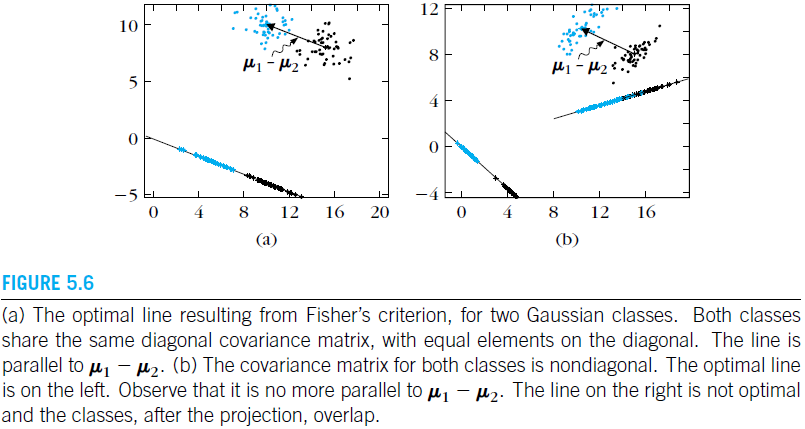
Thus, we have reduced the number of features from $m$ to $1$ in an optimal way. Classification can now be performed based on $y$. The resulting classifier is
$$g(\mathbf{x})=y+w_0=({\mathbf{\mu }}_1-{\mathbf{\mu }}_2{)}^T{\mathbf{S}}_w^{-1}\mathbf{x}+w_0\text{\hspace{1em}(LDA.8)}$$
It can be interpreted in two ways. Firstly, after the projection we got a scalar $y$. Compare it to some threshold $w_0$ and decide which class it belongs to. Secondly, we can omit the projection procedure and simply view $g(\mathbf{x})$ as a boundary which is perpendicular to $\mathbf{w}$.

However, the threshold $w_0$ is not provided by Fisher’s condition and has to be determined. For example, for the case of two Gaussian classes with the same covariance matrix the optimal classifier is shown to take the form
$$g(\mathbf{x})={\left({\mathbf{\mu }}_1-{\mathbf{\mu }}_2\right)}^T{\mathbf{S}}_w^{-1}\left(\mathbf{x}-\frac{1}{2}\left({\mathbf{\mu }}_1+{\mathbf{\mu }}_2\right)\right)-\ln \frac{P\left({\omega }_2\right)}{P\left({\omega }_1\right)}$$

Unsupervised-Principal Component Analysis-PCA (6.3)

In LDA, the class labels of the feature vectors were assumed known, and this information was optimally exploited to compute the transformation matrix. In PCA, however, we do not know the class labels of feature vectors. The transformation matrix will exploit the statistical information describing the data instead.

Karhunen–Loève (KL) transform

We assume that the data samples have zero mean. A desirable property of the generated features is to be mutually uncorrelated in an effort to avoid information redundancies. Therefore, we begin this section by first developing a method that generates mutually uncorrelated features, that is, $E[y(i)y(j)]=0,i\ne j$.

Let
$$\mathbf{y}={\mathbf{A}}^T\mathbf{x}\text{\hspace{1em}(PCA.1)}$$
Since we have assumed that $E[\mathbf{x}]=0$, it is readily seen that $E[\mathbf{y}]=0$. From the definition of the correlation matrix we have
$${\mathbf{R}}_y=E[\mathbf{y}{\mathbf{y}}^T]={\mathbf{A}}^T{\mathbf{R}}_x\mathbf{A}\text{\hspace{1em}(PCA.2)}$$
In practice, ${\mathbf{R}}_x$ is estimated as an average over the given set of training vectors.

Note that ${\mathbf{R}}_x$ is a symmetric matrix, and hence its eigenvectors are mutually orthogonal. Thus, if matrix $\mathbf{A}$ is chosen so that its columns are the orthonormal eigenvectors ${\mathbf{a}}_i,i=0,1,\dots ,N-1,$ of ${\mathbf{R}}_x,$ then ${\mathbf{R}}_y$ is diagonal
$${\mathbf{R}}_y={\mathbf{A}}^T{\mathbf{R}}_x\mathbf{A}=\mathbf{\Lambda }\text{\hspace{1em}(PCA.3)}$$
where $\mathbf{\Lambda }$ is the diagonal matrix having as elements on its diagonal the respective eigenvalues ${\lambda }_i,i=0,1,\dots ,N-1,$ of ${\mathbf{R}}_x$. Furthermore, assuming ${\mathbf{R}}_x$ to be positive definite so the eigenvalues are positive. The resulting transform is known as the Karhunen–Loève (KL) transform, and it achieves our original goal of generating mutually uncorrelated features.

Although our starting point was to generate mutually uncorrelated features, the KL transform turns out to have a number of other important properties, which provide different ways for its interpretation and also the secret for its popularity.

Mean Square Error Approximation

Since $\mathbf{A}$ is unitary, from $(PCA.1)$ we have $\mathbf{A}\mathbf{y}=\mathbf{x}$, or
$$\mathbf{x}=\sum _{i=0}^{N-1}y(i){\mathbf{a}}_i\text{and}y(i)={\mathbf{a}}_i^T\mathbf{x}\text{\hspace{1em}(PCA.4)}$$
To reduce the dimension, let us now define a new vector in the $m$-dimensional subspace
$$\hat{\mathbf{x}}=\sum _{i=0}^{m-1}y(i){\mathbf{a}}_i\text{\hspace{1em}(PCA.5)}$$
where only $m$ of the basis vectors are involved. Obviously, this is nothing but the projection of $\mathbf{x}$ onto the subspace spanned by the $m$ (orthonormal) eigenvectors involved in the summation. If we try to approximate $\mathbf{x}$ by its projection $\hat{\mathbf{x}},$ the resulting mean square error is given by
$$E\left[\Vert \mathbf{x}-\hat{\mathbf{x}}{\Vert }^2\right]=E\left[{\Vert \sum _{i=m}^{N-1}y(i){\mathbf{a}}_i\Vert }^2\right]\text{\hspace{1em}(PCA.6)}$$
Our goal now is to choose the eigenvectors that result in the minimum MSE. From $(PCA.6)$ and taking into account the orthonormality property of the eigenvectors, we have
$$\begin{array}{rl}E\left[{\Vert \sum _{i=m}^{N-1}y(i){\mathbf{a}}_i\Vert }^2\right]& =E\left[\sum _i\sum _j\left(y(i){\mathbf{a}}_i^T\right)\left(y(j){\mathbf{a}}_j\right)\right]\\ & =\sum _{i=m}^{N-1}E\left[y^2(i)\right]=\sum _{i=m}^{N-1}{\mathbf{a}}_i^{T}E\left[\mathbf{x}{\mathbf{x}}^T\right]{\mathbf{a}}_i\end{array}\text{\hspace{1em}(PCA.7)}$$
Using the eigenvector definition, we finally get
$$E\left[\Vert \mathbf{x}-\hat{\mathbf{x}}{\Vert }^2\right]=\sum _{i=m}^{N-1}{\mathbf{a}}_i^T{\lambda }_i{\mathbf{a}}_i=\sum _{i=m}^{N-1}{\lambda }_i\text{\hspace{1em}(PCA.8)}$$
Thus, if we choose in $(PCA.5)$ the eigenvectors corresponding to the $m$ largest eigenvalues of the correlation matrix, then the error in $(PCA.8)$ is minimized, being the sum of the $N-m$ smallest eigenvalues.

Total Variance

Since
$$\sum _{i=m}^{N-1}{\sigma }_{y(i)}^2=\sum _{i=m}^{N-1}E\left[y^2(i)\right]=\sum _{i=m}^{N-1}{\mathbf{a}}_i^{T}E\left[\mathbf{x}{\mathbf{x}}^T\right]{\mathbf{a}}_i=\sum _{i=m}^{N-1}{\mathbf{a}}_i^T{\lambda }_i{\mathbf{a}}_i=\sum _{i=m}^{N-1}{\lambda }_i\text{\hspace{1em}(PCA.9)}$$
we can see that the selected $m$ features retain most of the total variance associated with the original random variables $x(i)$.

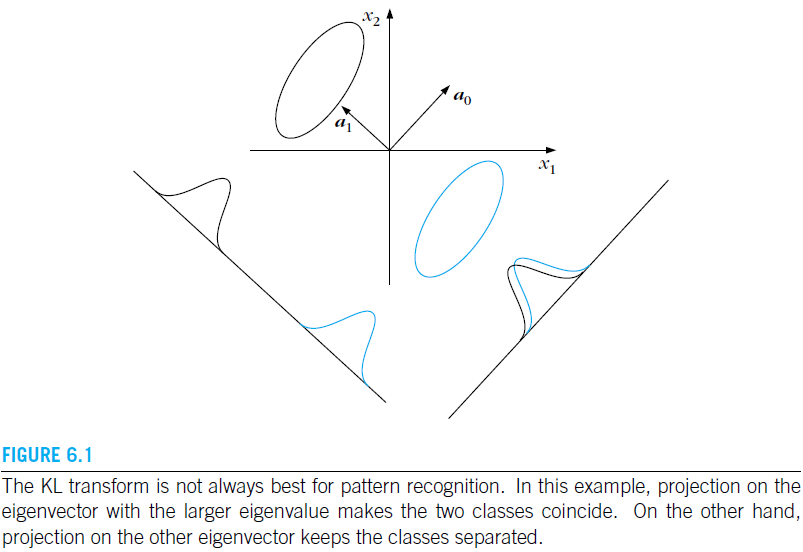
Nonlinear-Kernel PCA (6.7.1)

As its name suggests, this is a kernelized version of the classical PCA. Given the data set $\mathbf{X}$, we make an implicit mapping into a reproducing kernel Hilbert space $H$,
$$\mathbf{x}\in \mathbf{X}\mapsto \mathbf{\varphi }(\mathbf{x})\in H$$
Let ${\mathbf{x}}_i,i=1,2.\cdots ,n$, be the available training points. We will work with an estimate of the correlation matrix in $H$ obtained as an average over the known sample points
$$\mathbf{R}=\frac{1}{n}\sum _{i=1}^n\mathbf{\varphi }({\mathbf{x}}_i)\mathbf{\varphi }({\mathbf{x}}_i{)}^T\text{\hspace{1em}(KPCA.1)}$$
As in PCA, performing the eigendecomposition of $\mathbf{R}$, that is
$$\mathbf{R}\mathbf{v}=\lambda \mathbf{v}\text{\hspace{1em}(KPCA.2)}$$
By the definition of $\mathbf{R}$, it can be shown that $\mathbf{v}$ lies in the span of { ϕ ( x 1 ) , ϕ ( x 2 ) , ⋯   , ϕ ( x n ) } { boldsymbol phi(mathbf x_1), boldsymbol phi(mathbf x_2),cdots, boldsymbol phi(mathbf x_n)} {ϕ(x1​),ϕ(x2​),⋯,ϕ(xn​)}. Indeed,
$$\lambda \mathbf{v}=\left(\frac{1}{n}\sum _{i=1}^n\mathbf{\varphi }({\mathbf{x}}_i)\mathbf{\varphi }({\mathbf{x}}_i{)}^T\right)\mathbf{v}=\frac{1}{n}\sum _{i=1}^n\left(\mathbf{\varphi }({\mathbf{x}}_i{)}^T\mathbf{v}\right)\mathbf{\varphi }({\mathbf{x}}_i)$$
and for $\lambda \ne 0$ we can write
$$\mathbf{v}=\sum _{i=1}^{n}a(i)\mathbf{\varphi }({\mathbf{x}}_i)\text{\hspace{1em}(KPCA.3)}$$
Denote
$$\mathcal{K}(i,j)=K({\mathbf{x}}_i,{\mathbf{x}}_j)=\mathbf{\varphi }({\mathbf{x}}_i{)}^T\mathbf{\varphi }({\mathbf{x}}_j)\text{\hspace{1em}(KPCA.4)}$$
where $K(\cdot ,\cdot )$ being the adopted kernel function, and $\mathcal{K}$ is the Gram matrix.

From $(KPCA.1),(KPCA.2)$ and $(KPCA.3)$, we have
$$\frac{1}{n}[\mathbf{\varphi }({\mathbf{x}}_1)\cdots \mathbf{\varphi }({\mathbf{x}}_n)]\left[\begin{array}{c}\mathbf{\varphi }({\mathbf{x}}_1{)}^T\\ ⋮\\ \mathbf{\varphi }({\mathbf{x}}_n{)}^T\end{array}\right][\mathbf{\varphi }({\mathbf{x}}_1)\cdots \mathbf{\varphi }({\mathbf{x}}_n)]\mathbf{a}=\lambda [\mathbf{\varphi }({\mathbf{x}}_1)\cdots \mathbf{\varphi }({\mathbf{x}}_n)]\mathbf{a}$$
which can be satisfied if
$$\mathcal{K}\mathbf{a}=n\lambda \mathbf{a}\text{\hspace{1em}(KPCA.5)}$$
Thus, the $k$-th eigenvector of $\mathbf{R}$, corresponding to the $k$-th (nonzero) eigenvector of $\mathcal{K}$ is expressed as
$${\mathbf{v}}_k=\sum _{i=1}^n{a}_k(i)\mathbf{\varphi }\left({\mathbf{x}}_i\right),k=1,2,\dots ,p\text{\hspace{1em}(KPCA.6)}$$
where ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_p$ denote the respective eigenvalues in descending order and ${\lambda }_p$ is the smallest nonzero one and ${\mathbf{a}}_k^T\equiv \left[a_k(1),\dots ,a_k(n)\right]$ is the $k$-th eigenvector of the Gram matrix. The latter is assumed to be normalized so that $⟨{\mathbf{v}}_k,{\mathbf{v}}_k⟩=1,k=1,2,\dots ,p,$ where $⟨\cdot ,\cdot ⟩$ is the dot product in the Hilbert space $H.$ This imposes an equivalent normalization on the respective ${\mathbf{a}}_k$ 's, resulting from
$$\begin{array}{rl}1=⟨{\mathbf{v}}_k,{\mathbf{v}}_k⟩& =⟨\sum _{i=1}^n{\mathbf{a}}_k(i)\mathbf{\varphi }\left(x_i\right),\sum _{j=1}^n{\mathbf{a}}_k(j)\mathbf{\varphi }\left(x_j\right)⟩\\ & =\sum _{i=1}^n\sum _{j=1}^n{\mathbf{a}}_k(i){\mathbf{a}}_k(j)\mathcal{K}(i,j)\\ & ={\mathbf{a}}_k^T\mathcal{K}{\mathbf{a}}_k=n{\lambda }_k{\mathbf{a}}_k^T{\mathbf{a}}_k,k=1,2,\dots ,p\end{array}\text{\hspace{1em}(KPCA.7)}$$
We are now ready to summarize the basic steps for performing a kernel PCA. Given a vector $\mathbf{x}\in {\mathcal{R}}^N$ and a kernel function $K(\cdot ,\cdot )$:

• Compute the Gram matrix $\mathcal{K}(i,j)=K\left({\mathbf{x}}_i,{\mathbf{x}}_j\right),i,j=1,2,\dots ,n$
• Compute the $m$ dominant eigenvalues/eigenvectors ${\lambda }_k,{\mathbf{a}}_k,k=1,2,\dots ,m$ of $\mathcal{K}$ (Eq.$(KPCA.5)$).
• Perform the required normalization (Eq. $(KPCA.7)$).
• Compute the $m$ projections onto each one of the dominant eigenvectors,

$$\mathbf{y}(k)\equiv ⟨{\mathbf{v}}_k,\mathbf{\varphi }(\mathbf{x})⟩=\sum _{i=1}^n{\mathbf{a}}_k(i)K\left({\mathbf{x}}_i,\mathbf{x}\right),k=1,2,\dots ,m\text{\hspace{1em}(KPCA.8)}$$

The operations given in $(KPCA.8)$ correspond to a nonlinear mapping in the input space. Note that, in contrast to the linear PCA, the dominant eigenvectors $v_k,k=1,2,\dots ,m$, are not computed explicitly.

最后

以上就是鳗鱼小懒猪为你收集整理的Feature Selection and Extraction的全部内容，希望文章能够帮你解决Feature Selection and Extraction所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。