本文是 2020人工神经网络第一次作业 的参考答案第四部分
➤04 第四题参考答案
1.使用BP网络逼近Hermit函数
f
(
x
)
=
1.1
(
1
−
x
+
2
x
2
)
⋅
e
−
x
2
2
fleft( x right) = 1.1left( {1 - x + 2x^2 } right) cdot e^{ - {{x^2 } over 2}}
f(x)=1.1(1−x+2x2)⋅e−2x2
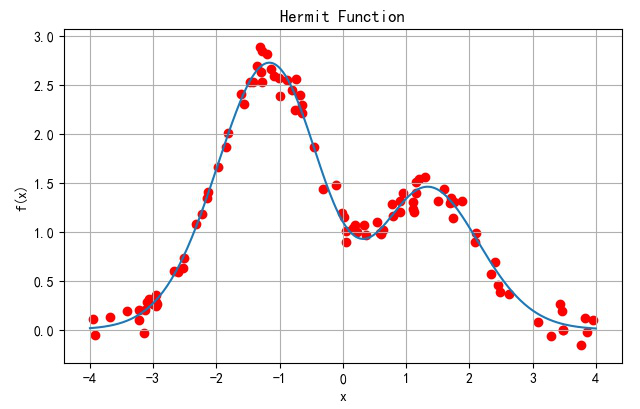
▲ Hermit函数 以及相关函数随机采集数据（红色)
1
2
3
4
5
6
7
8
9def Hermit(x): return 1.1 * (1 - x + 2 * x * x) * exp(-x**2/2) x = linspace(-4, 4, 250) fx = Hermit(x) sx = random.uniform(-4, 4, 100) fs = Hermit(sx) + random.normal(0, 0.1, len(sx))
(1) 隐层节点：10
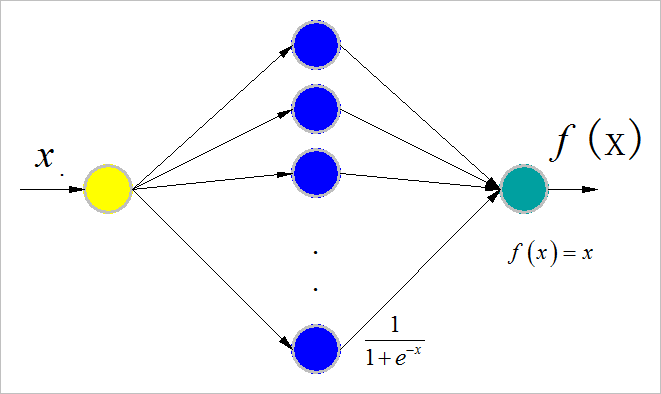
▲ 网络结构
上述BP网络实现程序参见后附录中的：1.BP网络函数逼近程序
训练超参数：
- 学习速率：
η
=
0.5
eta = 0.5
η=0.5
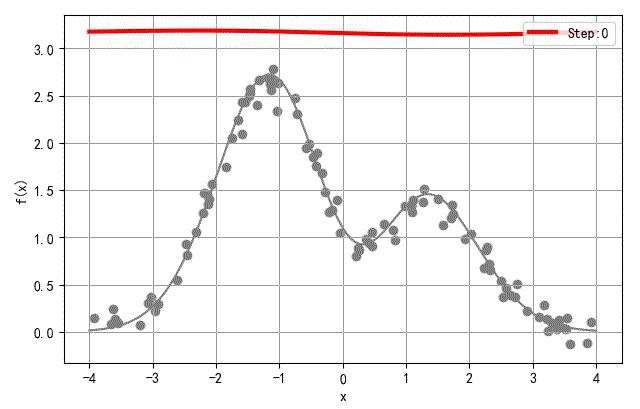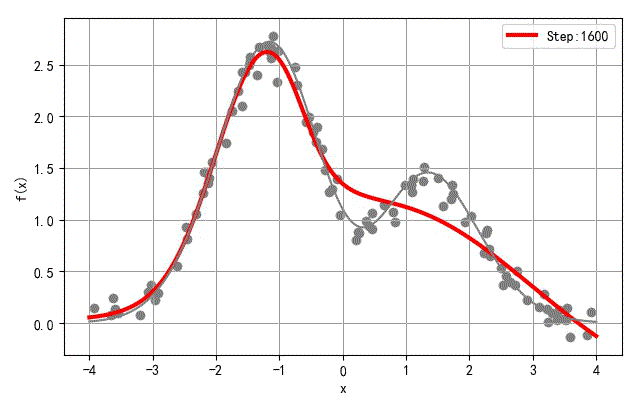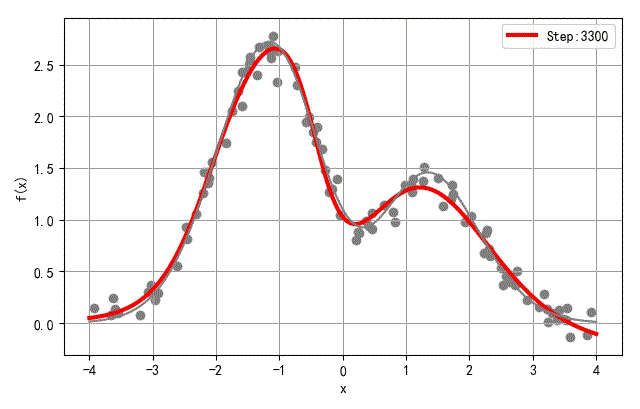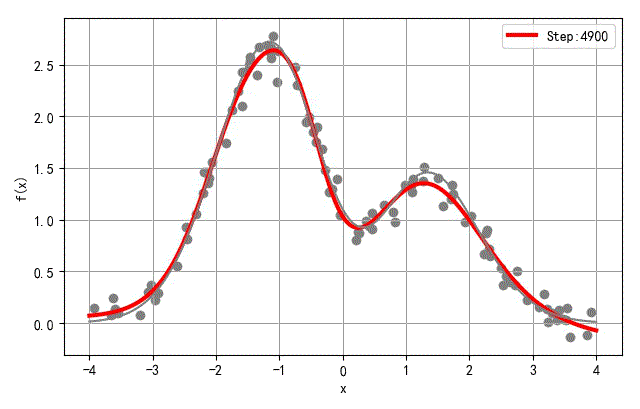
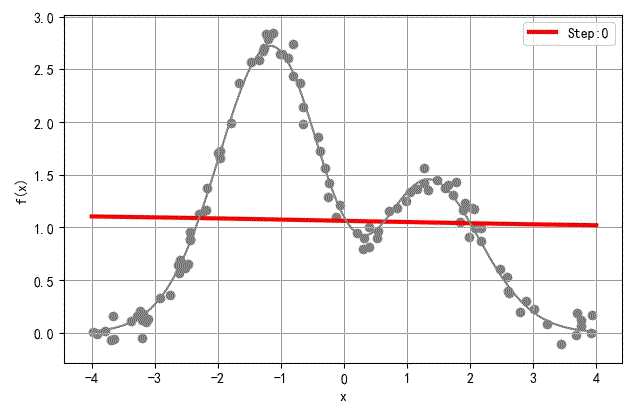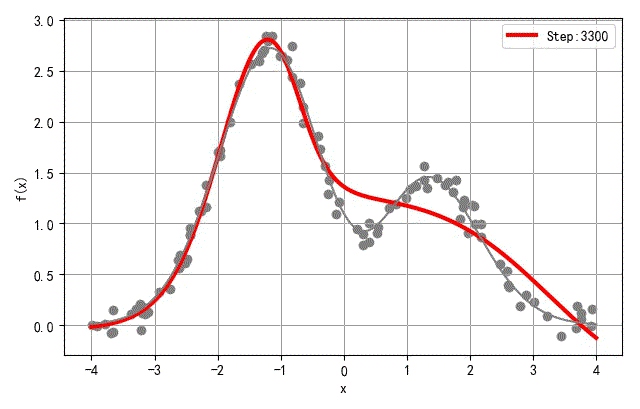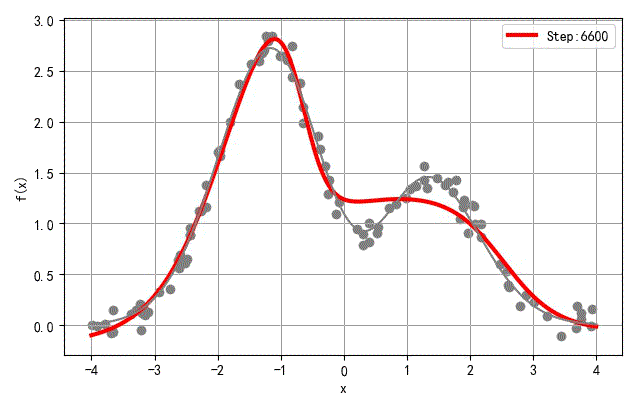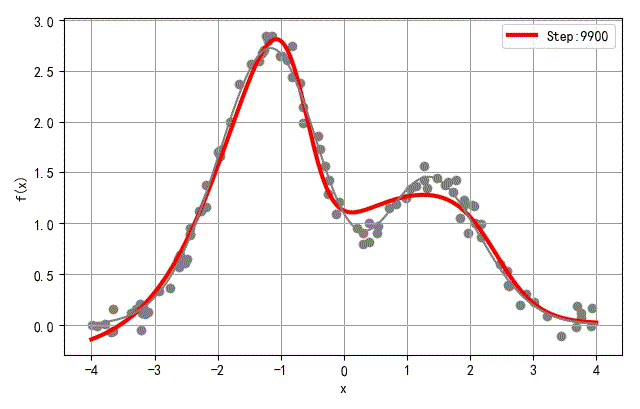
▲ 收敛过程中网络输出输入之间函数变化过程
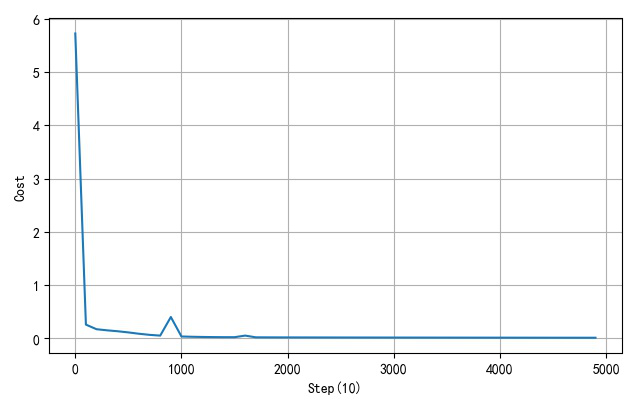
▲ 网络训练误差收敛曲线
(2) 不同隐层节点个数
- 隐层三个节点：
▲ 隐层三个节点训练过程
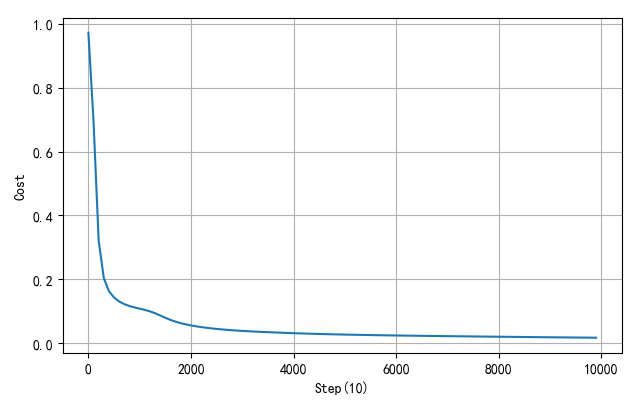
▲ 隐层三个节点网络误差收敛曲线
- 隐层节点数量：20
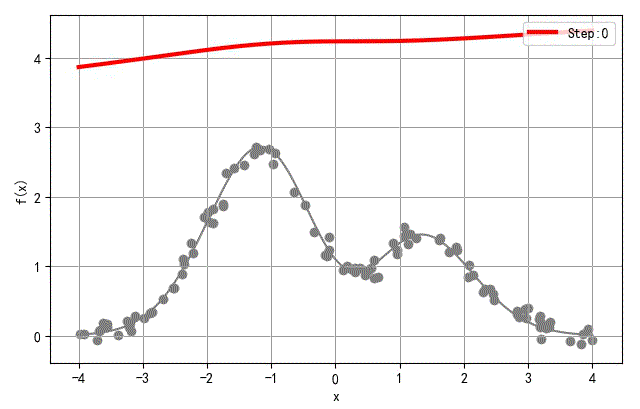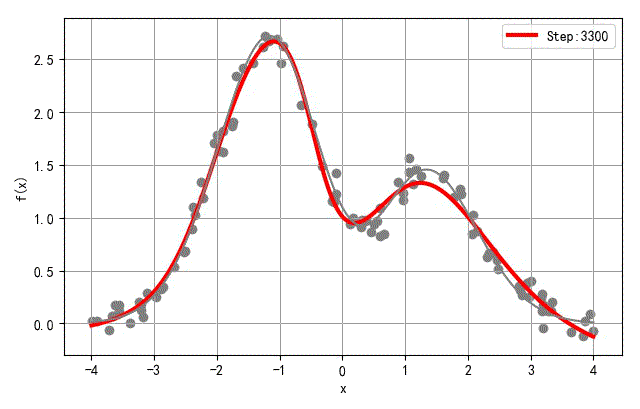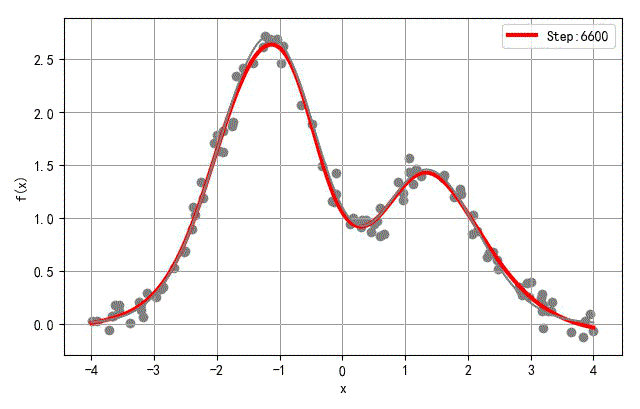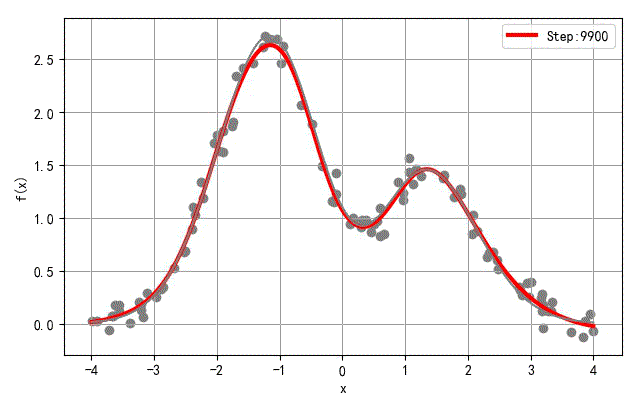
▲ 隐层20个节点网络训练过程
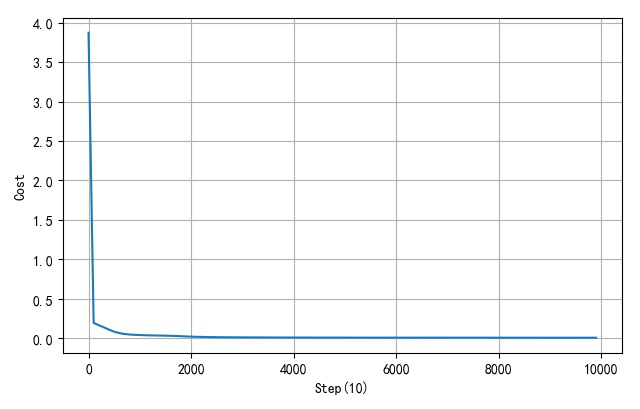
▲ 隐层20个节点网络误差收敛过程
(3) 不同隐层节点数目与网络误差
构造不同隐层节点数量（2,3，…,10）,使用学习速率0.5， 训练10000循环，对应的网络收敛后的不同的误差。
| 隐层节点个数 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| 网络逼近误差 | 0.1122 | 0.0202 | 0.00927 | 0.0102 | 0.01016 | 0.00704 | 0.01017 | 0.006515 | 0.009511 |
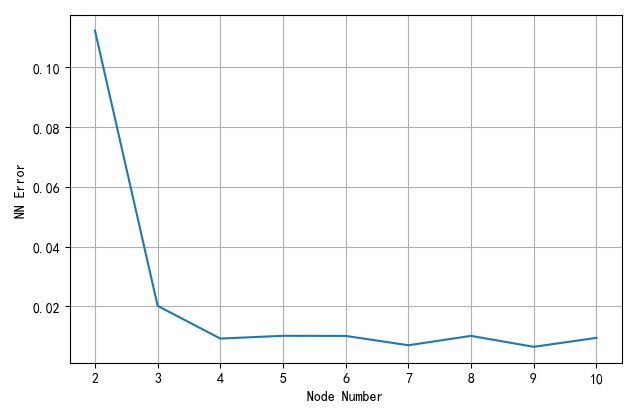
▲ 不同的隐层节点对应网络逼近误差
从上面训练结果可以看到，当隐层节点大于等4之后，网络对于Hermit函数逼近的精度就降低到0.01之下了。
2.使用RBF网络进行函数逼近
(1) 训练样本
样本数取32个。在[-4,4]之间均匀分布，同样添加标准差为0.1的正态分布噪声。下面红色点为加有噪声之后的训练样本。
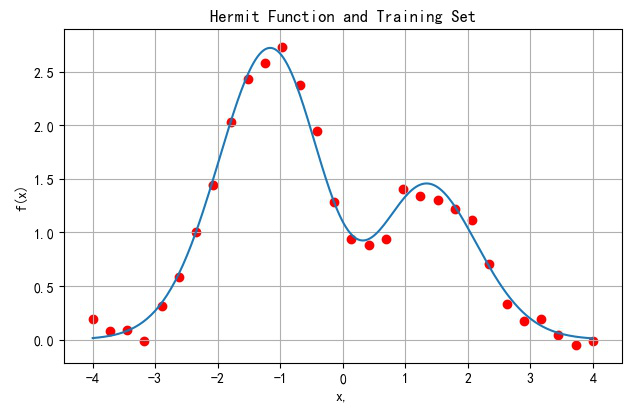
▲ Hermit函数以及均匀采样的32个样本
1
2
3
4
5
6
7
8def Hermit(x): return 1.1 * (1 - x + 2 * x * x) * exp(-x**2/2) x_line = linspace(-4, 4, 250) y_line = Hermit(x_line) x_train = linspace(-4, 4, 30) y_train = Hermit(x_train) + random.normal(0, 0.1, len(x_train))
(2) 网络结构
构建RBF网络，选择RBF网络隐层节点的个数 N h ∈ ( 3 , 30 ) N_h in left( {3,,,,30} right) Nh∈(3,30)。隐层节点的径向基函数采用高斯函数形式的函数：
f ( x ) = e − ∣ x − x c ∣ 2 2 σ 2 fleft( x right) = e^{ - {{left| {x - x_c } right|^2 } over {2sigma ^2 }}} f(x)=e−2σ2∣x−xc∣2
每个隐层神经元的参数包括：中心 x c x_c xc，方差： σ sigma σ。
RBF网络Python实现程序参见后面附录中的：2.RBF网络实现程序
(3) 网络训练
由于训练样本是在（-4,4）之间的均匀采样，所以构造隐层节点的中心 x c x_c xc位置也在（-4,4）之间均匀采样。隐层节点的方差取隐层节点中心平均距离： σ = 8 N h sigma = {8 over {N_h }} σ=Nh8。
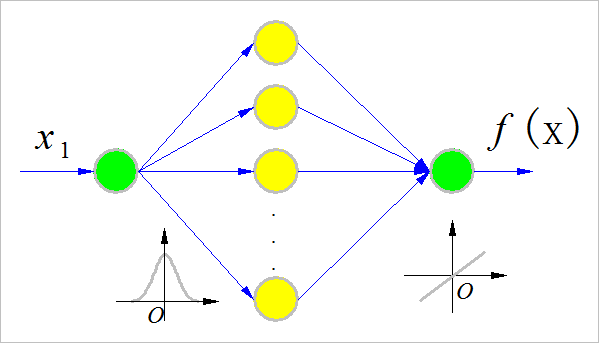
▲ RBF网络结构
在这里，选取网络隐层节点个数： N h = 10 N_h = 10 Nh=10。
隐层各节点的中心位置：
| Node#10 | -4.00 | -3.11 | -2.22 | -1.33 | -0.44 | 0.44 | 1.33 | 2.22 | 3.11 | 4.00 |
|---|
根据训练样本 { x i , y i } i = 1 , ⋯ , 30 left{ {x_i ,y_i } right}_{i = 1, cdots ,30} {xi,yi}i=1,⋯,30，计算出隐层对应的输出矩阵： H 30 = { h 1 , h 2 , ⋯ , h 30 } H_{30} = left{ {h_1 ,h_2 , cdots ,h_{30} } right} H30={h1,h2,⋯,h30}，其中每个 h i h_i hi都对应着某一个样本 x i x_i xi输入之后得到的隐层输出。
RBF网络输出为： y ^ i = W T ⋅ h i hat y_i = W^T cdot h_i y^i=WT⋅hi
其中 W W W是隐层到网络试试部分的链接权系数。
将样本的期望输出组成向量： y ˉ = { y 1 , y 2 , ⋯ , y 30 } T bar y = left{ {y_1 ,y_2 , cdots ,y_{30} } right}^T yˉ={y1,y2,⋯,y30}T
对于隐层到输出节点的加权系数 W W W，可以直接通过求取伪逆的方式获得：
W T = y ˉ ⋅ ( H 30 T ⋅ H 30 + λ ⋅ I 30 ) − 1 ⋅ H 30 T W^T = bar y cdot left( {H_{30}^T cdot H_{30} + lambda cdot I_{30} } right)^{ - 1} cdot H_{30}^T WT=yˉ⋅(H30T⋅H30+λ⋅I30)−1⋅H30T
其中 λ ⋅ I 30 lambda cdot I_{30} λ⋅I30加入放置矩阵求逆出现奇异设定的。 λ lambda λ可以选取一个比较小的数值，比如0.0001。
(4) 训练结果
通过上方法得到RBF网络参数：隐层节点的径向基函数的中心点，方差，隐层到输出层的加权系数，RBF网络便设计完成了。
下面是网络构建之后，实际对应的函数关系。对于训练样本数据，网络的误差为： V a r ( [ y ^ i − y i ] i = 1 , 2 , ⋯ , 30 ) = 0.00569 Varleft( {left[ {hat y_i - y_i } right]_{i = 1,2, cdots ,30} } right) = 0.00569 Var([y^i−yi]i=1,2,⋯,30)=0.00569
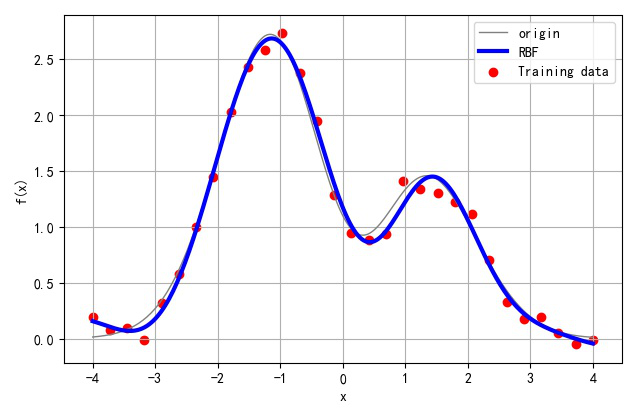
▲ 隐层节点为10 的情况下RBF网络函数拟合的结果
(5) 不同隐层节点对应训练误差
选取网络中间隐层节点的个数 N h N_h Nh从3变化到30，对应网络训练结果如下。
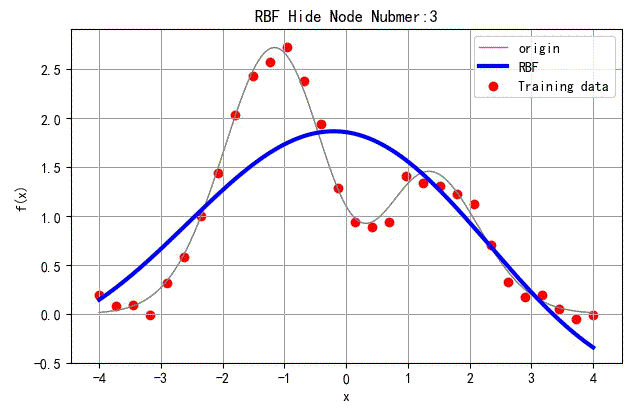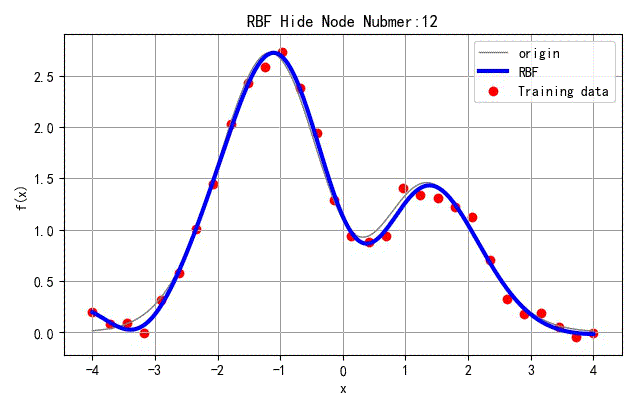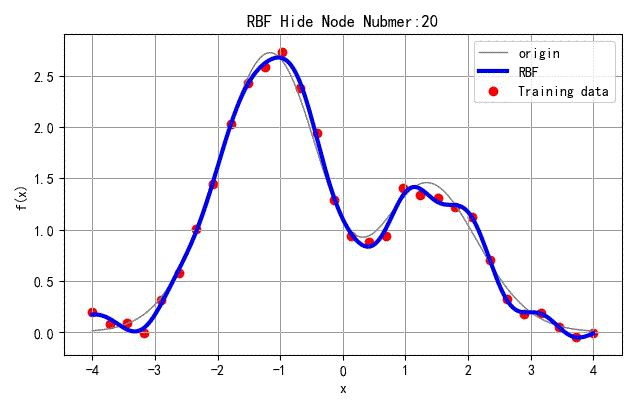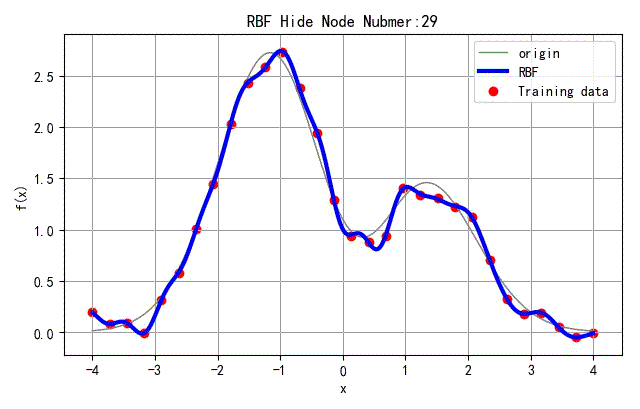
▲ 不同隐层节点数量对应网络结果
随着RBF网络隐层节点个数从3变化到30，对应的网络训练误差的变化曲线如下：
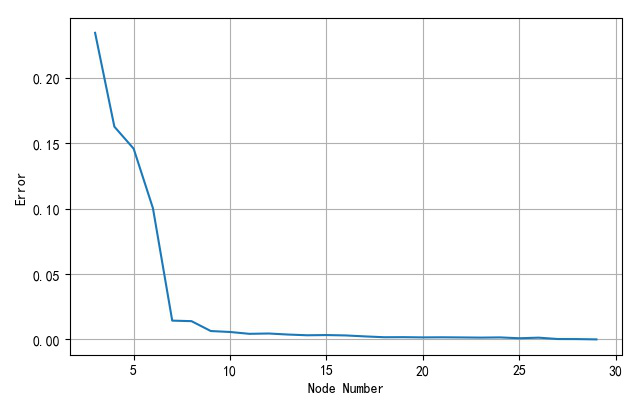
▲ 不同网络隐层节点个数对应网络训练误差
可以看到其中当网络节点大于8之后，网络训练误差就变得非常小了。
(6) 隐层节点的方差对于函数逼近的影响
为了展示RBF隐层节点的方差参数对于网络设计的影响，下面去网络隐层节点的方法从0.001变化的4的过程中，对应网络训练误差的影响。
在下面的例子中，选取隐层节点的个数
N
h
=
8
N_h = 8
Nh=8。
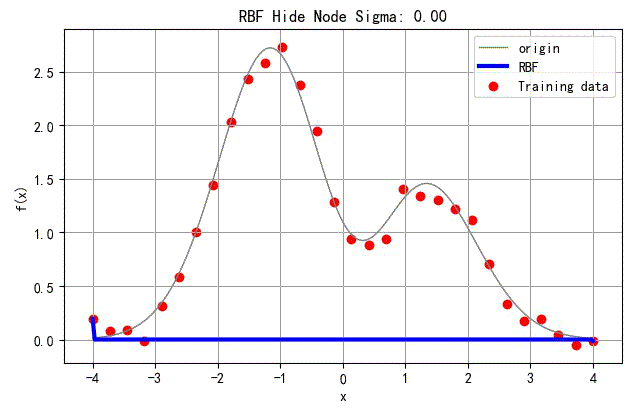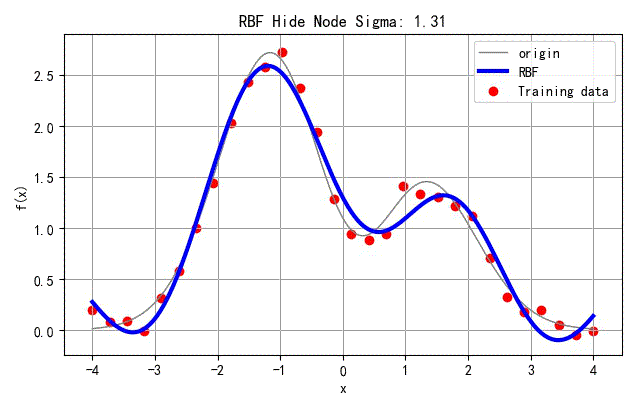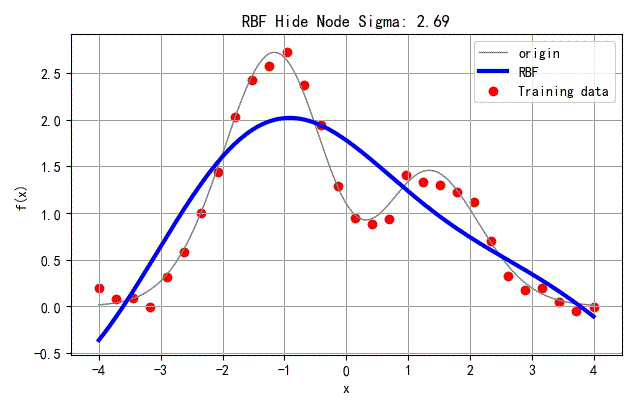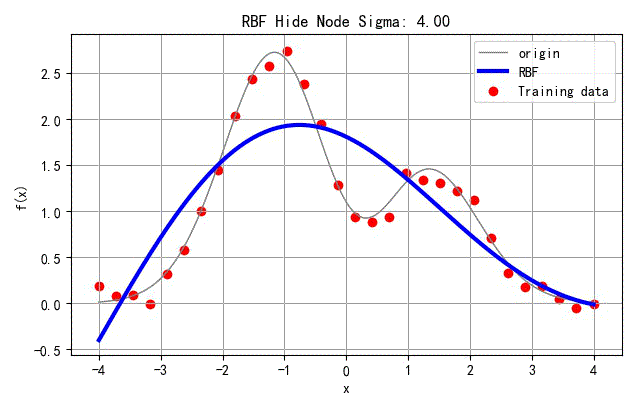
▲ 不同隐层节点方差对应的网络训练结果
下面显示了网络训练误差随着隐层节点方差的变化的情况。可以看出当方差在
σ
=
8
N
h
=
8
8
=
1
sigma = {8 over {N_h }} = {8 over 8} = 1
σ=Nh8=88=1附近是，对应的网络训练方差接近最小。
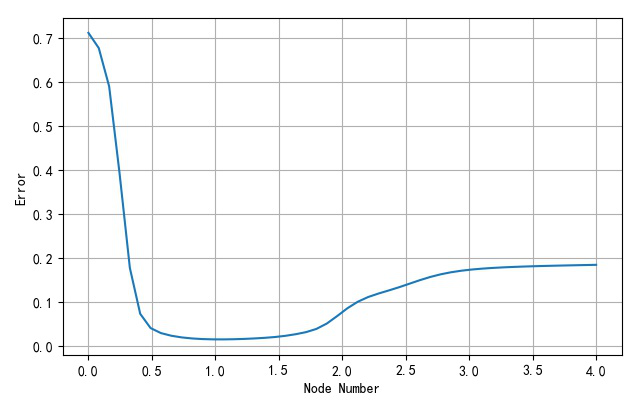
▲ 不同隐层节点方差对应网络训练误差曲线
➤※ 作业1-4中的程序
1.BP网络函数逼近程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204#!/usr/local/bin/python # -*- coding: gbk -*- #============================================================ # HW14BP.PY -- by Dr. ZhuoQing 2020-11-17 # # Note: #============================================================ from headm import * #------------------------------------------------------------ # Samples data construction random.seed(int(time.time())) #------------------------------------------------------------ def Hermit(x): return 1.1 * (1 - x + 2 * x * x) * exp(-x**2/2) x_data = random.uniform(-4, 4, 100) y_data = Hermit(x_data) + random.normal(0, 0.1, len(x_data)) x_data = x_data.reshape(-1, 1) y_data = y_data.reshape(1, -1) xx = linspace(-4, 4, 250) yy = Hermit(xx) #------------------------------------------------------------ def shuffledata(X, Y): id = list(range(X.shape[0])) random.shuffle(id) return X[id], (Y.T[id]).T #------------------------------------------------------------ # Define and initialization NN def initialize_parameters(n_x, n_h, n_y): W1 = random.randn(n_h, n_x) * 0.5 # dot(W1,X.T) W2 = random.randn(n_y, n_h) * 0.5 # dot(W2,Z1) b1 = zeros((n_h, 1)) # Column vector b2 = zeros((n_y, 1)) # Column vector parameters = {'W1':W1, 'b1':b1, 'W2':W2, 'b2':b2} return parameters #------------------------------------------------------------ # Forward propagattion # X:row->sample; # Z2:col->sample def forward_propagate(X, parameters): W1 = parameters['W1'] b1 = parameters['b1'] W2 = parameters['W2'] b2 = parameters['b2'] Z1 = dot(W1, X.T) + b1 # X:row-->sample; Z1:col-->sample A1 = 1/(1+exp(-Z1)) # A1 = (1-exp(-Z1))/(1+exp(-Z1)) Z2 = dot(W2, A1) + b2 # Z2:col-->sample A2 = Z2 # Linear output cache = {'Z1':Z1, 'A1':A1, 'Z2':Z2, 'A2':A2} return Z2, cache #------------------------------------------------------------ # Calculate the cost # A2,Y: col->sample def calculate_cost(A2, Y, parameters): err = [x1-x2 for x1,x2 in zip(A2.T, Y.T)] cost = [dot(e,e) for e in err] return mean(cost) #------------------------------------------------------------ # Backward propagattion def backward_propagate(parameters, cache, X, Y): m = X.shape[0] # Number of the samples W1 = parameters['W1'] W2 = parameters['W2'] A1 = cache['A1'] A2 = cache['A2'] dZ2 = (A2 - Y) dW2 = dot(dZ2, A1.T) / m db2 = sum(dZ2, axis=1, keepdims=True) / m dZ1 = dot(W2.T, dZ2) * (A1 * (1-A1)) # dZ1 = dot(W2.T, dZ2) * (1-A1**2) dW1 = dot(dZ1, X) / m db1 = sum(dZ1, axis=1, keepdims=True) / m grads = {'dW1':dW1, 'db1':db1, 'dW2':dW2, 'db2':db2} return grads #------------------------------------------------------------ # Update the parameters def update_parameters(parameters, grads, learning_rate): W1 = parameters['W1'] b1 = parameters['b1'] W2 = parameters['W2'] b2 = parameters['b2'] dW1 = grads['dW1'] db1 = grads['db1'] dW2 = grads['dW2'] db2 = grads['db2'] W1 = W1 - learning_rate * dW1 W2 = W2 - learning_rate * dW2 b1 = b1 - learning_rate * db1 b2 = b2 - learning_rate * db2 parameters = {'W1':W1, 'b1':b1, 'W2':W2, 'b2':b2} return parameters #------------------------------------------------------------ # Define the training DISP_STEP = 100 #------------------------------------------------------------ pltgif = PlotGIF() #------------------------------------------------------------ def train(X, Y, num_iterations, learning_rate, print_cost=False): n_x = 1 n_y = 1 n_h = 10 lr = learning_rate parameters = initialize_parameters(n_x, n_h, n_y) XX,YY = shuffledata(X, Y) costdim = [] x = linspace(-4, 4, 250).reshape(-1,1) for i in range(0, num_iterations): A2, cache = forward_propagate(XX, parameters) cost = calculate_cost(A2, YY, parameters) grads = backward_propagate(parameters, cache, XX, YY) parameters = update_parameters(parameters, grads, lr) if print_cost and i % DISP_STEP == 0: printf('Cost after iteration:%i: %f'%(i, cost)) costdim.append(cost) plt.clf() y,cache = forward_propagate(x, parameters) plt.plot(x.reshape(-1,1), y.reshape(-1,1), linewidth=3, color='r', label='Step:%d'%i) plt.plot(xx, yy, color='gray') plt.scatter(XX, YY, color='gray') plt.xlabel("x") plt.ylabel("f(x)") plt.grid(True) plt.tight_layout() plt.legend(loc='upper right') plt.draw() plt.pause(.1) pltgif.append(plt) if cost < 0.0001: break XX,YY = shuffledata(X, Y) return parameters, costdim #------------------------------------------------------------ parameter,costdim = train(x_data, y_data, 10000, 0.5, True) pltgif.save(r'd:temp1.gif') printf('cost:%f'%costdim[-1]) #------------------------------------------------------------ plt.clf() plt.plot(arange(len(costdim))*DISP_STEP, costdim) plt.xlabel("Step(10)") plt.ylabel("Cost") plt.grid(True) plt.tight_layout() plt.show() #------------------------------------------------------------ # END OF FILE : HW14BP.PY #============================================================
2.RBF网络实现程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112#!/usr/local/bin/python # -*- coding: gbk -*- #============================================================ # HM14RBF.PY -- by Dr. ZhuoQing 2020-11-19 # # Note: #============================================================ from headm import * #------------------------------------------------------------ random.seed(3) #------------------------------------------------------------ def Hermit(x): return 1.1 * (1 - x + 2 * x * x) * exp(-x**2/2) x_line = linspace(-4, 4, 250) y_line = Hermit(x_line) RBF_SAMPLE_NUMBER = 30 x_train = linspace(-4, 4, RBF_SAMPLE_NUMBER) y_train = Hermit(x_train) + random.normal(0, 0.1, len(x_train)) ''' plt.plot(x_line, y_line) plt.scatter(x_train, y_train, color='r') plt.xlabel("x,") plt.ylabel("f(x)") plt.title('Hermit Function and Training Set') plt.grid(True) plt.tight_layout() plt.show() ''' #------------------------------------------------------------ # calculate the rbf hide layer output # x: Input vector: # H: Hide node : row->sample # sigma: variance of RBF def rbf_hide_out(x, H, sigma): Hx = H - x Hxx = [exp(-dot(e,e)/(sigma**2*2)) for e in Hx] return Hxx def rbf(x, H, sigma, W): Hx = H - x Hxx = array([exp(-dot(e,e)/(sigma**2*2)) for e in Hx]).reshape(-1, 1) return (dot(W.T, Hxx)) #------------------------------------------------------------ y_train = y_train.reshape(1, -1) def rbf_train_sim(node=10,sigma=1): RBF_HIDE_NODE = node RBF_HIDE_SIGMA = sigma Hnode = linspace(-4, 4, RBF_HIDE_NODE).reshape(-1,1) # row-->sample Hout = array([rbf_hide_out(x, Hnode, RBF_HIDE_SIGMA) for x in x_train]).T W = dot(y_train, dot(linalg.inv(eye(RBF_SAMPLE_NUMBER)*0.0001+dot(Hout.T,Hout)),Hout.T)).T yout = dot(W.T, Hout) err = yout - y_train error = var(err) return W, Hnode, error #------------------------------------------------------------ err_dim = [] node_dim = [] pltgif = PlotGIF() for s in linspace(0.001, 4, 50): W, Hnode, error = rbf_train_sim(8, s) err_dim.append(error) node_dim.append(s) y_rbf = [rbf(x, Hnode, s, W)[0] for x in x_line] plt.clf() plt.plot(x_line, y_line, linewidth=1, color='gray', label='origin') plt.scatter(x_train, y_train, color='r', label='Training data') plt.plot(x_line, y_rbf, linewidth=3, color='blue', label='RBF') plt.xlabel("x") plt.ylabel("f(x)") plt.grid(True) plt.title('RBF Hide Node Sigma:%5.2f'%s) plt.legend(loc="upper right") plt.tight_layout() # plt.show() plt.draw() plt.pause(0.1) pltgif.append(plt) #------------------------------------------------------------ pltgif.save(r'd:temp1.gif') plt.clf() plt.plot(node_dim, err_dim) plt.xlabel("Node Number") plt.ylabel("Error") plt.grid(True) plt.tight_layout() plt.show() #------------------------------------------------------------ # END OF FILE : HM14RBF.PY #============================================================
最后
以上就是大意咖啡豆最近收集整理的关于2020人工神经网络第一次作业-参考答案第四部分➤04 第四题参考答案➤※ 作业1-4中的程序的全部内容，更多相关2020人工神经网络第一次作业-参考答案第四部分➤04内容请搜索靠谱客的其他文章。
发表评论 取消回复