概述
贝叶斯平滑及其精确解
- 贝叶斯平滑方程
- 贝叶斯最优平滑方程
- Rauch-Tung-Striebel 平滑器
- RTS平滑器
平滑与滤波的区别在于：滤波只是用当前以及之前的量测量去估计当前状态（也可能是未来）的估计值。而贝叶斯平滑在进行估计时还用到了当前时刻之后的量测量。使得估计更加的准确。
贝叶斯平滑方程
贝叶斯平滑的目的在于获得截止到
T
bm{T}
T时刻的量测量后，计算
k
bm{k}
k时刻状态
x
k
bm{x_k}
xk的边缘后验分布，如下：(其中
k
<
T
bm{k<T}
k<T)。
p
(
x
k
∣
y
1
:
T
)
bm{p(x_k|y_{1:T})}
p(xk∣y1:T)
贝叶斯最优平滑方程
对于任意的
k
<
T
bm{k<T}
k<T，计算平滑公式
p
(
x
k
∣
y
1
:
T
)
bm{p(x_k|y_{1:T})}
p(xk∣y1:T) 的后向递归公式（贝叶斯平滑器）可由贝叶斯（固定区间）平滑公式给出：
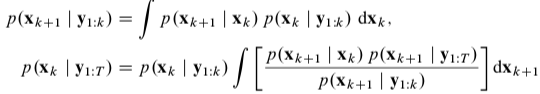其中，
p
(
x
k
∣
y
1
:
k
)
bm{p(x_k|y_{1:k})}
p(xk∣y1:k) 是k时刻的滤波分布。
p
(
x
k
+
1
∣
y
1
:
k
)
bm{p(x_{k+1}|y_{1:k})}
p(xk+1∣y1:k) 是
k
+
1
bm{k+1}
k+1 时刻的预测部分。若是状态中有一部分是离散的，则用求和代替积分。
Rauch-Tung-Striebel 平滑器
RTS平滑器也称为卡尔曼平滑器，可用来计算线性高斯滤波模型的平滑闭型解。
线性高斯模型如下：
x
k
=
A
k
−
1
x
k
−
1
+
q
k
−
1
y
k
=
H
k
x
k
+
r
k
bm{x_k = A_{k-1}x_{k-1}+q_{k-1}} \ bm{y_k = H_kx_k+r_k}
xk=Ak−1xk−1+qk−1yk=Hkxk+rk其闭型解如下：
p
(
x
k
∣
y
1
:
T
)
=
N
(
x
k
∣
m
k
s
,
P
k
s
)
bm{p(x_k|y_{1:T})= N(x_k|m_k^s,P_k^s)}
p(xk∣y1:T)=N(xk∣mks,Pks)这与卡尔曼滤波的区别在于，平滑值是利用了全部量测量
y
1
:
T
bm{y_{1:T}}
y1:T 的估计结果，而滤波值只是利用了
k
bm{k}
k 时刻及其之前所获得的量测量
y
1
:
k
bm{y_{1:k}}
y1:k。
RTS平滑器
（固定区间）RTS平滑器的后向递归方程为：
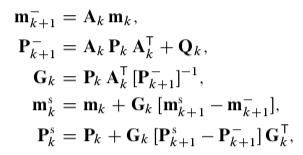其中，
m
k
,
P
k
bm{m_k, P_k}
mk,Pk 是卡尔曼滤波得到的均值和协方差。递归解算从最后一个时刻
T
bm{T}
T 开始，即
m
T
s
=
m
T
，
P
T
s
=
P
T
bm{m_T^s=m_T，P_T^s=P_T}
mTs=mT，PTs=PT。（前两个方程与卡尔曼滤波器的预测方程一致）
最后
以上就是幸福灯泡为你收集整理的贝叶斯平滑及其精确解贝叶斯平滑方程Rauch-Tung-Striebel 平滑器的全部内容，希望文章能够帮你解决贝叶斯平滑及其精确解贝叶斯平滑方程Rauch-Tung-Striebel 平滑器所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复