首先, 从一个BST中删除一个节点可能很tricky。 例如, 对于如下一个BST of integers:
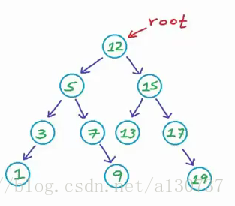
当我们想要删除某个节点的时候, 我们的第一步就是查找到这个元素值所在的位置。 接下来, 我们要保证删除这个节点之后, 我们的二叉搜索树依然是一个二叉搜索树(BST)。 但是这个删除操作本身又是那么的complicated。 因为被删除的项又分为四种情况:
(1): 被删除的节点是叶子节点, 即这个节点既没有左子树, 有没有右子树, 这是最简单的case。
(2): 被删除的节点没有左子树,但是有右子树。 也就是说此节点left成员为NULL。
(3):被删除的节点没有右子树, 但是有左子树。 也就是说此节点right成员为NULL。
(3): 被删除的节点既有左子树, 又有右子树。 这种情况是最复杂的。 要解决这种case, 我们需要将其想法转换为简单的case, 例如(2) 和 (3).
注意(2)和(3)其实是对称的两个cases。
case1: 直接删除也节点, 依然得到BST:
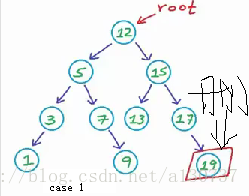
case 2: 删除left 为NULL的节点。 将其parent的link指向此节点的Child, 用temp 指向此节点, 直接delete即可。
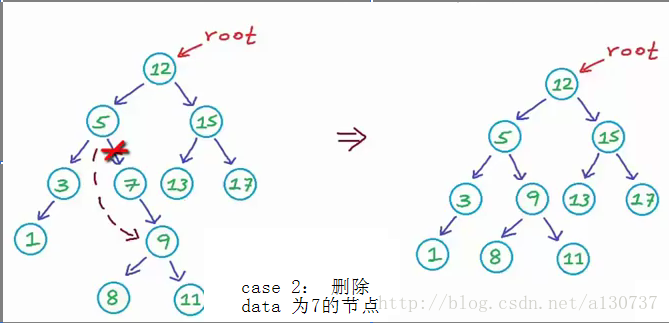
(3) case 3: 同case 2:
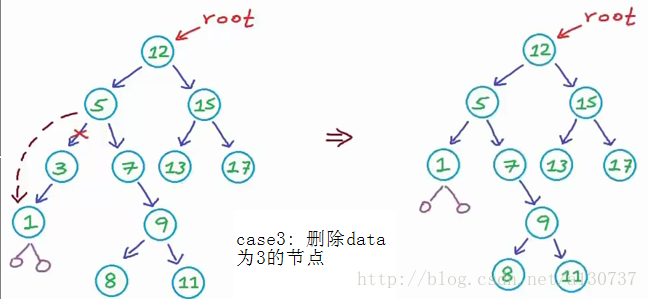
case 4: 删除具有两个孩子的节点。 此时要想保持其实BST, 我们可以将这个节点的左子树的最大的值拷贝到这个节点的data 位置处。 注意由于这个值是左子树的最大的节点的。 所以存储着这个最大值的节点一定没有右孩子。 相当于我们将这个复杂的case, 简化为了case3 的情况了, 接下来删除这个节点就可以了。 删除此类节点当然不会成为上面问题。 另外, 除了这样的一个解决办法外, 我们还可以使用另外的一个办法, 就是将这个复杂的case 转换为case2 , 即找到右子树的最小的值, 此节点没有左孩子。 然后copy到应该删除的节点的位置处, 然后删除这个最小值的节点, 就okay了。
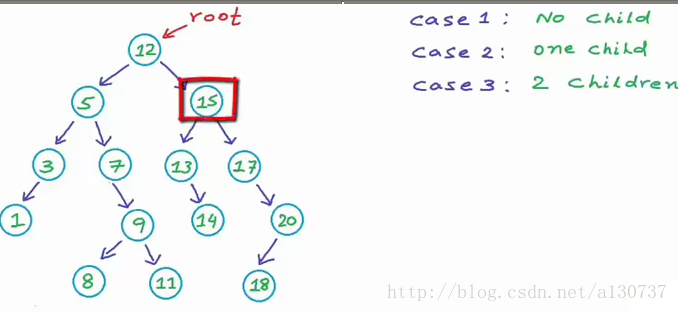
接下来, 找15 的左右子树的最小的节点(或者左子树的最大):
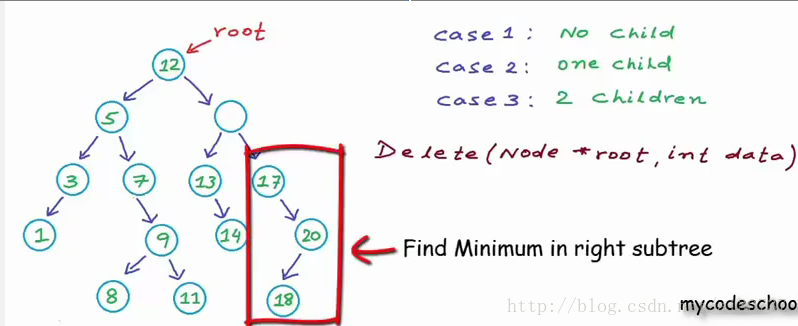
接下来, copy data:
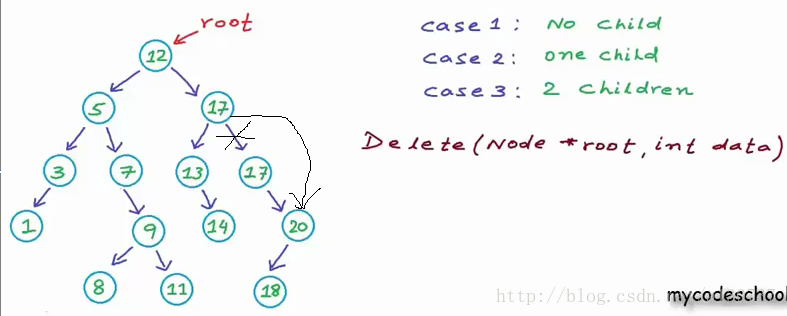
然后删除, 最终得到如下:
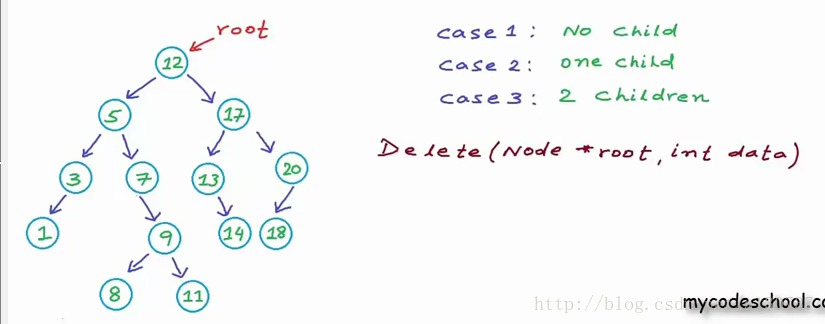
主要C++ 程序如下:
/* Deleting a node from Binary search tree */
#include<iostream>
using namespace std;
struct Node {
int data;
Node *left;
Node *right;
};
//Function to find minimum in a tree.
Node* FindMin(Node* root)
{
while(root->left != NULL) root = root->left;
return root;
}
// Function to search a delete a value from tree.
struct Node* Delete(Node *root, int data) {
if(root == NULL) return root;
else if(data < root->data) root->left = Delete(root->left,data);
else if (data > root->data) root->right = Delete(root->right,data);
// Wohoo... I found you, Get ready to be deleted
else {
// Case 1: No child
if(root->left == NULL && root->right == NULL) {
delete root;
root = NULL;
}
//Case 2: One child
else if(root->left == NULL) {
Node *temp = root;
root = root->right;
delete temp;
}
else if(root->right == NULL) {
struct Node *temp = root;
root = root->left;
delete temp;
}
// case 3: 2 children
else {
Node *temp = FindMin(root->right);
root->data = temp->data;
root->right = Delete(root->right,temp->data);
}
}
return root;
}
//Function to visit nodes in Inorder
void Inorder(Node *root) {
if(root == NULL) return;
Inorder(root->left); //Visit left subtree
cout << root->data << " "; //Print data
Inorder(root->right); // Visit right subtree
}
// Function to Insert Node in a Binary Search Tree
Node* Insert(Node *root,char data) {
if(root == NULL) {
root = new Node();
root->data = data;
root->left = root->right = NULL;
}
else if(data <= root->data)
root->left = Insert(root->left,data);
else
root->right = Insert(root->right,data);
return root;
}
int main() {
/*Code To Test the logic
Creating an example tree
5
/
3 10
/
1 4 11
*/
Node* root = NULL;
root = Insert(root,5); root = Insert(root,10);
root = Insert(root,3); root = Insert(root,4);
root = Insert(root,1); root = Insert(root,11);
cout << "Before delete: ";
Inorder(root);
cout << endl;
// Deleting node with value 5, change this value to test other cases
root = Delete(root,5);
//Print Nodes in Inorder
cout<<"Inorder: ";
Inorder(root);
cout<<"n";
}
运行结果:
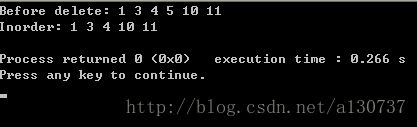
最后
以上就是愉快毛豆最近收集整理的关于C++ delete a node from BST的全部内容,更多相关C++内容请搜索靠谱客的其他文章。








发表评论 取消回复