全概公式
定义:

B是一个事件,则有
证明:
技巧性的问题:
例1
袋中有5个球,其中有3个红球,2个白球,从中每次取出一个球(不放回)用A表示第一次取到红球,B表示第二次取到红球,求
(1)P(A);
(2)P(B)
解
(1)用古典概型n=5,r=3 P(A) = 3/5
(2)直接求P(B)很困难,因为B发生的概率与事件A发生与之有关,用古典概型容易求得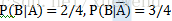
所以可以根据全概率公式求得:
例2
已知男人中有5%是色盲,女人中有1%是色盲,若人群中男女各半。 当在人群中任取一人,问该人是色盲的概率是多少?
逆概公式(贝叶斯公式)
定义:
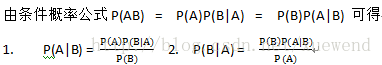
这个就是逆概公式,也叫贝叶斯公式
例1
某地七月份下暴雨的概率为0.7,当下暴雨时,有水灾的概率为0.2;当不下暴雨时,有水灾的概率为0.05,求:
(1)该地七月份有水灾的概率.
(2)当该地七月份已发生水灾时,下暴雨的概率.
理解全概率公式与贝叶斯公式
在全概率公式中,如果将A看成是“结果”,Bi看成是导致结果发生的诸多“原因”之一,那么全概率公式就是一个“原因推结果”的过程。但贝叶斯公式却恰恰相反。贝叶斯公式中,我们是知道结果A已经发生了,所要做的是反过来研究造成结果发生的原因,是XX原因造成的可能性有多大,即“结果推原因”。
基于贝叶斯的定位算法
(http://www.cnblogs.com/LBSer/p/4020370.html )
这一算法google也采用过,上面连接是国内大牛写的一篇文章。
(后面将补充)
最后
以上就是听话泥猴桃最近收集整理的关于概率论—全概公式&逆概公式(贝叶斯公式)的全部内容,更多相关概率论—全概公式&逆概公式(贝叶斯公式)内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。
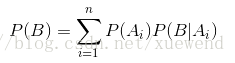


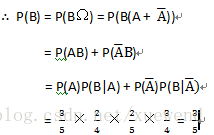










发表评论 取消回复