概述
Overview
2022.5.31开始学习计算机图形学
指导老师推荐使用这套课程 Games101GAMES101-现代计算机图形学入门-闫令琪
对应的教材为“虎书”《Fundamentals Of Computer Graphics》(需要的可扣我
接下来将在CSDN上更新自己的学习笔记
Lectue 1——Overview Of Computer Graphics
1.Self-introduction
为人十分谦逊，自己的研究成果和成就一笔带过
神一般的人物，这里是B站上别人的评论
2.What is computer graphics
The use of computers to synthesize and manipulate virtual information
用电脑去合成和操纵视觉信息
3.Application area
Video Games
Movies
Animations
Design
Virtualization
Augmented Reality
Digital Illustration(数字插画)
Simulation
Graphical User Interfaces
Typography
4.Course Topics
Lecture2——Overview Of Linear Algebra
1.Vectors
Definition
Normaliazation
Addition
Cartesian Coordinate
Multiplication（Dot Product、Cross Product） PS：叉积可以转化为两个矩阵相乘
Orthogonal bases（正交基） and Coordinate frames（坐标系）
2.Matrices
Definition
Multiplication
Transpose
Identity Matrix and Inverse
Lecture3——Transformation（almost Modeling）
1.Definition
（1）Modeling
Translation（平移）
Rotation（旋转）
Scaling（缩放）
（2）Viewing
（3D to 2D）projection（投影）
2. 2D Transformation and Homogeneous Coordinate
本质：左乘一个矩阵即可
Homogeneous Coordinate（齐次坐标）——用来解决Translation问题
（来源：课程配套PPT）
4. simple 3D Tranformation
Lecture 4——Transformation Cont（almost Viewing）
1. 3D Transformation
与2D投影类似
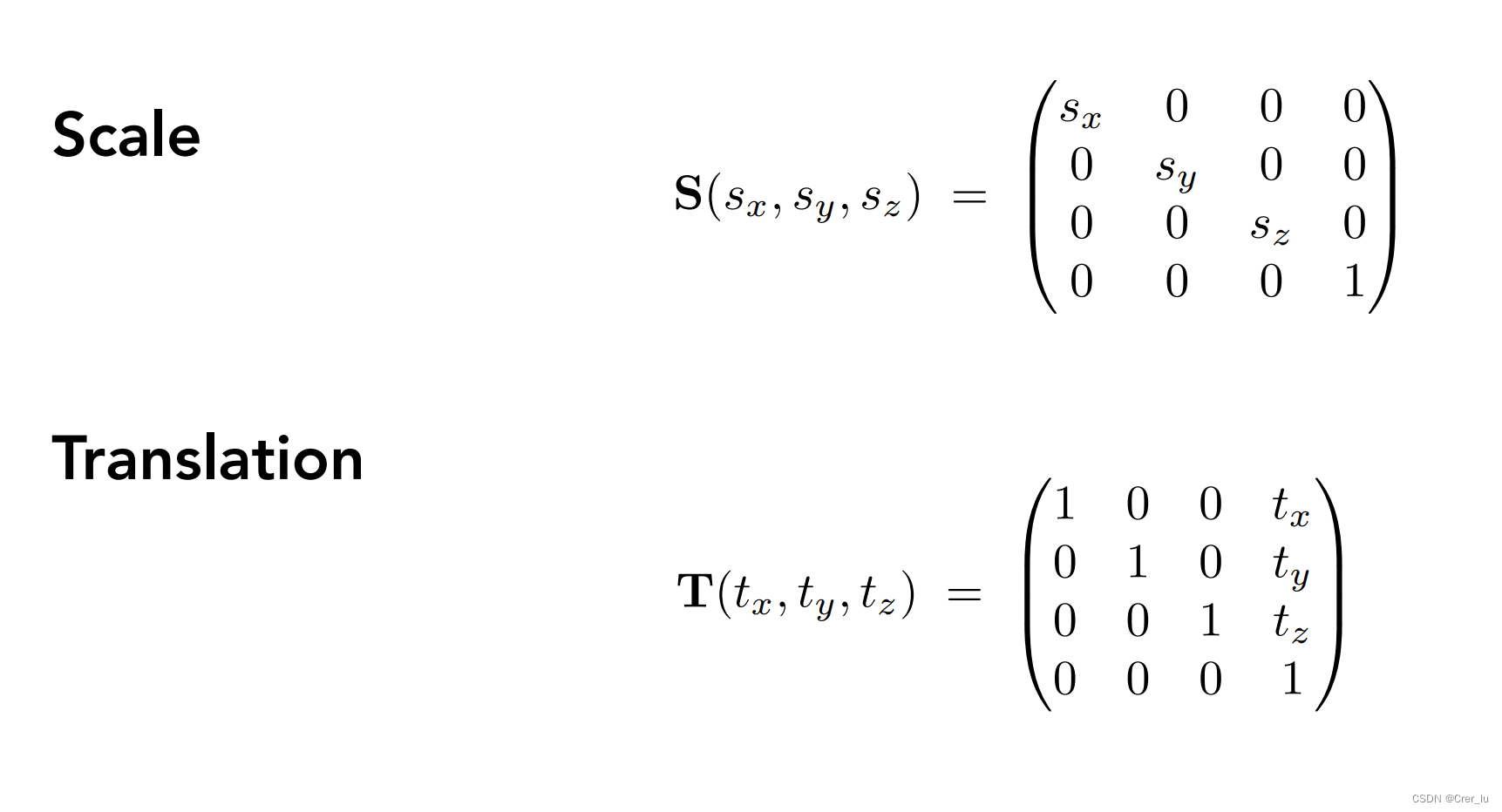
（来源：课程配套PPT）
为什么此处的Ry形式不太一样呢？
是因为右手坐标系下x轴叉乘y轴得到z轴，y轴叉乘z轴得到x轴，而z轴叉乘x轴得到y轴，所以在坐标内显示就有相应体现。
补充知识：Rodrigues‘ Rotation formula
设v是一个三维空间向量，k是旋转轴的单位向量，则v在右手螺旋定则意义下绕旋转轴k旋转角度θ得到的向量可以由三个不共面的向量v, k和k×v构成的标架表示：
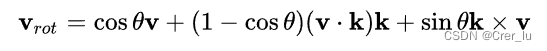
（来源：百度百科）【里面写的推导过程也十分好理解】
2. Viewing
问题引入：想想如何拍照片的？
Modeling（摆姿势）——Viewing（摆相机）——Projection（拍照）
约定俗成：我们统一把观测的位置放在原点，观测方向为-z
怎么样实现呢？——左乘矩阵
M
v
i
e
w
M_{view}
Mview
M
v
i
e
w
M_{view}
Mview包括以下几个部分（图片来源：课程配套PPT）
1.
T
v
i
e
w
T_{view}
Tview
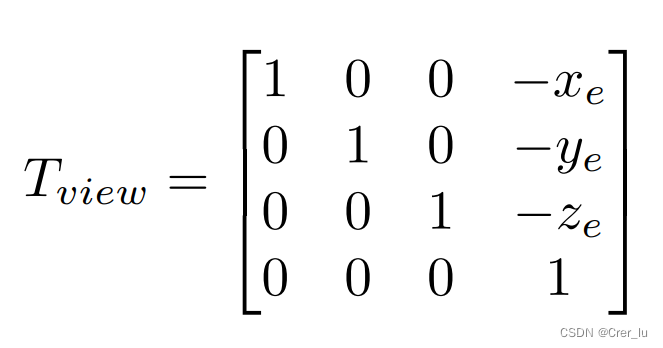
2.
R
v
i
e
w
R_{view}
Rview
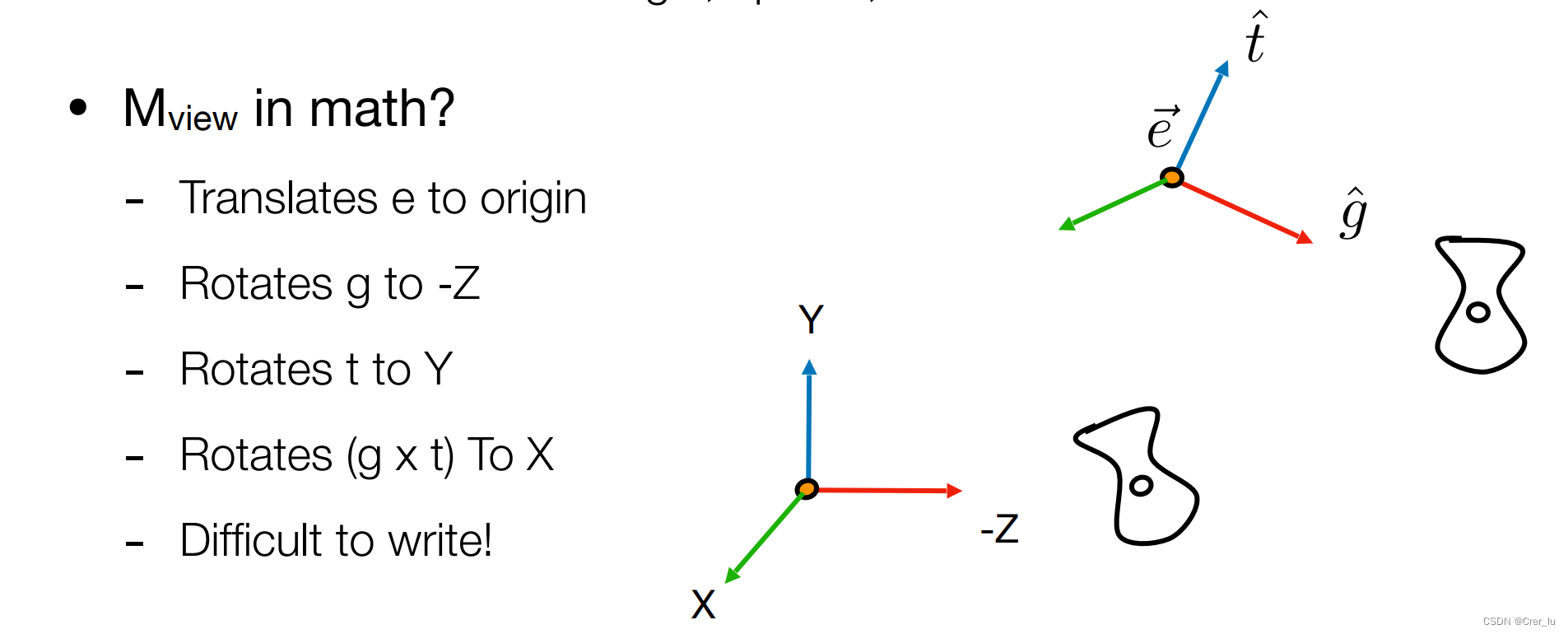
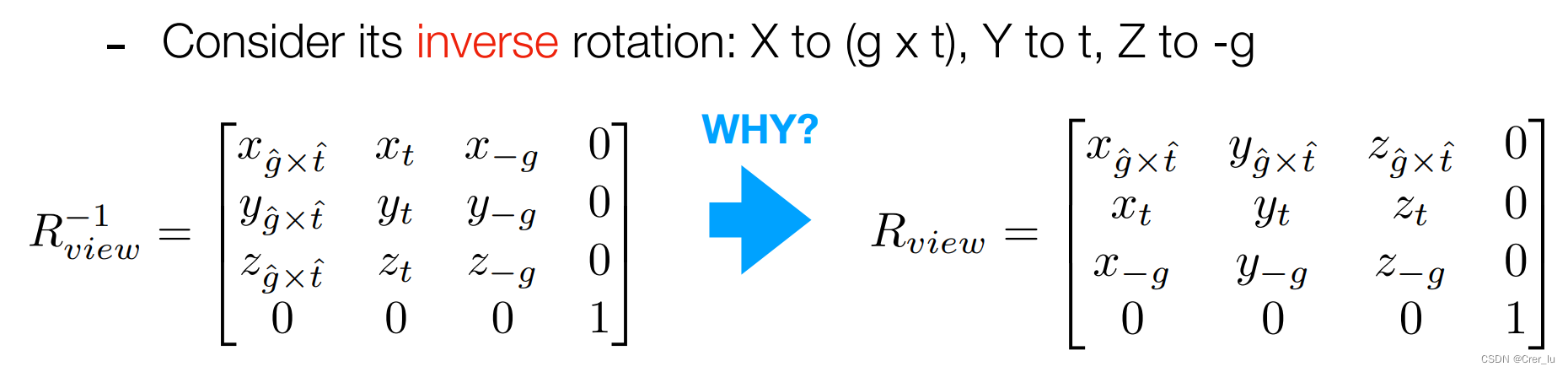
所以我们得到
T
v
i
e
w
=
R
v
i
e
w
⋅
T
v
i
e
w
T_{view}=R_{view}·T_{view}
Tview=Rview⋅Tview
3.Projection
Orthonormal Projection（正交投影）——工图、平行线仍平行
Perspective Projection（透视投影）——实际情况、如同现实生活
（1）Orthonormal Projection
我们遵循的标准立方体 the canonical cube [-1, 1]^3
把所有的物体都先放在平移和缩放到上面这个立方体内
How to do this?
平移+缩放
首先我们规定一个物体的六个边际 t b l r f n
然后再比例放大即可
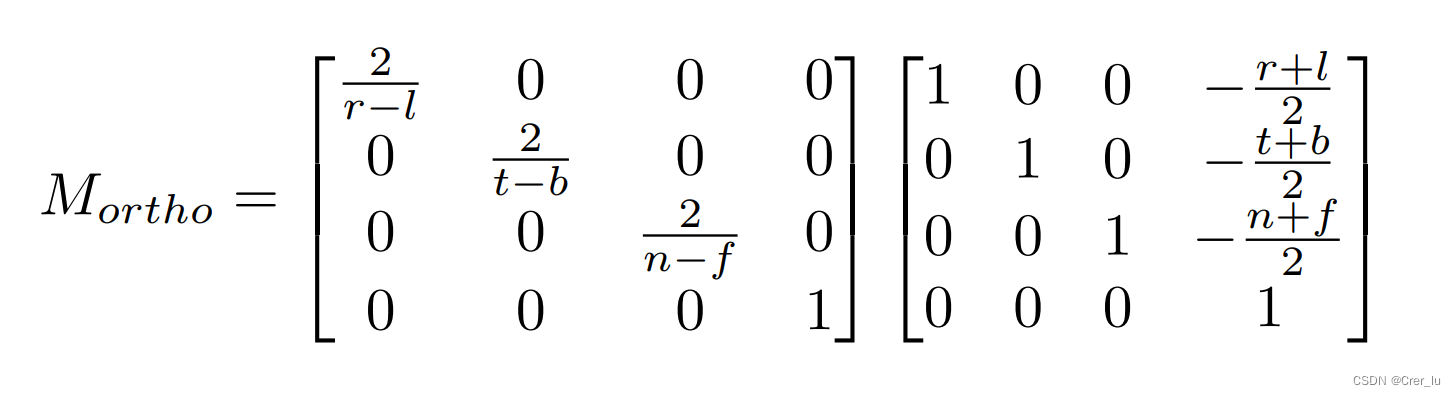
然后再look along -Z 并且观测的结果看不出远近关系
（但是透视投影就可以——近大远小）
（2）Perspective Projection
核心——相似图形的几何关系
How to do this？
挤压+正交投影（Orthonormal Projection）
挤压（squish）
把左边的z = f面给挤压到与 z = n面大小相等
有几点基本原则：
1.z = n上的点坐标不变
2.z = f的中心点坐标不变
3.z = f上的点z左边不变
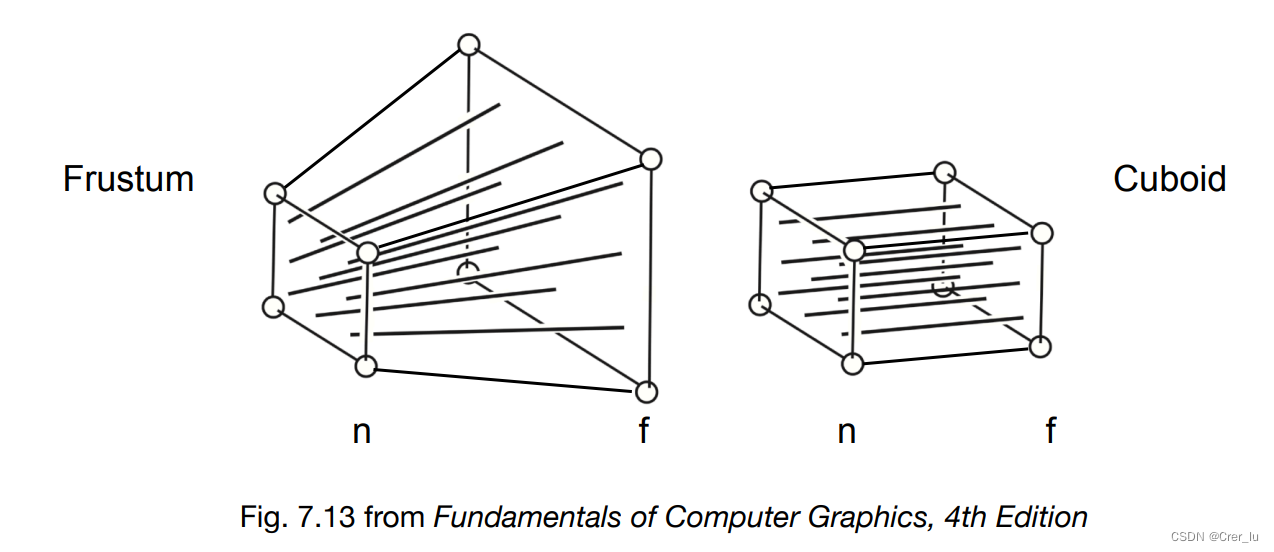
推导过程略 详见PPT内容
只要左乘一个如下矩阵
M
s
q
u
i
s
h
M_{squish}
Msquish即可
[ n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ] begin{bmatrix} n&0&0&0\ 0&n&0&0\ 0&0&n+f&-nf\ 0&0&1&0 end{bmatrix} ⎣⎢⎢⎡n0000n0000n+f100−nf0⎦⎥⎥⎤
闫老师最后提出一个问题：对于介于z = n与z = f之间的点的z坐标如何变化？
经过我的推导，应该是变小（即向z = f方向偏移）
推理方法：写出显式坐标，然后再列不等式求解
最后
以上就是妩媚身影为你收集整理的Games101-闫令琪 1-4讲 基础知识+变换 （笔记整理）Overview的全部内容，希望文章能够帮你解决Games101-闫令琪 1-4讲 基础知识+变换 （笔记整理）Overview所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复